Функция полезности сопоставляет каждому набору потребительских товаров некоторое число таким образом, что если набор А предпочтительнее набора В, то число, соответствующее набору А, будет выше, чем для В. Например, набор А на самой высокой из трех кривых безразличия Из может иметь уровень полезности 3, в то время как набор В на второй по высоте кривой И2 может иметь уровень полезности 2, а набор С на самой низкой кривой безразличия И)—уровень полезности 1. Следовательно, функция полезности дает ту же информацию о предпочтениях, что и карта безразличия. Как функции полезности, так и карты безразличия упорядочивают выбираемые потребителем наборы по уровням удовлетворения потребностей. [c.92]
Функции полезности легче применять к анализу выбора при трех и большем числе товаров просто потому, что в данном случае трудно начертить кривые безразличия. Однако при использовании функций полезности следует быть внимательным. Когда экономисты впервые изучали полезность, они надеялись, что индивидуальные предпочтения можно легко измерить в некоторой базисной шкале [c.92]
Имея в виду, что мы используем порядковые свойства функции полезности, мы можем теперь рассмотреть конкретную функцию. Функция U (F, С) = F говорит нам, что уровень удовлетворения потребностей, связанный с потреблением F единиц первого товара и С единиц второго товара, является произведением F . На рис. 3.16 показаны некоторые кривые безразличия, соответствующие данной функции. Чтобы начертить график, сначала выбираем конкретный набор, скажем F = 5 и С = 5, и определяем соответствующий уровень полезности 25. Затем строим кривую безразличия как совокупность всех наборов потребительских товаров и услуг, для которых F = 25 (например F=10, С =2,5 F=2,5, С =10). Вторая кривая безразличия содержит все наборы, для которых F = = 50, а третья — F = 100. [c.93]
Важным моментом является то, что числовые значения приписываются кривой безразличия только для удобства. Предположим, функция полезности изменилась, так что U (F ) = 4 F . Рассмотрим любой набор, который ранее давал уровень полезности 25, скажем, F = 5, С = 5. Теперь уровень полезности вырос за счет множителя 4 до 100. Таким образом, кривая безразличия, отмеченная числом 25, выглядит так же, но она должна быть помечена цифрой 100. Фактически единственная разница между кривыми безразличия, связанными с функцией полезности [c.93]
| Рис. 3.16. Графическое изображение функций полезности и кривых безразличия | 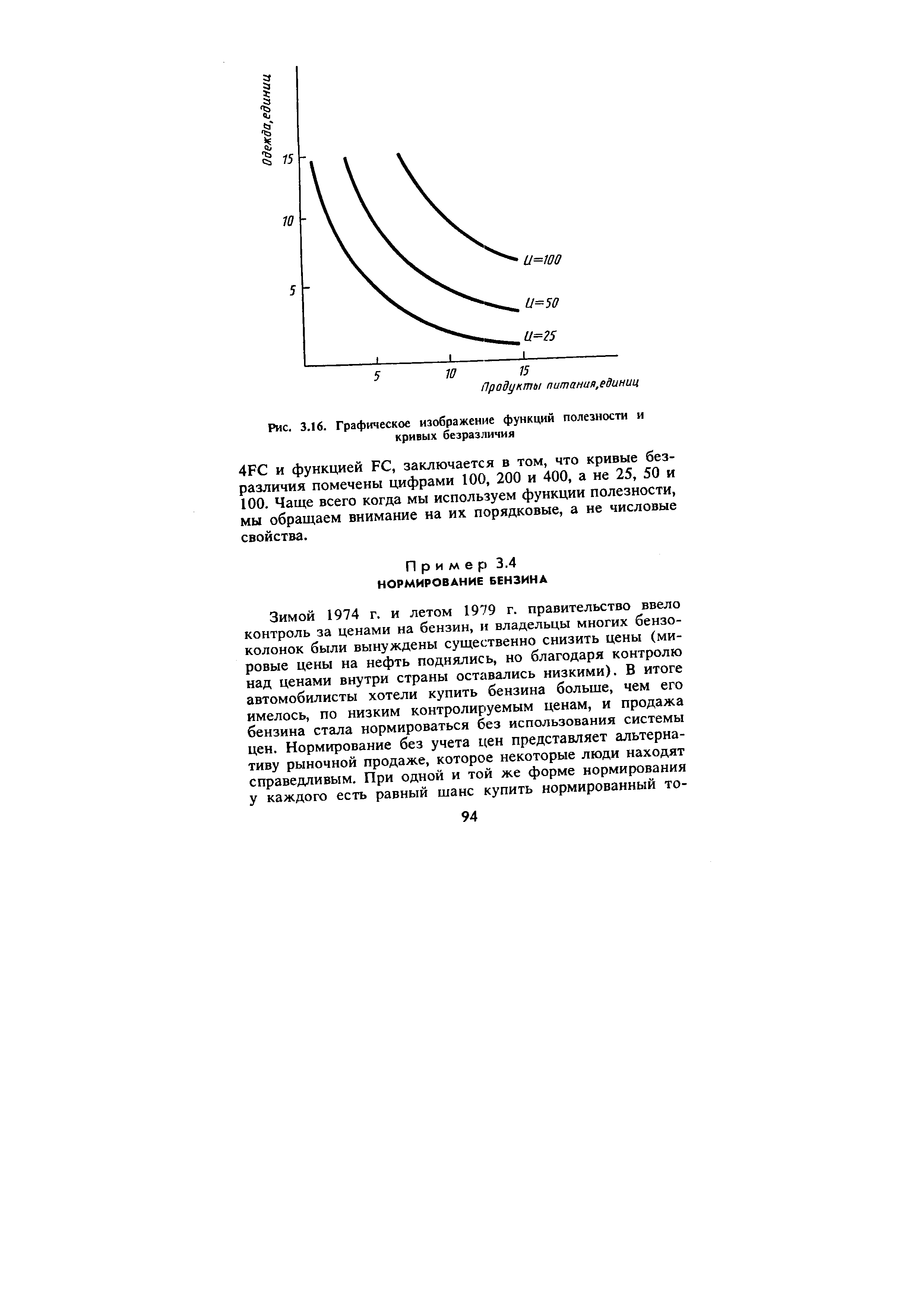 |
Бывают случаи, когда целесообразно использовать некоторые числовые свойства функции полезности. Одна из них возникает, когда люди осуществляют выбор в условиях риска, включающий сравнение полезности в двух различных временных точках. Другая ситуация, когда мы хотим проанализировать издержки и выгоды общественных проектов, для чего необходимо сопоставление полез-ностей разных индивидов. В данном разделе объясняется концепция предельной полезности и приведен пример того, как может быть сделан анализ потребительского выбора с использованием концепции интегральной и предельной полезности. [c.96]
Теория потребителя может быть представлена либо в терминах кривых безразличия, когда важны лишь порядковые свойства полезности (т. е. которые позволяют ранжировать альтернативы), или в терминах функции полезности. Функция полезности определяется путем присвоения числовой оценки каждому набору потребительских товаров и услуг. Если набор А предпочтительнее набора В, полезность набора А выше, чем В. [c.99]
Когда анализируется выбор в условиях риска или проводятся сравнения между отдельными индивидуумами, могут быть важны количественные свойства полезности. Функции полезности, которые мы изучаем, удовлетворяют принципу снижающейся предельной полезности чем больше потребляется товара, тем меньше приращение полезности. [c.99]
Если используется функция полезности и потребляется два товара, то полезность максимизируется, когда соотношение предельных полезностей двух товаров (которое является предельной нормой замещения) равно соотношению цен. [c.99]
| Рис. 5.За показывает, как можно изобразить отношение женщины-потребителя к риску. Кривая ОВ, задающая ее функцию полезности, указывает уровень полезности (на оси ординат), который может достигаться при каждом уровне дохода (отложенного в тысячах долларов на оси абсцисс). Уровень полезности растет с 10 до 16 и далее до 18 единиц по мере роста дохода с 10000 до 20 000 долл. и до 30 000 долл. При этом предельная полезность уменьшается, снижаясь с 10, когда доход растет с 0 до 10000 долл., до 6, когда доход увеличивается с 10000 до 20000 долл., и до 2 единиц, когда доход поднимается с 20 000 до 30 000 долл. |  |
Величина коэффициента значимости Д распространяется на весь интервал Кц - Kio. Но это правомерно лишь для линейных функций Г = f(K,). Рассмотрим для упрощения пример, когда функция полезности зависит от одного [c.49]
Налицо, хотя и небольшая, но явная погрешность расчета по формуле (3.21). При более сложных формах нелинейных функций полезности она может совершенно исказить действительную величину комплексного показателя. Избежать этого можно введением фактора нелинейности в формулу (3.21) в виде показателя степени ai при (К,-1)- Тогда [c.50]
В рассмотренном примере известны значения функции полезности бензина при различных сочетаниях его главных качественных свойств (табл.3. 4). Поэтому интегральный показатель качества данного продукта определен абсолютно точно прямым соотношением [c.53]
Он приведен только для того, чтобы прояснить необходимые условия математической корректности и содержательной эквивалентности прямого расчета Ки по формуле (3.23), и косвенного - по формулам (3.21), (3.27). Как оказалось, они очень деликатны. Достаточно небольшого их нарушения и косвенный расчет Кк утратит достоверность. Во-первых, истинные величины коэффициентов значимости единичных показателей /Я можно получить лишь из функции полезности. Во-вторых, даже для линейной формы [c.53]
Точное (совпадающее с индексом роста функции полезности) значение комплексного показателя уровня качества получается из формулы Б.А. Минина. Незначительную потребность дает формула средневзвешенной геометрической. Заметная ошибка характерна для среднеквадратической, и грубо ошибочен результат расчета по формуле среднеарифметической во всех её модификациях. [c.55]
Некоторые из приведенных формул дают хорошее приближение к истинной величине интегрального уровня качества при условии определения коэффициентов значимости единичных показателей на основе сопоставления базовой и итоговой функций полезности, как это было сделано в рассмотренных ранее примерах. Но проблема в том, что формальные способы синтеза Кк как раз и предназначены для тех случаев, когда функция полезности продукции неизвестна. Поэтому наиболее тяжелым и, в сущности, непреодолимым недостатком всех рассмотренных способов расчета Кк является необоснованность коэффициентов значимости ( Si) единичных показателей. [c.55]
Они определяют лишь гарантированную с вероятностью а меру расхождения с выборочной средней экспертной оценки значимости и генеральной экспертной средней. Проблема же оценки погрешности самой генеральной средней экспертной величины уровня значимости относительно его истинного значения лежит в совершенно иной плоскости. Она заключается в сопоставлении генеральной средней с реальным относительным приростом полезности продукта, обусловленным тем или иным относительным изменением соответствующего единичного показателя. Но это возвращает весь оценочный процесс к определению функции полезности продукции, без знания которой все суждения о величине pi остаются догадками. [c.59]
При этом нет необходимости применять какие-либо коэффициенты значимости единичных показателей качества и произвольные формулы их синтеза в обобщенный, поскольку этот синтез осуществлен автоматически в ходе интегрального расчета удельных функций полезности изделия (Кц). [c.69]
Как и в случае с электрической лампой, главные вопросы построения интегрального показателя качества холодильника заключаются в обосновании функции полезного эффекта за Т часов эксплуатации и функции совокупных затрат потребителя за этот же период времени. [c.75]
Аналитический этап. На данном этапе производится выделение и классификация функций объекта, выявление их взаимосвязи и соподчиненности, определение стоимости каждой из них. Стоимость функции равна затратам на создание её материального носителя. Например, стоимость функции генерирования энергии трактором определяется затратами на изготовление и монтаж его двигателя. Параллельно должна устанавливаться стоимостная оценка каждой функции в обеспечении суммарного эффекта потребления изделия. В данном пункте существует пока непреодоленная принципиальная трудность. Она заключена в отсутствии надежного теоретического основания для распределения полезности товара между отдельными функциями. Полезность, например, пропашного трактора — это общий объем пахоты за весь его жизненный цикл в га. Спрашивается, как разделить её между главными и второстепенными функциями его агрегатов двигателем, трансмиссией, ходовой частью, рамой, системой управления и т.д. Можно прибегнуть к проекции стоимости каждой функции на полезный эффект. Тогда доля функции в полезном эффекте будет равна её доли в стоимости изделия, которую рассчитать довольно легко. В этом есть вроде бы некоторый резон. Если изделие востребовано потребителем, то все затраты на его создание пропорциональны полезности этих затрат. Потребитель именно так распределяет свой бюджет, добиваясь равной предельной полезности на каждый затраченный рубль. Можно было бы признать эту логику, если бы не одно важное обстоятельство. ФСА как раз и предпринимается для того, чтобы выявить в составе функций узлов и деталей анализируемой конструкции излишние и бесполезные. Если же приписать им долю полезного эффекта, про- [c.134]
Рассмотрим карту поверхностей безразличия более подробно. Свойства этих поверхностей могут быть получены на основе соотношений (6.4). Будем для простоты считать, что функция полезности дифференцируема и имеет место соотношение [c.117]
Методы второй подгруппы состоят в построении единственного критерия (функции полезности ЛПР) или правила выбора решения до начала анализа множеств Gx и G . Эти методы близки к методам построения функции предпочтения, описанным в гл. 2, и отличаются лишь тем, что в данном случае предпочтения определяются не столько на основе наблюдений реального поведения ЛПР, сколько в диалоге с ним. Эти методы могут использоваться в таких задачах принятия решений, когда ЛПР — это единственный человек, к тому же очень хорошо понимающий свои предпочтения и умеющий их выразить. Они нашли свое применение в тех задачах, где ЛПР удовлетворяет этим требованиям. Обычно же вопросы, на которые должно ответить ЛПР, слишком трудны, что не позволяет использовать такие методы в большинстве задач, тем более в экономических задачах принятия решений с заранее неясными для ЛПР способами сочетания противоречивых критериев. , [c.301]
Особенностью этого метода является то, что целевая точка не обязательно должна быть недостижимой. Это и определяет в значительной степени вид функции полезности, которая в данном методе имеет вид [c.303]
Здесь p — параметр, не меньший размерности пространства критериев г, BI,. .., ег — положительные малые параметры. Чтобы представить себе смысл функции полезности (3.12), рассмотрим ее линии уровня (кривые безразличия) в пространстве критериев / при заданном значении / (рис. 6.6). [c.303]
Линии уровня этой функции в пространстве критериев / при заданной цели / приведены на рис. 6.6, а. Поскольку из-за малости величин EJ (/ = 1,. .., г) правое слагаемое практически не влияет на вид диний уровня, то получаем обычную функцию полезности [c.303]
Итак, функция полезности (3.12) является композицией функции полезности с заданными пропорциями и аддитивной функции полезности (3.14). При этом в случае цели, лежащей за пределами множества Gf, будет использоваться функция (3.12) если же цель лежит внутри множества Gf, то при достаточно больших значениях параметра р функция s(/, /) все более приближается к виду (3.14). Таким образом, при использовании функции (3.12) предполагается, что при недостижимой цели ЛПР заинтересован в максимальном приближении к ней с сохранением заданных ею пропорций, а в случае достижимой цели у него появляется возможность замещения отдельных критериев. [c.304]
Если функция полезности U(x) включает критерии аддитивно [c.308]
Методы выявления предпочтений ЛПР до рассмотрения множества допустимых решений обычно опираются на взвешивание различных критериев либо в виде (3.9) с априорным назначением весов, либо с помощью других методов свертывания критериев, рассмотренных ранее. При этом, конечно, критерии должны быть количественными целевыми функциями. Иногда используются-также методы диалогового построения функций полезности (или кривых безразличия). Отметим, что в рассматриваемых задачах заранее известны допустимые варианты решения, поэтому разумно использовать их и решать проблему выявления предпочтения одновременно с выбором решения задачи. Рассмотрим такие методы более подробно. [c.319]
Принципалу, однако, не всегда удается достичь наиболее желаемого результата посредством действий представителя. Другими словами, оптимизирующее поведение представителя не обязательно приводит к максимизации целевой функции принципала. Это может произойти по ряду причин. Во-первых, возможен конфликт интересов представителя и принципала в том смысле, что цель представителя (или функция полезности) может отличаться от цели принципала. В этом случае агент может стремиться максимизировать собственную полезность за счет полезности принципала. Во-вторых, сами действия агента или вытекающий из них результат могут быть неадекватны напри- [c.125]
Контроль правильности формирования корреспонденции счетов в некоторых системах выполняется не только в момент ввода информации о хозяйственной операции, но и независимо от него. Контроль выполняется в групповом режиме после окончания ввода всех записей, что позволяет локализовать большинство ошибочных и сомнительных проводок. Эта функция полезна при аудиторских проверках. Особенно важна она в системах класса бухгалтерский комплекс , где информация поступает в АРМ сводного учета из АРМ других участков учета и требует сплошной проверки. [c.165]
В координатах х, у для прямоугольника допустимых значений искомых неизвестных строятся линии равной выгодности. Для участника А это совокупность параллельных выпуклых функций, для участника В — это совокупность параллельных вогнутых функций. Точки возможных условий контракта — это точки касания функций полезности результата для участников. [c.114]
Все попытки определить функцию полезности на основе наблюдения за реакцией индивидуумов на вероятностные ситуации восходят к статье Бернулли о Санкт-Петербургском парадоксе (1737 г.). При объяснении этого парадокса Бернулли пришел к выводу, что рациональное поведение максимизирует не ожидаемый денежный выигрыш, а удовлетворение от этого выигрыша. Иначе говоря, потребитель руководствуется не математическим ожиданием , а моральным ожиданием успеха, при котором вероятность взвешивается по полезности дохода, зависящей, в свою очередь, от его абсолютного уровня. Предельная полезность дохода с каждым приростом последнего снижается, что заставляет потребителей настаивать на увеличивающихся выплатах, чтобы компенсировать риск потери никто не станет платить 1000 руб. за шанс выиграть 2000 руб. с вероятностью 50%. [c.58]
Позднее Дж. фон Нейман и О. Моргенштерн в фундаментальном труде Теория игр и экономическое поведение (1943 г.) дали формальное доказательство того, что принцип максимизации ожидаемой полезности является критерием рациональности ожидаемых решений. Они разработали систему аксиом количественной полезности, из которых следует существование такой функции полезности, математическое ожидание значений которой согласовано с предпочтениями субъекта. Иными словами, потребитель в состоянии определить, что предпочтительнее набор благ или лотерейный билет [c.58]
Карта изоквант представляет собой набор изоквант, каждая из которых показывает максимальный выпуск продукции, достигаемый при использовании определенных сочетаний факторов. Карта изоквант является альтернативным методом описания производственной функции, точно так же как карта кривых безразличия представляет собой один из способов описания функции полезности. Бесконечное число изоквант составляет изоквантную карту. Каждая изокванта ассоциируется с различным объемом выпуска продукции, и эти объемы возрастают по мере движения вверх и вправо по графику. [c.162]
Теперь обратимся к случаю нелинейной зависимости функции полезности F от качественного параметра Kf. ПриК ,= 1 F0=l+0,5 l°-5=l,5. [c.50]
Целесообразность такого усложнения устанавливается анализом фактического соотношения между КкнК,в тех случаях, когда известна функция полезности. Для иллюстрации в табл. 3.4 приведены данные о потребительском эффекте (полезности) автомобильного бензина с различными качественными характеристиками (содержанием серы (5), октановым числом (А), температурой конца кипения (Т)). [c.50]
В течение 1999г. появился ряд новых исследований, посвященных построению моделей роста с эндогенным технологическим прогрессом, где эффект масштаба в явном виде не присутствует. В частности, А.Юнг (Чикагский университет) предложил альтернативную модель, в которой размеры рынка и уровень затрат на НИОКР могут влиять не только на темпы роста, но и на функцию полезности нововведений для среднего потребителя (через расширение ассортимента предлагаемой на рынке продукции). [c.14]
Задача активизации роли государства особо актуальна с позиций общей теории социальной экономики, существования специфических интересов общества, которые не сводятся к интересам отдельных индивидуумов, т. е. функционально от них не зависят. Отсюда всякое благо может удовлетворять потребности качественно разных участников рыночных отношений, в т. ч. и несводимые потребности общества как такового способность блага удовлетворять несводимые потребности — социальные полезности. Несводимость последней к полезности для индивидуумов связана с тем, что в основе социальной полезности лежит несводимая общественная полезность, которая постулируется лишь для совокупности индивидуумов в целом. Именно независимость социальной полезности превращает государство в равноправного субъекта рынка. Все это имеет отношение к рациональному поведению государства. Можно напомнить в этой связи о невидимой руке , от которой мир ожидает достижения рыночной гармонии. Там, где потребности общества оказались сводимыми, где спрос на товары и услуги полностью растворялся в индивидуальных предпочтениях, там, действительно, рынок сумел ответить на все вопросы . Столкнувшись же с несводимыми общественными потребностями, с благами, имеющими социальную полезность, невидимая рука дала многочисленные сбои, породив на свет разного рода провалы рынка. Стало очевидным, что рука провидения не дотягивается до очень многих областей экономического пространства. Реакцией на это стало ограничение поля действия рыночных сил, замена их внерыночным регулированием ряда сфер экономического бытия. Эти ограничения можно преодолеть, если включить государство (носителя несводимых общественных потребностей) в число субъектов рынка. В общественной модели конкурентного рынка одновременно действуют и индивидуальные субъекты с присущими им интересами, и государство с его несводимыми потребностями. И первые, и вторые стремятся к максимизации собственной функции полезности, рука провидения мо- [c.209]
Отметим важное преимущество функции полезности (3.12) — ее использование позволяет свести задачу оптимизации (3.11) к задаче линейного программиро- Рис- 6>7> [c.305]
Чамберс одним из первых выявил значимость а) логической непротиворечивости используемых в теории идей и б) функции полезности учетной информации для принятия решений. Он писал [c.116]
Демски [24, с.626] ставит под вопрос адекватность неоклассической теории в качестве основы для исследования бухгалтерского учета. Он пишет, что неоклассическая теория несовершенна в вопросах динамики. Основное сомнение относительно PAT вызывает у него применимость присущего ей предположения о совершенстве рынков. На совершенном рынке предполагается, что каждый максимизирующий индивид обладает достаточным знанием корректных цен, объективных неценовых ограничений, собственной функции полезности для того, чтобы принять успешное решение, предшествующее реализации. Демски выражает мнение, что признание в PAT договорных и политических издержек практически свидетельствует об осознании несовершенства рынка [24, с.625—626]. [c.133]
Критерием, обеспечивающим сужение поля выбора портфеля инвесторов, являются кривые безразличия" [indifferen e urves]. В основе их построения лежат функции полезности инвестора, отражающие его отношение к риску и доходности портфеля. Принципиальный график формирования кривых безразличия инвестора, нейтрального к риску, представлен на рис. 11.4. [c.352]
Смотреть страницы где упоминается термин Функция полезности
: [c.93] [c.119] [c.303] [c.305] [c.308] [c.62]Смотреть главы в:
Цены и ценообразование в системе маркетинга -> Функция полезности
Популярный экономико-математический словарь -> Функция полезности
Экономико-математический словарь Изд.5 (2003) -- [ c.379 ]
Популярный экономико-математический словарь (1973) -- [ c.70 ]
Большая экономическая энциклопедия (2007) -- [ c.456 , c.472 , c.726 ]
Маркетинг (2002) -- [ c.883 ]
Микроэкономика глобальный подход (1996) -- [ c.76 , c.77 ]
