Если принять во внимание, что выработка рабочих колеблется в пределах (1 2) — (1 3), то при разных средних ее значениях крайние отклонения в выработке рабочих и выполнении норм от среднего их значения будут различными. Имея представление о теоретическом распределении вероятностей, можно получить и тео- [c.194]
| Рисунок 3.29. Соотношение фактического и теоретического распределения вероятности последовательных изменений фондового индекса DJ1 | 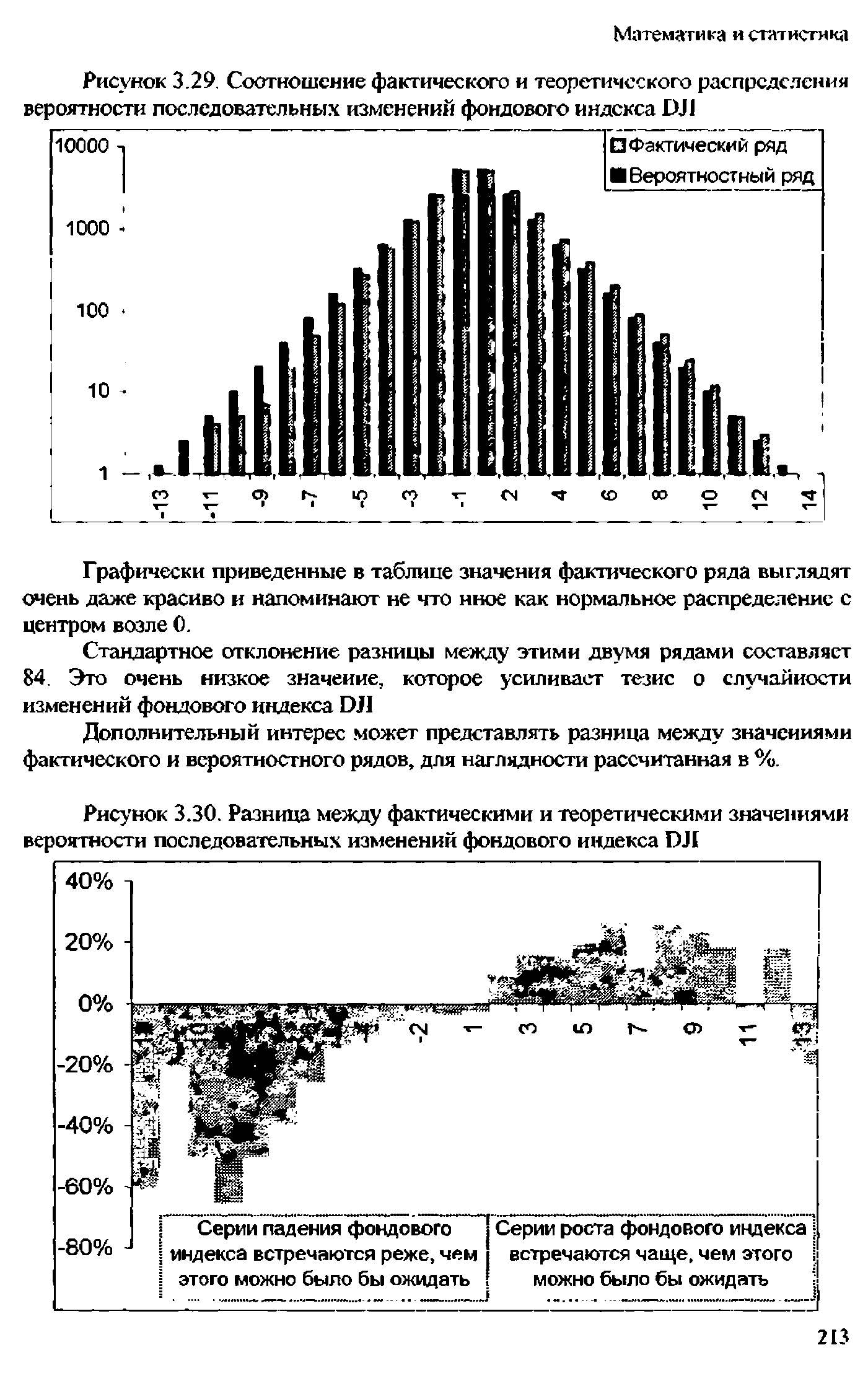 |
В предыдущих разделах мы познакомились с дискретным распределением вероятностей, когда рассматриваемая переменная могла принимать только определенные (дискретные) значения. Например такие переменные, как количество брака, количество поступающих пациентов и количество несчастных случаев, могут быть выражены только целыми числовыми значениями. В этом разделе мы рассмотрим непрерывное распределение, когда теоретически переменная может иметь любое значение в пределах заданного диапазона. [c.76]
Предложенный подход к построению оптимального портфеля тем не менее носит во многом теоретический характер, хотя мы и пытались отразить в наших представлениях портфеля рыночные реалии. При его использовании мы получаем континуальные комбинации опционов. Для решения проблемы континуума на практике достаточно будет интегралы заменить интегральными суммами, и в нашей задаче точками деления вещественной прямой надо будет выбрать именно рыночные страйки. Однако проблемы остаются. И связаны они с отсутствием полной и достоверной информации о рыночном распределении вероятностей будущей цены базового актива. К решению подобных проблем мы и переходим. [c.18]
Проверка статистических гипотез о виде распределения случайных величин. При построении математической модели исследуемых процессов часто возникают задачи сопоставления полученного материала экспериментов с известными теоретическими распределениями. Если сопоставить вероятность попадания в интервалы, на которые разбита выборка, с соответствующими частотами, полученными из наблюдений, или проводить графическое сравнение полигонов и гистограмм с некоторой теоретической функцией распределения, то можно получить представление о степени близости теоретического и эмпирического распределений. [c.72]
Нормальное распределение — вид теоретического распределения переменных (функция вероятности результата). Наблюдается при изменении переменной под влиянием множества независимых факторов. [c.403]
Распределения вероятности времени выполнения отдельных этапов цикла, а также всего цикла представлены на рис. 71. Как видим, каждый из этапов, теоретически, может быть выполнен в весьма сжатые сроки. Однако в тра- [c.256]
Характерными примерами теоретического уровня представления задач в области качества являются законы распределения вероятных величин показателей качества, зависимости цены от качества и объема продаж, модели систем качества и т. п. [c.399]
Иногда по виду гистограммы можно с большой уверенностью заключить, что результат измерения подчиняется (или не подчиняется) нормальному закону распределения вероятности. Если, например, гистограмма имеет вид, показанный на рис. 41, а, то результат измерения определенно не подчиняется нормальному закону. Если же гистограмма имеет вид, показанный на рис. 41, б, то возникает сомнение достаточно ли хорошо она соответствует теоретической кривой нормального закона распределения плотности вероятности, показанной пунктиром Для разрешения этого сомнения нужно иметь правило, руководствуясь которым можно было бы принимать то или иное решение. [c.104]
Существует несколько так называемых критериев согласия, по которым проверяются гипотезы о соответствии экспериментальных данных тому или иному закону распределения вероятности результата измерения. Наиболее распространенным из них является критерий К. Пирсона. При использовании этого критерия за меру расхождения экспериментальных данных с теоретическим законом распределения вероятности результата измерения принимается сумма квадратов отклонения частостей mjn от теоретической вероятности Р попадания отдельного значения результата измерения в /-и интервал, причем каждое слагаемое берется с коэффициентом п/Р [c.105]
Если расхождение случайно, то х2 подчиняется х2 -распределению (хи- квадрат распределению К. Пирсона). Кривые интегральной функции этого распределения представлены на рис. 42. Интегральная функция определяет вероятность того, что случайное число примет значение, меньшее аргумента этой функции. Поэтому, задавшись значением интегральной функции распределения К. Пирсона F(XO), можно проверить, больше или меньше ее аргумента х (см- Рис- 42) вычисленное значение X2- Если меньше, то с выбранной вероятностью х2 можно считать случайным числом, подчиняющимся х2-распределению К. Пирсона, т. е. признать случайным расхождение между эмпирической и теоретической плотностью распределения вероятности результата измерения. Если же окажется, что х2 > Хо. то с той же вероятностью придется признать, что х2 не подчиняется распределению К. Пирсона, т. е. гипотеза о соответствии эмпирического закона распределения вероятности теоретическому не подтверждается. [c.105]
Теоретическая вероятность PJ попадания в /-и интервал отдельного значения результата измерения, подчиняющегося нормальному закону распределения вероятности, очевидно равна [c.108]
Графически оно показано на рис. 57. Вероятность удвоенных по сравнению с г значений остается прежней. Оценки числовых характеристик теоретической модели эмпирического распределения вероятности, представленного табл. 17, [c.144]
Оценки числовых характеристик теоретической модели этого распределения вероятности [c.146]
Если результат измерения А задан теоретической моделью эмпирического закона распределения вероятности, то используется то, что интегральная функция распределения вероятности F(0 представляет собой вероятность того, что [c.147]
По специальной таблице, приводимой в курсах по теории вероятностей для X и г, определяем вероятность приближений опытной кривой к теоретическому распределению. Эта вероятность равна Р=0,19. Следовательно, гипотезу о распределении интервалов прибытия поездов на станцию по закону Эрланга можно считать правдоподобной. [c.55]
Наибольший интерес в финансовых активах для нас представляет цена. Однако в анализе цен финансовых активов мало пользы от распределения вероятностей, поскольку поведение цен не имеет тенденции быть стационарным. Причина может быть в том, что со временем цены активов изменяются все вместе, например, цены акций со временем растут. Таким образом, математическое ожидание и среднее квадратическое отклонение цен обычно будут выше в данном году, чем в предыдущем. Более того, цены активов могут теоретически возрастать до бесконечности, но не могут упасть ниже нуля, и поскольку цены растут, то будет наблюдаться тенденция правосторонней скошенности распределения цен. [c.190]
Число событий Наблюдаемая частота Наблю-, лаемая вероятность Теоретическая вероятность Наблюдаемое распределение Теоретическое распределение Абсолютная разность [c.21]
Формула, определяющая теоретическую плотность вероятности погрешности измерения Д, распределенной по нормальному закону, имеет вид [c.52]
Если искомая вероятность окажется очень малой, практически меньше 0,1, то выбранное теоретическое распределение следует считать неудачным. При относительно большом значении искомой вероятности теоретическое распределение можно признать не противоречащим опытным данным. [c.36]
Первый этап в процессе определения подходящего закона распределения вероятностей - визуальное сравнение полученной гистограммы с известными теоретическими кривыми (равномерное распределение, нормальное распределение, распределение Пуассона, экспоненциальное распределение, гамма-распределение и т.д.). Однако такое визуальное распределение позволяет лишь сделать предположение о характере распределения и никогда не дает достаточных оснований, чтобы окончательно принять некоторую гипотезу о виде теоретического распределения. [c.91]
Кроме рассмотренных выше дискретных случайных величин существуют случайные величины с иными типами распределения вероятностей. Наиболее часто используются непрерывные случайные величины. Они могут принимать бесконечное множество значений, часто считается, что теоретически значение может быть любым числом из заданного промежутка или всей числовой прямой. Как и для любой случайной величины, функция распределения, задаваемая равенством F(x) = Р(Х < ж), полностью определяет непрерывную случайную величину. Специфика непрерывных случайных величин состоит в том, что функция F(x) для них предполагается непрерывно дифференцируемой на всей числовой прямой (иногда накладывают несколько более слабые условия). [c.8]
Пусть проведено п наблюдений за объектом исследований. Эти наблюдения в системе координат (Xi,X2,...,Xn) будут представлять собой точки, которые образуют корреляционное поле объекта. Теоретически это поле можно представить, как л-выборку из генеральной совокупности, образованной случайным вектором X с распределением вероятностей имеющих нулевые средние и ковариационную матрицу ov(Xj, Xj) и дисперсии [c.83]
Теоретический анализ, опирающийся на специальные раз-теории вероятностей, а также серия поставленных на ЭВМ вычислительных экспериментов показали, что только узкое семейство вероятностных распределений, простейшим из которых является распределение Парето, при О 1, надежно обеспечивает концентрацию > 75% промышленных запасов нефти менее чем в 1О% месторождений. Именно такие цифры и закономерности характерны для подавляющего большинства нефтегазоносных бассейнов и мира [l] [c.82]
Ещ г одним примером подобной абстракции является обоснование возможности использования регрессионных моделей в экономическом и финансовом анализе. Принципы моделирования с помощью регрессионных зависимостей в теоретическом плане разработаны в рамках теории вероятностей и математической статистики в частности, там предполагается случайность выборки, независимость ее элементов, нормальность распределения и т.д. Эти условия на практике выполнены далеко не всегда. [c.62]
Здесь вместо математического ожидания и дисперсии случайной величины взяты ее статистические моменты. Назовем закон распределения случайной величины Я, заданной плотностью /(Я) теоретическим. Зная, закон распределения, можно найти теоретические вероятности попадания в каждый из ин- [c.197]
Опционом колл со страйком Е называют инструмент С(Е) с платежной функцией с(х Е) = тах(0, х—Е), а опционом пут - инструмент Р(Е) с платежной функцией р(х Е) = тах(0, Е-х). В начале периода цена базового актива равна ц0- Цена актива в конце периода является случайной величиной с плотностью вероятности Дх) и функцией распределения F(x), которым соответствует среднее ц. В теоретической конструкции нам будет удобно допускать и отрицательные значения этой случайной величины (с малой вероятностью). Безрисковый относительный доход принимается равным г (т.е. безрисковая доходность равна г - 1). Будем считать рынок нейтральным к риску, и потому должно быть ц = г ц0- [c.5]
Ситуация существенным образом усложняется, если в качестве меры рассеяния ожидаемого дохода портфеля необходимо указать квантильное отклонение с заданной доверительной вероятностью, так как это невозможно сделать, если неизвестен закон распределения доходов портфеля. Теоретически, закон распределения доходов портфеля можно найти, если известны законы распределения доходов входящих в него активов. Однако на практике аналитическое решение такой задачи сопряжено со значительными трудностями даже для малого числа активов (за исключением некоторых частных случаев). Это происходит потому, что, во-первых, доходы по входящим в портфель активам могут быть коррелированны между собой, во-вторых, при суммировании доходов активов законы их распределения могут существенным образом деформироваться, поэтому распределение дохода портфеля может сильно отличаться от распределений доходов составляющих его активов. [c.236]
Данная глава посвящена моделированию фактического распределения сделок с помощью регулируемого распределения, то есть поиску функции и ее подходящих параметров, которые моделируют фактическую функцию плотности вероятности торговых P L с двумя точками перегиба. Вы можете использовать уже известные функции и методы, например, полиномиальную интерполяцию или экстраполяцию, интерполяцию и экстраполяцию рациональной функции (частные многочленов), или использовать сплайн-интерполяцию. После того как теоретическая функция найдена, можно определить ассоциированные вероятности тем же методом расчета интеграла, который использовался при поиске ассоциированных вероятностей регулируемого распределения, или рассчитать интеграл с помощью методов математического анализа. Одна из целей этой книги — позволить трейдерам, использующим немеханические системы, применять те же методы управления счетом, что и трейдерам, использующим механические системы. Регулируемое распределение требует расчета параметров, они относятся к первым четырем моментам распределения. Именно эти моменты — расположение, масштаб, асимметрия и эксцесс — описывают распределение. Таким образом, кто-либо, торгующий по немеханическому методу, например по волнам Эллиотта, [c.141]
Пусть Р. есть вероятность для х при заданном распределении F(x) принять значение, принадлежащее /-тому интервалу. Тогда теоретическое значение частоты в этом интервале будет определяться, как от/т = рр, где п — объем выборки. [c.73]
Полученное эмпирическое распределение сравнивается с теоретическим, т. е. равномерным в правильной кости вероятность выпадения каждого числа очков должна быть равна 1/6, при 600 бросках это даст по 100 выпадений каждого числа очков. С помощью критерия х2 проверяется нулевая гипотеза о том, что различия эмпири ческого и теоретического распределений случайны, т. е. не являются систематическим результатом фальсификации формы кости или положения центра тяжести в ней Н0 / к№1 -fini.,,p- Результаты испытания и расчет %2 приводятся в табл. 7.6. [c.202]
Расчетно-аншштические методы построения кривой распределения вероятностей потерь и оценки на этой основе показателей предпринимательского риска базируются на теоретических представлениях. К сожалению, прикладная теория риска хорошо разработана только применительно к страховому и игровому рискам. Элементы теории игр в принципе применимы ко всем видам предпринимательского риска, но прикладные математические методы оценочных расчетов производственного, коммерческого, финансового рисков на основе теории игр пока не созданы. [c.182]
Для определения степени согласованности эмпирического и теоретического распределений предложены различные критерии согласия. Так, известны критерий согласия Пирсона, Романовского, Колмогорова, Ястремского. Критерий согласия Пирсона сводится к исчислению по распределению Пирсона вероятности достижения л 2 данного значения Р = х2. При этом х2 рассчитывается по формуле (9.3) [c.189]
РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ (в математической статистике) [probability distribution] — ряд чисел, показывающих, как часто встречается то или иное значение случайной величины, или соответствующая таблица, диаграмма или математическая формула, их заменяющая. Различают эмпирические Р.в., получаемые в результате экспериментов и измерений, и теоретические Р.в. (к которым бывает удобно с той или иной точностью приводить эмпирические Р.в.) Если, напр., при обработке результатов наблюдения получены некоторые число- [c.300]
Если это условие соблюдается, то дполнительно проверяются, ,хвосты" теоретического и эмпирического законов распределения вероятности. При 10 < п < 20 считается допустимым отклонение одного из независимых значений результата измерения Qf от среднего арифметического больше чем на 2,5 SQ, при 20 < и < 50 — двух, что соответствует доверительной вероятности Р 0,98. [c.110]
Если результаты измерений А, В,. . . заданы теоретическими моделями змпирических законов распределения вероятности, то следует опять-таки зоспользоваться тем, что интегральная функция распределения вероятности F (0 представляет собой вероятность того, что [c.158]
Табл. 11.2. позволяет вычислить числовое значение (меру) для разницы между результатами, полученными экспериментально, и ожидаемыми или теоретическими значениями. Распределения хи-квадрат представляют собой семейство кривых, зависящих от степеней свободы (v). Они сильно скошены для малых степеней свободы, но приближаются к кривым нормального распределения с возрастанием и. Значение %2 = 6,309, вычисленное из модели теоретического распределения и экспериментального распределения, может быть сопоставлено со значениями, приводимыми в соответствующих таблицах1 для того, чтобы решить вопрос о значимости. Таблица дает критерии значимости для вероятностей осуществления 1 на 1000 до почти полной достоверности. Последние построены так, что по ним можно судить о степени согласия между ожидаемыми и наблюденными значениями. Если согласие слишком хорошее, то результаты могут считаться подозрительными и возможно, что они состряпаны . Обычно рассматриваемые значения бывают значимы на 5%, 1% или 0,1%-ном уровнях. Значения хи-квадрат при одной, двух, трех, четырех и пяти степенях свободы для 5%-ного уровня значимости составляют соответственно 3,84 5,97 7,82 9,94 11,07 и 12,59. Возьмем для примера случай, когда имеются три степени свободы и значение %2 для вероятности р = 0,05 составляет 7,82 а экспериментальное значение %2 составило 6,309. Поскольку это последнее лежит в пределах 7,82, можно заключить, что экспериментальное распределение числа отказов в фиксированных промежутках времени, при котором число отказов за фиксированный интервал времени могло превысить 50 случаев на 1000, не является достаточно значимым. [c.179]
Часто ошибочно полагают, что использование каких-то отдельных характеристик распределения вероятностей результата очень просто устраняет трудность выбора наилучшего решения. Например, чаще всего используют математическое ожидание результата, иногда — дисперсию. Однако, как показывает практика, выбор на основе таких характеристик не всегда согласуется с личными представлениями ЛПР о наилучшей альтернативе. В частности, это объясняется также и тем, что, описывая задачи с риском, ЛПР редко использует такие теоретические понятия, как "распределение вероятностей", "случайная величина", "квантиль" и т. п. Вместо них человек обычно оперирует такими малоформализуемыми понятиями, как "шансы на выигрыш", "возможность неудачи", "тяжесть последствий" и др. Он их воспринимает как более привычные, а потому — и более надежные. Хотелось бы, чтобы правила выбора также использовали подобные простые и понятные ЛПР суждения чтобы на основе таких суждений можно было отыскивать сначала эффективные, а при необходимости — и наилучшие альтернативы. [c.220]
