Теперь рассмотрим случай оптимизационного исследования. Пусть существует единственный критерий функционирования системы U (st, s2) скажем, среднее за весь период планирования потребление с в расчете на душу населения. Надо найти с помощью имитационных экспериментов оптимальный вариант управлений sx и s2. Это можно сделать с помощью различных градиентных методов поиска экстремума функции U (s1 s2), причем построение градиента функции U (sb s2) основывается на экспериментальном подсчете значений этой функции в нескольких точках (SL s2). В теории планирования эксперимента разработаны методы разумного выбора таких точек. [c.286]
На основании необходимого условия экстремума функции двух переменных S=S(bo, 0 (3.4) приравниваем к нулю ее частные производные, т. е. [c.54]
На основании необходимого условия экстремума функции нескольких переменных S(bo, b, ..., bp), представляющей (4.3), необходимо приравнять нулю частные производные по этим переменным или в матричной форме — вектор частных производных [c.84]
Всякое решение системы определяет точку х = (х°,х2,...,х°), в которой может иметь место экстремум функции f x1,x2,...,xn). Следовательно, решив систему уравнений, получим все точки, в которых функция Лагранжа может иметь экстремальные значения. [c.120]
Необходимо найти такое значение х, при котором величина T/j была бы минимальной. Воспользуемся известным правилом нахождения экстремума функции [c.13]
Безусловный экстремум функции 424 [c.460]
Поскольку экстремум функции х Ах/х х может достигаться (достаточно выбрать в качестве х собственный вектор, соответствующий AI или Ап), из теоремы 4 следует, что можно определить AI и Ап следующим образом [c.261]
Те значения аргумента, при которых достигаются экстремумы функции, называются точками экстремума функции. [c.144]
V Пример 2. Исследовать на экстремум функцию /(ж) = = ж3-3ж. [c.148]
| Рис. 9.6. Экстремум функции в стационарной точке XQ | 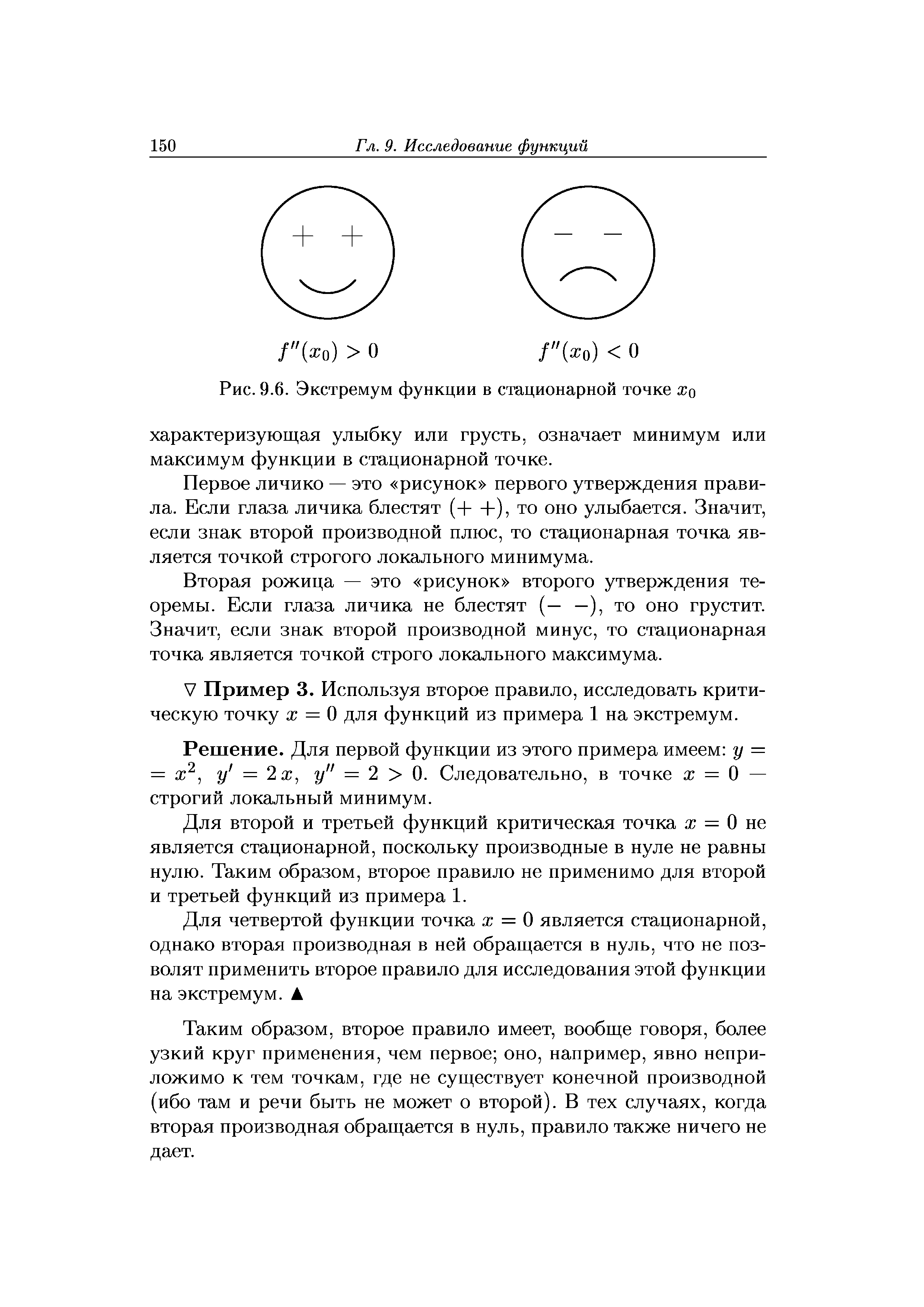 |
Экстремум функции двух переменных [c.305]
| Рис. 15.1. Экстремум функции двух переменных | 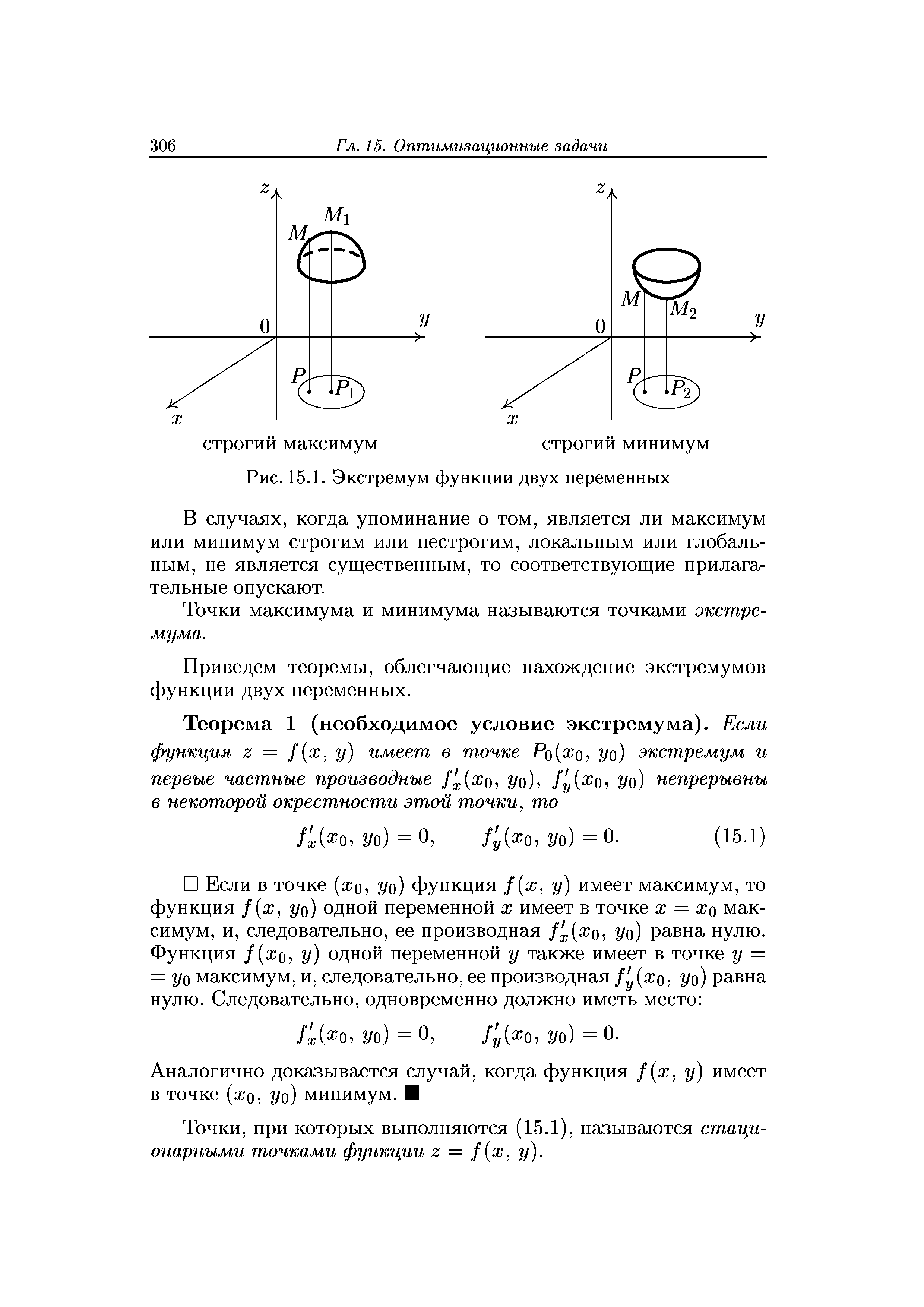 |
Заметим, что точки экстремума могут быть не только в тех точках, в которых частные производные функции равны нулю. Экстремум функции может быть и в тех точках, где хотя бы одна из частных производных не существует или равна бесконечности. На рис. 15.2 изображена функция с конусообразным графиком. В вершине конуса — точке MI — находится максимальная точка функции, однако частные производные там не существуют (в соответствующей точке невозможно провести касательную плоскость). [c.307]
V Пример 1. Найти экстремум функции z = 2х + 8-х2 -22. [c.308]
V Пример 2. Найти экстремум функции [c.309]
Экстремум функции многих переменных [c.310]
Достаточные условия экстремума функции можно сформулировать и на языке квадратичной формы, изучаемой в разделе Аналитическая геометрия и линейная алгебра . Достаточные условия экстремума функции многих (и не только двух) переменных сводятся к положительной (или отрицательной) определенности квадратичной формы [c.310]
Затем производим итерации с малым шагом . При малом шаге используется идея процедуры Кифера — Вольфовица, смысл которой состоит в следующем. Известно, что для нахождения экстремума функции / (х), непрерывно дифференцируемой в области задания и имеющей экстремум в точке X=XQ, можно использовать градиентный метод, описываемый рекуррентным соотношением [c.48]
Многомерным аналогом процедуры Кифера — Вольфовица для нахождения экстремума функции многих переменных f(x) = = f(x, х2,..., хп) является процедура, описываемая следующим рекуррентным соотношением, [c.49]
Обобщение результата, полученного Кифером —Вольфови-цем, показал, что если относительно функций V f xn и 0 [п+1,, хп, ш] имеются лишь некоторые априорные сведения общего характера, то процедура, олисанная соотношением (4), при выполнении некоторых условий может быть использована для отыскания экстремумов функции. Используя указанную процедуру, можно записать соотношение для отыскания последовательных приближений экстремальной точки [c.49]
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [mathemati al programming] (см. также Оптимачьное программирование) — раздел математики, который "... изучает методы решения задач на нахождение экстремума функций (показателя качества решения) при ограничениях в форме уравнений и неравенств"40. Оно объединяет различные математические методы и дисциплины исследования операций линейное программирование, нелинейное программирование, динамическое программирование, выпуклое программирование, геометрическое программирование, целочисленное программирование и др. [c.186]
ОПТИМИЗАЦИЯ [optimization] — 1. Процесс нахождения экстремума функции, т.е. выбор наилучшего варианта из множества возможных, процесс выработки оптимальных решений. [c.247]
ОПТИМУМ, ОПТИМАЛЬНОСТЬ [optimum, optimality] — с точки зрения математики, оптимум функции есть такое ее экстремальное значение (см. Экстремум функции), которое либо больше других значений той же функции (тогда это глобальный или, лучше, абсолютный максимум), либо меньше других значений — тогда это глобальный (абсолютный) минимум. Если трактовать наибольшее или наименьшее значение каких-то экономических характеристик как наилучшее (в [c.248]
Экономический смысл предельных величин состоит в том, что их можно использовать для принятия оптимальных решений с помощью методов дифференциального исчисления. Тогда, в частности, нахождение оптимума основывается на элементарных правилах если при анализе функции первая производная равна нулю, это означает экстремум функции и, следовательно, возможный ее оптимум. Требуется, однако, дополнительный анализ для выяснения единственности данной экстремальной точки, а также характера ее экстремальности является она максимумом или минимумом функции. Кроме того, оптимум совпадает с экстремальной точкой не во всех случаях. В частности, указанное правило не пригодно, когда точка оптимума находится на границе области допустимых решений (см. рис. О. 9 к ст. "Оптимум, оптимальность"). [c.276]
ЭКСТРЕМУМ ФУНКЦИИ [extremum] — термин, объединяющий понятия максимума к минимума функции. На простейшем примере функции одной переменной можно пояснить эти исключительно важные для экономики математические понятия (рис. Э.4). [c.424]
Весовые коэффициенты ja и 7 соответствуют доле общего времени цикла, в течение которой раствор вступает в контакт с источником в абсорбере и десорбере соответственно. Задача (5.119), (5.120) путем преобразований сводится к поиску экстремума функции двух переменных — nd и qd [c.206]
В общем виде математическое программирование — это совокупность методов, позволяющих определять условный экстремум функции многих переменных при наличии ограничений, т.е. тогда, когда нет уверенности в возможности ис— полыювшшя классических методов. [c.143]
Наличие локального экстремума функции при некотором значении аргумента нисколько не зависит от того, как ведет себя функция вдали от этого значения. С этой точки зрения понятно, что строгий локальный минимум функции может быть больше строгого локального максимума, — подобно тому как впадина в горах может быть выше, чем небольшая вершина. В отличие от строгого локального максимума (минимума) существует еще понятие строгого глобального максимума (минимума] на некотором множестве. Естесственно, что строгий глобальный максимум больше всех остальных значений значений функции на данном множестве (в том числе и дальних), а строгий глобальный минимум — меньше. В географических горных терминах строгий [c.143]
Смотреть страницы где упоминается термин Экстремум функции
: [c.48] [c.92] [c.22] [c.176] [c.182] [c.198] [c.249] [c.493] [c.497] [c.499] [c.142] [c.143] [c.145]Смотреть главы в:
Математика для социологов и экономистов Учебное пособие -> Экстремум функции
Справочник по математике для экономистов -> Экстремум функции
