| Рис. 8. Экономически эффективные границы эксплуатации сильнообводненных скважин |  |
На рис. 3.20 представлена связь сбора зерновых в первой зоне (показатель /4) и падения уровня воды>в озере (показатель /е, измеряется в метрах). На рисунке приведены лишь эффективные границы множества достижимых значений /4 и /6 при пяти [c.231]
Использование представления G/ в геометрическом виде на экране ЭВМ делает анализ множества Gf простым и удобным для ЛПР. Поскольку эффективное множество Pf является границей множества G/, то вместе с пониманием геометрии множества Gf ЛПР начинает понимать и геометрию множества Pf. Отметим, что знание всего множества G/ может иметь и самостоятельную ценность ведь предположение о том, что ЛПР заинтересована в постоянном увеличении критериев /ив выходе на эффективную границу, является лишь абстракцией — в реальности ЛПР может быть заинтересовано в создании некоторого резерва , что выразится в выборе внутренней точки множества G/, близкой к эффективному множеству. Если же ЛПР действительно заинтересовано в выходе на множество Pf, то на основе множества G/ можно легко построить другое множество, имеющее более простую геометрию, но ту же самую эффективную границу. [c.315]
Рассмотрим некоторую произвольную точку X, У), принадлежащую эффективной границе множества G. Решим задачу оптимизации (1.2) — (1.4) с У=У и найдем ее решения у( и xt (i = 1,. . ., и), а также множитель Лагранжа v. Очевидно, что [c.343]
У не лежала бы на эффективной границе G. Как было показано в этом параграфе ранее, назначив цены р и q такими, что p/q = v, мы сделаем план затрат и выпуска ,, yt выгодным для каждого из предприятий. Таким образом, проблема выбора стимулирующего механизма с ценами на ресурсы и продукцию, одинаковыми для всех предприятий, может быть решена в рассматриваемой системе, если выбранные каким-то образом значения X, У лежат на эффективной границе множества их достижимых значений. Как мы увидим в дальнейшем, это свойство сохраняется и для более сложных экономических систем. [c.343]
| Рисунок 1-8 Эффективная граница | 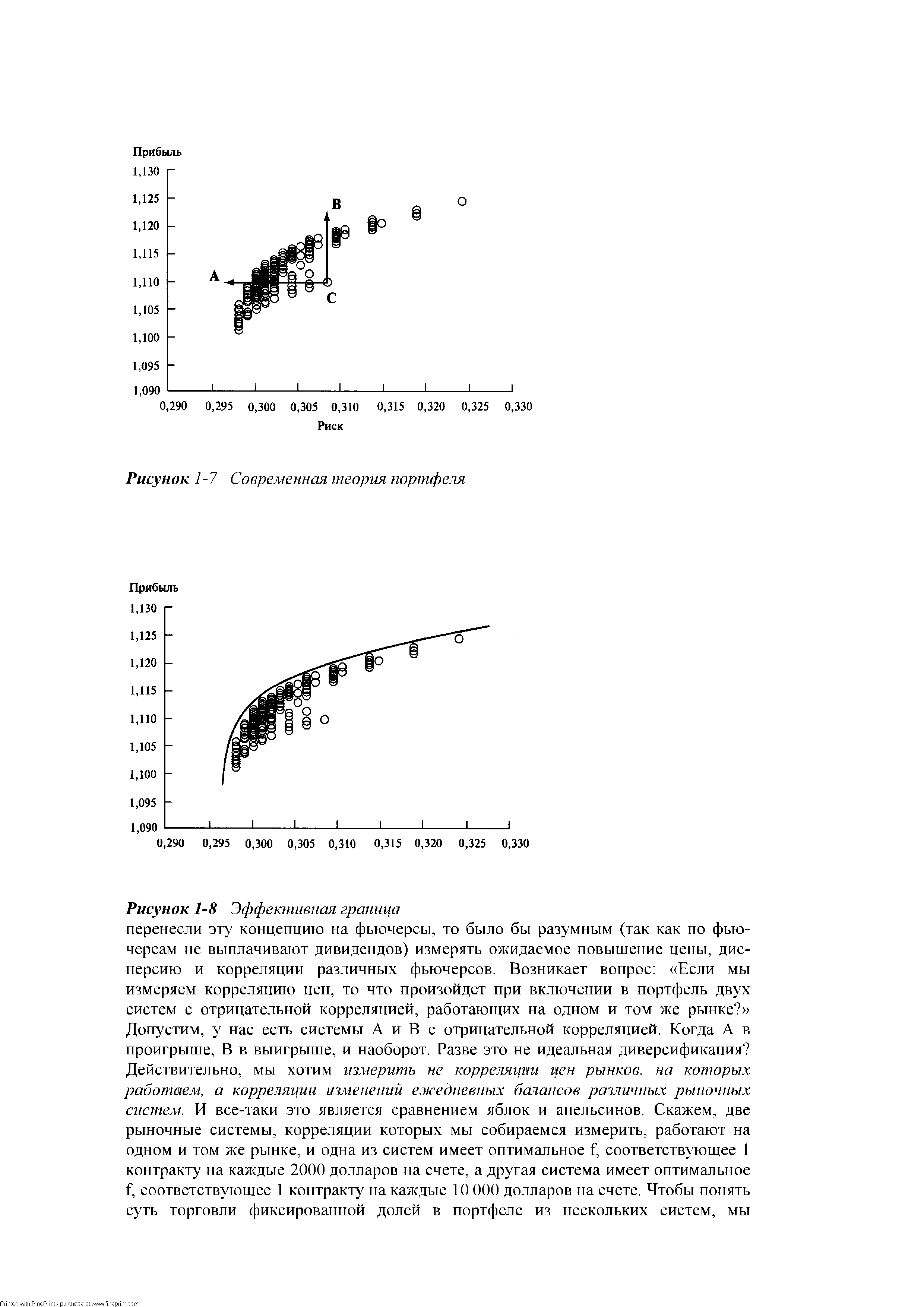 |
В уравнении (7.Ola) формула внутри скобок ( ) представляет собой отношение Шарпа. Отношение Шарпа для портфеля — это отношение ожидаемых избыточных значений прибыли к стандартному отклонению. Портфель с наибольшим отношением Шарпа является портфелем, где линия ML касается эффективной границы при данном значении RFR. [c.203]
Проведем данный расчет для каждой точки на эффективной границе. Максимальное значение уравнения (7.Ola) 0,502265 соответствует координатам (1,03 0,02986), они задают точку, которая соответствует точке В на рисунке 7-1, где линия ML касается эффективной границы. Точка касания соответствует определенному портфелю на эффективной границе. Отношение Шарпа определяет наклон ML, причем самым крутым наклоном обладает касательная к эффективной границе. [c.203]
Эффективная граница Линия ML [c.203]
Геометрическая эффективная граница [c.206]
Особенность рисунка 7-1 состоит в том, что он отображает арифметическое среднее HPR. Если прибыли реинвестируются, то для координаты эффективной границы по оси Y правильнее рассматривать геометрическое среднее HPR. Такой подход многое меняет. Формула для преобразования точки на эффективной границе из арифметического HPR в геометрическое такова [c.206]
| Рисунок 7-2 Эффективная граница с реинвестированием и без реинвестирования | 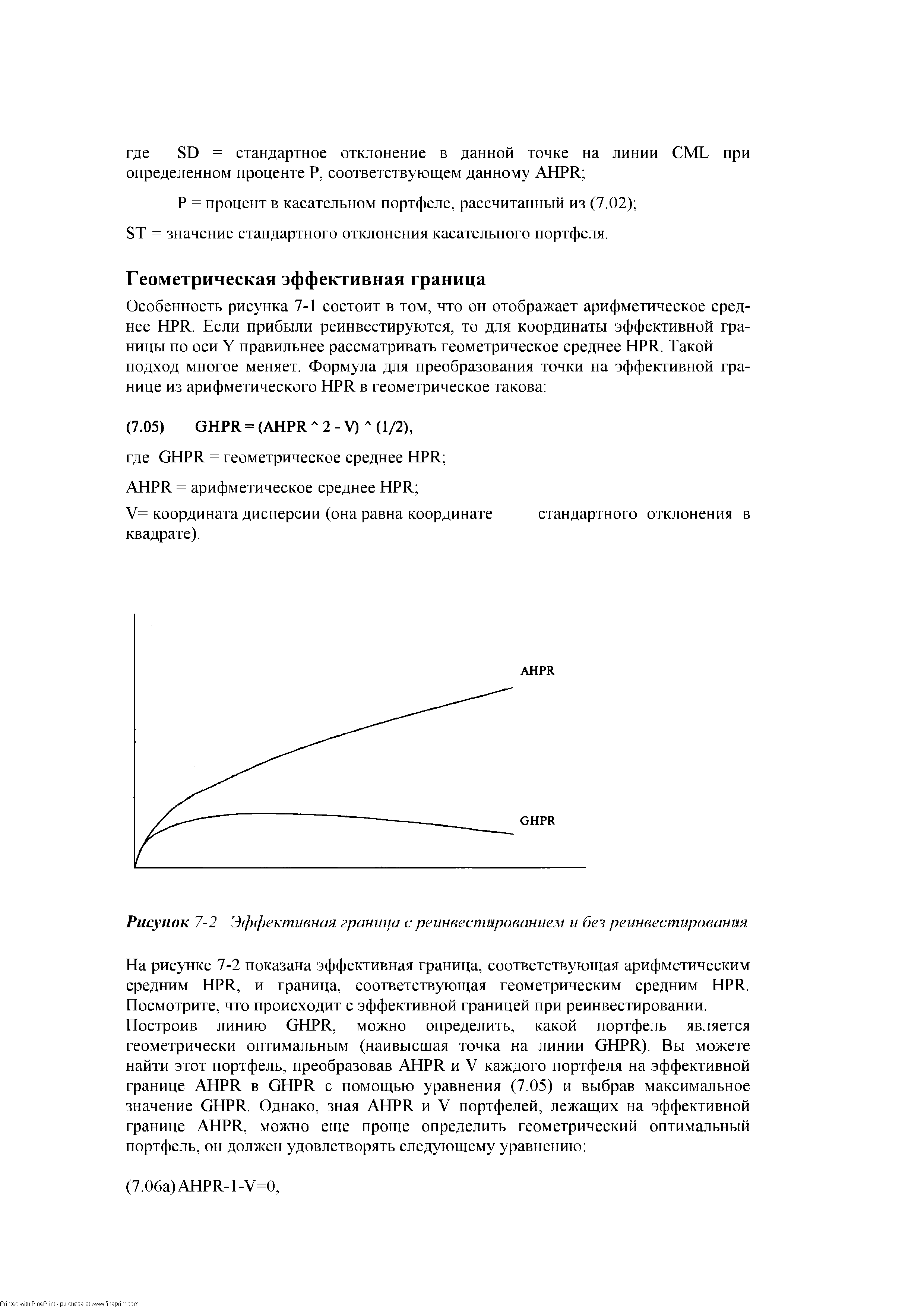 |
Рисунок 7-2 показывает эффективные границы на основе одной сделки. Мы можем преобразовать геометрическое среднее HPR в TWR с помощью уравнения [c.207]
Минутку, — можете возразить вы. — Если мы изменим оптимальный портфель посредством оптимального f, будет ли он оптимальным. Если новые значения относятся к другому портфелю, то ему соответствует другая координата прибыли, и он может не оказаться на эффективной границе . [c.216]
Основные концепции современной теории портфеля изложены в монографии, написанной доктором Гарри Марковицем. Первоначально Маркович предположил, что управление портфелем является проблемой структурного, а не индивидуального выбора акций, что обычно практикуется. Марковиц доказывал, что диверсификация эффективна только тогда, когда корреляция между включенными в портфель рынками имеет отрицательное значение. Если у нас есть портфель, составленный из одного вида акций, то наилучшая диверсификация достигается в том случае, если мы выберем другой вид акций, которые имеют минимально возможную корреляцию с ценой первой акции. В результате этого, портфель в целом (если он состоит из этих двух видов акций с отрицательной корреляцией) будет иметь меньшую дисперсию, чем любой вид акций, взятый отдельно. Марковиц предположил, что инвесторы действуют рациональным способои и при наличии выбора предпочитают портфель с меньшим риском при равном уровне прибыльности или выбирают портфель с большей прибылью, при одинаковом риске. Далее Марковиц утверждает, что для данного уровня риска есть оптимальный портфель с наивысшей доходностью, и таким же образом для данного уровня доходности есть оптимальный портфель с наименьшим риском. Портфель, доходность которого может быть увеличена без сопутствующего увеличения риска или портфель, риск которого можно уменьшить без сопутствующего уменьшения доходности, согласно Марковичу, неэффективны. Рисунок 1-7 показывает все имеющиеся портфели, рассматриваемые в данном примере. Если у вас портфель С, то лучше заменить его на портфель А, где прибыль такая же, но с меньшим риском, или на портфель В, где вы получите большую прибыль при том же риске. Описывая эту ситуацию, Марковиц ввел понятие эффективная граница (effi ient frontier). Это набор портфелей, которые находятся в верхней левой части графика, то есть портфели, прибыль которых больше не может быть увеличена без увеличения риска, и риск которых не может быть уменьшен без уменьшения прибыли. Портфели, находящиеся на эффективной границе, называются эффективными портфелями (см. Рисунок 1-8). Портфели, которые находятся вверху справа и внизу слева, в целом недостаточно диверсифицированы по сравнению с другими портфелями. Те же портфели, которые находятся в середине эффективной границы, обычно очень хорошо диверсифицированы. Выбор портфеля инвестором зависит от степени неприятия риска инвестором — иначе говоря, от желания взять на себя риск. В модели Марковица любой портфель, который находится на эффективной границе, является хорошим выбором, но какой именно портфель выберет инвестор — это вопрос личного предпочтения (позднее мы увидим, что есть точное оптимальное расположение портфеля на эффективной границе для всех инвесторов). Модель Марковица первоначально была представлена для портфеля акций, который инвестор будет держать достаточно долго. Поэтому основными входными данными были ожидаемые доходы по акциям (определяется как ожидаемый прирост цены акции плюс дивиденды), ожидаемые дисперсии этих доходов и корреляции доходов между различными акциями. Если бы мы [c.41]
В какой именно точке на эффективной границе вы будете находиться (то есть какова эффективная КСП), является функцией вашего собственного неприятия риска, по крайней мере, в соответствии с моделью Марковица. Однако есть оптимальная точка на эффективной границе, и с помощью математических методов можно найти эту точку. Если вы выберете КСП с наивысшим средним геометрическим HPR, то достигнете оптимальной КСП Мы можем рассчитать среднее геометрическое из среднего арифметического HPR и стандартного отклонения HPR (обе эти величины у нас уже есть, так как они являются осями X и Y модели Марковица ) Уравнения (1.16а) и (1.166) дают нам формулу для оценочного среднего геометрического EGM (estimated geometri mean). Данный расчет очень близок (обычно до четвертого или пятого знака после запятой) к реальному среднему геометрическому, поэтому можно использовать оценочное среднее геометрическое вместо реального среднего геометрического. [c.45]
AHPR будет важно позднее, при поиске эффективной границы совокупности нескольких рыночных систем, когда необходимо будет определить ожидаемую прибыль (арифметическую) данной рыночной системы. Эта ожидаемая прибыль равна AHPR-1. Рассмотренный метод не обязательно должен быть основан на параметрическом подходе. Возможен и эмпирический подход. Другими словами, мы можем взять отчет о сделках данной рыночной системы и использовать [c.147]
Из предыдущей главы мы узнали, как параметрически вывести эффективную границу. Мы можем улучшить любой портфель путем инвестирования определенной его доли в наличные (или, что то же самое, в беспроцентный вклад). Рисунок 7-1 демонстрирует эту ситуацию графически. [c.201]
Точка В соответствует касательному портфелю. Это единственный портфель, лежащий на эффективной границе, которого коснется линия, проведенная из точки с координатой безрисковая ставка прибыли на вертикальной оси и ноль на горизонтальной оси. Любая точка на отрезке АВ соответствует портфелю из точки В в комбинации с безрисковыми активами. В точке В все средства вложены только в портфель, а в точке А только в безрисковые активы. Любая точка между А и В соответствует определенной комбинации, когда часть активов находится в портфеле, а часть в безрисковых активах. Отметьте, что портфель на отрезке АВ более выгоден, чем любой портфель на эффективной границе при том же уровне риска, так как, находясь на отрезке АВ, он имеет более высокую прибыль при том же уровне риска. Таким образом, инвестору, который хочет получить менее рискованный портфель, чем портфель В, следует инвестировать средства в портфель В и в безрисковьте активы, а не смещаться по эффективной границе в точку с меньшим риском. Линия, выходящая из точки А безрискового уровня на вертикальной оси и нуля на горизонтальной оси и касающаяся в одной точке эффективной границы, называется линией рынка капитала ( ML). Справа от точки В линия ML представляет портфели, где инвестор занимает средства для инвестирования в портфель В. Отметьте, что инвестору, который хочет получить большую прибыль, чем дает портфель В, следует поступить именно таким образом, поскольку портфели на линии ML справа от точки В дают более высокую прибыль, чем портфели на эффективной границе при том же уровне риска. Как правило, В — очень хорошо диверсифицированный портфель. Большинство портфелей, расположенных справа сверху и слева снизу на эффективной границе, имеют очень мало компонентов, портфели в середине эффективной границы, где проходит касательная, достаточно хорошо диверсифицированы. Традиционно считается, что все разумные инвесторы хотят получить максимальную прибыль при данном риске и принять наименьший риск при заданной прибыли. Таким образом, все инвесторы хотят быть где-то на линии ML. Другими словами, все инвесторы хотят держать один и тот же портфель, но с различной долей заемных средств. Данное различие между инвестиционным решением и инвестированием с использованием заемных средств известно как теорема разделения. Мы будем исходить из того, что вертикальная шкала (Е в теории Е — V) выражает арифметическое среднее HPR (AHPR) для портфелей, а горизонтальная шкала (V) отражает стандартное отклонение HPR. Для заданной безрисковой ставки мы можем определить, где находится [c.202]
Следующая таблица показывает, как использовать уравнение (7.Ola). В первых двух столбцах указаны координаты различных портфелей на эффективной границе. Координаты даны в формате (AHPR, SD), что соответствует осям Y и X рисунка 7-1. В третьем столбце представлены данные, полученные из уравнения (7.Ola), при безрисковой ставке 1,5% (AHPR= 1,015). Мы исходим из того, что HPR имеют квартальные значения, таким образом, квартальная безрисковая ставка 1,5% примерно равна годовой безрисковой ставке 6%. Например, для третьего набора координат (1,002 0,00013) получим [c.203]
GHPROPT = среднее геометрическое HPR геометрического оптимального портфеля, т.е. координата Е портфеля на эффективной границе. [c.210]
При решении уравнений с (7. Оба) по (7.06г) необходимо использовать метод итераций, т.е. выбирать тестируемое значение для Е и решать матрицу для этого Е. Если полученное значение дисперсии больше значения Е, это означает, что тестируемое значение Е слишком высокое и в следующей попытке следует его понизить. Вы можете определить дисперсию портфеля, используя одно из уравнений с (6. Оба) по (б.Обг). Повторяйте процесс, пока не будет выполняться любое из равенств с (7. Оба) по (7.06г). Таким образом вы получите геометрический оптимальный портфель (отметьте, что все рассмотренные портфели на эффективной границе AHPR или на эффективной границе GHPR определяются с учетом того, что сумма весов равна 100%, или 1,00). Вспомните уравнение (6.10), используемое в первоначальной расширенной матрице для поиска оптимальных весов портфеля, уравнение отражает тот факт, что сумма весов равна 1 [c.210]
Отметим важный факт структура неограниченного портфеля (для которого сумма весов больше 1, a NI является частью портфеля) неизменна для любого уровня Е единственным отличием является величина заемных средств (величина рычага). Для портфелей, лежащих на эффективной границе, когда сумма весов ограничена, это не так. Другими словами, для любой точки на неограниченных эффективных границах (AHPR или GHPR) отношения весов различных рыночных систем всегда одинаковы. [c.217]
Таким образом, мы можем утверждать, что эффективные границы портфелей с неограниченной суммой весов содержат одинаковые портфели с разным уровнем заемных средств (с разным плечом). Портфель, в котором меняется величина плеча для получения заданного уровня прибыли Е, когда снято ограничение суммы весов, будет иметь второй множитель Лагранжа, равный нулю, при сумме весов, равной 1. Теперь мы можем достаточно просто определить, каким будет наш неограниченный геометрический оптимальный портфель. Сначала найдем портфель, который имеет нулевое значение для второго множителя Лагранжа, когда сумма весов ограничена 1,00. Одним из способов поиска такого портфеля является процесс итераций. Получившийся в результате портфель поднимается (или опускается) рычагом в зависимости от выбранного Е для неограниченного портфеля. Значение Е, удовлетворяющее любому уравнению с (7.Оба) по (7.06г), и будет тем значением, которое соответствует неограниченному геометрическому оптимальному портфелю. Для выбора геометрического оптимального портфеля на эффективной границе AHPR для портфелей с неограниченными весами, можно использовать первый множитель Лагранжа, который определяет положение портфеля на эффективной границе. Вспомните (см. главу 6), что одним из побочных продуктов при определении состава портфеля методом элементарных построчных преобразований является первый множитель Лагранжа. Он выражает мгновенную скорость изменения дисперсии по отношению к ожидаемой прибыли (с обратным знаком). Первый множитель Лагранжа, равный - 2, означает, что в этой точке дисперсия изменяется по отношению к ожидаемой прибыли со скоростью 2. В результате, мы получим портфель, который геометрически оптимален. (7.06д) L1 = - 2, [c.218]
