Лагранжа теорема, 179 Лагранжа функция, 179, 189 [c.490]
Q = S Gj(Fj). Для этого воспользуемся теоремой Куна-Таккера. Вводится вспомогательная функция Лагранжа [5] [c.23]
Так, использование теоремы Лагранжа о среднем значении в условиях, [c.5]
ТЕОРЕМА ЛАГРАНЖА О КОНЕЧНЫХ [c.45]
ТЕОРЕМА ЛАГРАНЖА И СВЯЗАННЫЕ С НЕЙ [c.45]
Геометрическая интерпретация теоремы Лагранжа приведена на рис. [c.48]
Из теоремы Лагранжа следует, что на кривой у = /00 между точками [c.48]
Дифференциальная теорема Лагранжа о среднем значении, записанная [c.48]
| Рис. 2.3. Графическая интерпретация теоремы Лагранжа |  |
| Рис. 2.4. Иллюстрация применения теоремы Лагранжа для определения | 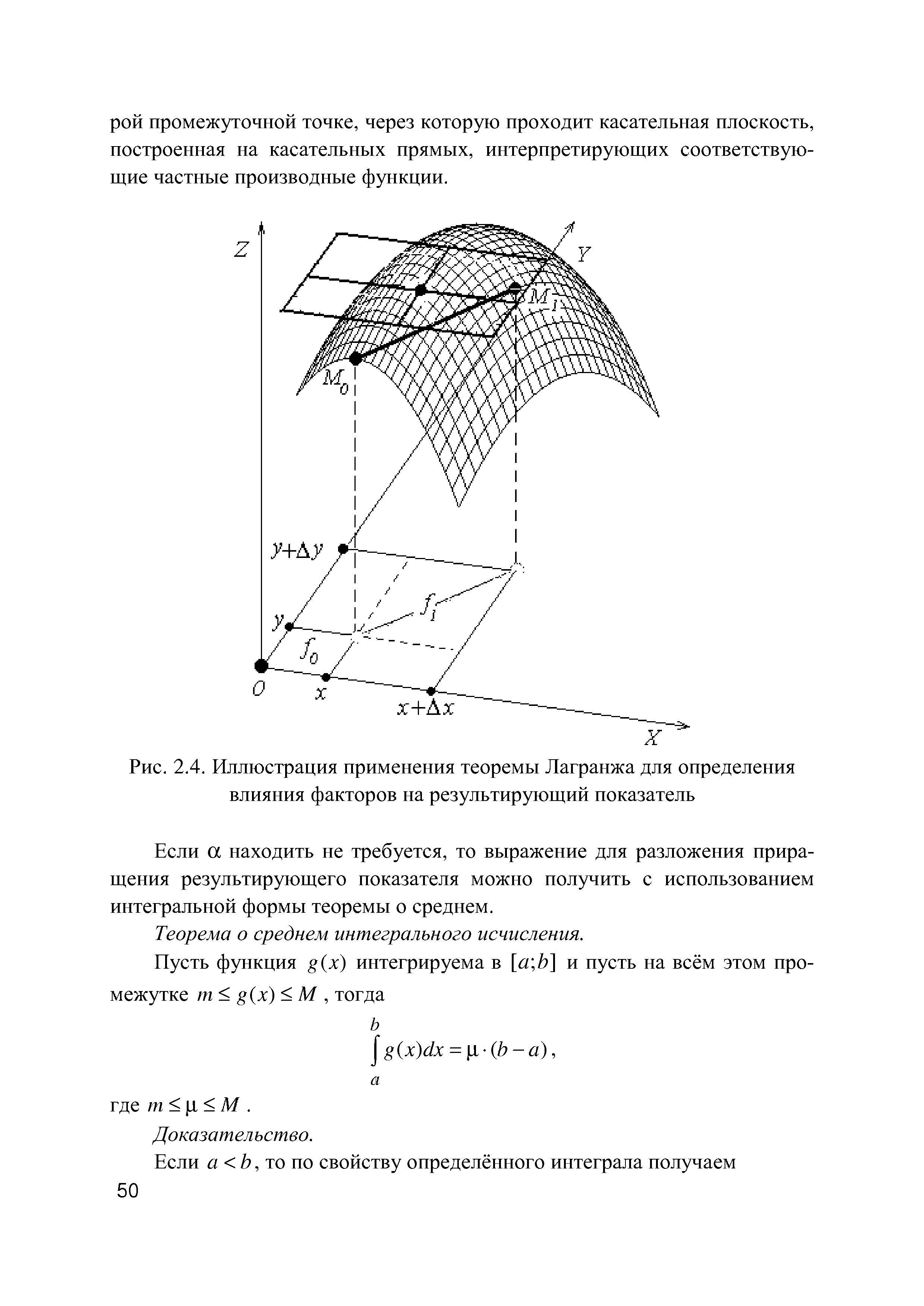 |
Применяя метод Лагранжа, основанный на теореме о промежуточном [c.88]
ПРИМЕНЕНИЕ ТЕОРЕМЫ ЛАГРАНЖА [c.94]
Применение теоремы Лагранжа для разложения приращения показа- [c.102]
Основные теоремы Э.б. утверждают, что при определенных условиях конкурентное равновесие оптимально по Парето и любое оптимальное по Паре-то распределение ресурсов может быть достигнуто в конкурентной экономике. Впрочем, некоторые теоретики полагают, что оптимум в принципе может быть достигнут и без конкуренции, напр. в плановой экономике, если устанавливаемые "сверху" цены соответствуют оптимальным оценкам (множителям Лагранжа), полученным при решении задачи максимизации благосостояния при ресурсных ограничениях. Однако в реальной практике эта гипотеза пока не получила подтверждения, да и вряд ли получит жизнь всегда сложнее любой самой изощренной математической схемы. [c.401]
Утверждения 9.1 и 9.2 следуют из доказанной теоремы. Действительно, в задаче (9.25) усреднение производится по всем переменным, размерность функции / равна т, и функция L, фигурирующая в (9.37) и (9.44), совпадает с функцией Лагранжа R задачи (9.23). [c.323]
Достигает ли функция Лагранжа максимума в точке ж Условие (9.79) теоремы Куна-Таккера совпадает по форме с необходимым условием максимума функции Лагранжа R на множестве Vx. В связи с этим возникает желание заменить условие (9.79) условием [c.335]
Из теоремы Куна-Таккера для задачи НП вытекает, таким образом, что найдется вектор А-множителей Лагранжа, для которого функция R достигает абсолютного максимума по переменным xv E Vx и 7 Е V-y на элементе множества D допустимых решений задачи НП. Отсюда следует, что расширение Лагранжа для задачи НП эквивалентно. Как для любого эквивалентного параметрического расширения А-множители удовлетворяют условию [c.371]
Доказательство. Пусть и ф 0 — вектор из Rn, такой что с + и В (с). Тогда по теореме о среднем значении действительной функции (об остаточном члене в форме Лагранжа) [c.166]
Теорема Лагранжа устанавливает метод (известный как метод множителей Лагранжа ) нахождения необходимых условий экстремума при наличии ограничений типа равенств. Определим сначала функцию Лагранжа ф [c.179]
Замечание. Для доказательства (строгой) выпуклости (вогнутости) функции Лагранжа ф можно воспользоваться определением из 4.9, теоремами 5 или 6, а также (если ф дважды дифференцируема) теоремой 7. Заметим, кроме того, что [c.190]
Безусловно, эта задача математически эквивалентна случаю, когда X и G — векторы, а не матрицы, так что все теоремы остаются справедливыми. Введем тр множителей А (по одному на каждое ограничение gij(X) = 0, г = 1,. . . , m j = 1,.. . , р), и определим т х р матрицу множителей Лагранжа L = ( ij). Тогда функция Лагранжа имеет удобный вид [c.190]
Третье доказательство теоремы 1. Рассмотрим функцию Лагранжа [c.395]
Теорема Лагранжа. Если функция непрерывна на отрезке [а, 6] и дифференцируема в интервале (а, 6), то существует такая точка с Е (а, Ь], что [c.128]
П Пусть а и b — различные корни дифференцируемой функции, т.е. /(а) = 0, /(6) = 0. Из теоремы Лагранжа получаем [c.130]
П Необходимое условие постоянства функции (если функция постоянна на некотором промежутке, то ее производная равна нулю) следует из формулы с = 0. Достаточное условие постоянства функции (если производная равна нулю в каждой точке некоторого промежутка, то функция есть тождественная постоянная на этом промежутке) есть следствие 1 из теоремы Лагранжа, которое уже было ранее доказано (см. с. 129). [c.140]
П Пусть xi и ж 2 принадлежат промежутку, в котором f (x) > > 0 будем считать, что х < х%. По теореме Лагранжа [c.140]
Теорема Лагранжа (теорема о среднем дифференциального исчисле- [c.47]
Блюмин С.Л. Применение теоремы Лагранжа в экономическом факторном [c.141]
Блюмин С.Л. Теорема Лагранжа для эластичностей в индексном экономиче- [c.141]
| Рис. 8.1. Иллюстрации к теоремам Лагранжа и Ролля |  |
