Определение. Асимптотой графика функции у = /(ж) называется прямая, обладающая тем свойством, что расстояние от точки (ж, /(ж)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. [c.166]
Вертикальные асимптоты. График функции у — /(ж) при х —> а имеет вертикальную асимптоту, если [c.166]
Горизонтальные асимптоты. График функции у = f(x) при х —ь +оо или х —> — оо имеет горизонтальную асимптоту, если существует и конечен хотя бы один из пределов [c.167]
Наклонные асимптоты. Наклонной асимптотой графика функции у = f(x) называется ее асимптота, задаваемая уравнением [c.168]
Асимптоты графика функции 171 [c.171]
Задача. Найти асимптоты графиков функций у = ж2, у = [c.173]
Ответ График функции у = ж2 не имеет асимптот. Графики функций у = ж2/(1 + ж2) и у = ж/(1 + ж2) имеют двусторонние горизонтальные асимптоты, которые изображены на рис. 9.21. (Асимптотой графика функции у = ж /(1 + ж ) является прямая у = 1, а асимптотой графика функции у = ж/(1 + ж2) является ось абсцисс.) [c.173]
Асимптоты. Асимптотой графика функции называется прямая, к которой сколь угодно близко приближается график данной функции при стремлении аргумента к бесконечности или к некоторому числу а или случай вертикальной асимптоты. Асимптоты могут быть вертикальными, горизонтальными и наклонными. [c.25]
Определение. Прямая, имеющая уравнение у = kx + Ь, называется наклонной асимптотой графика функции у=/(х) при х-> оо, [c.68]
Имеет место и обратное из последних соотношений следует, что прямая у kx + b является наклонной асимптотой графика функции y — f(x). По выведенным формулам вычисляются угловой коэффициент k и начальная ордината b двух асимптот у = kx + b отдельно при х - + > и при х - -оо. Очевидно, что если k == 0, то уравнение асимптоты примет вид у = Ь. [c.68]
Асимптоты графика функции 118 6.3.5 Схема исследования графика функции 119 [c.5]
Асимптоты графика функции jn, твоим переменной [c.105]
Асимптота графика функции 109 Ацикличный набор 210 [c.327]
Соответствие у=/[х) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины х аргумента или независимой переменной) соответствует определенное значение другой величины, у (зависимой переменной или Ф. в значении 1). Ф. задана, если известен закон, определяющий такое соответствие. На практике она задается формулой, таблицей или графиком (есть и другие способы, напр. алгоритмический — см. Алгоритм). При построении графика функции анализируются такие ее свойства, как четность или нечетность, нулевые значения, периодичность (см. Периодическая функция), монотонность (см. Монотонная функция), наличие асимптоты и др. [c.379]
График функции может иметь также и наклонную асимптоту. Таков, например, график функции у = х + 1/х. При удалении точки графика от начала координат расстояние до прямой у — х неуклонно сокращается (рис. 9.17, в). [c.165]
В случае, когда конечные пределы 6Л и 6П совпадают 6Л = 6П, говорят, что график функции у = /(ж) имеет двустороннюю горизонтальную асимптоту у = Ь. Примеры двусторонних горизонтальных асимптот приведены на рис. 9.21. [c.167]
| Рис. 9.22. Графики функций и их асимптоты | 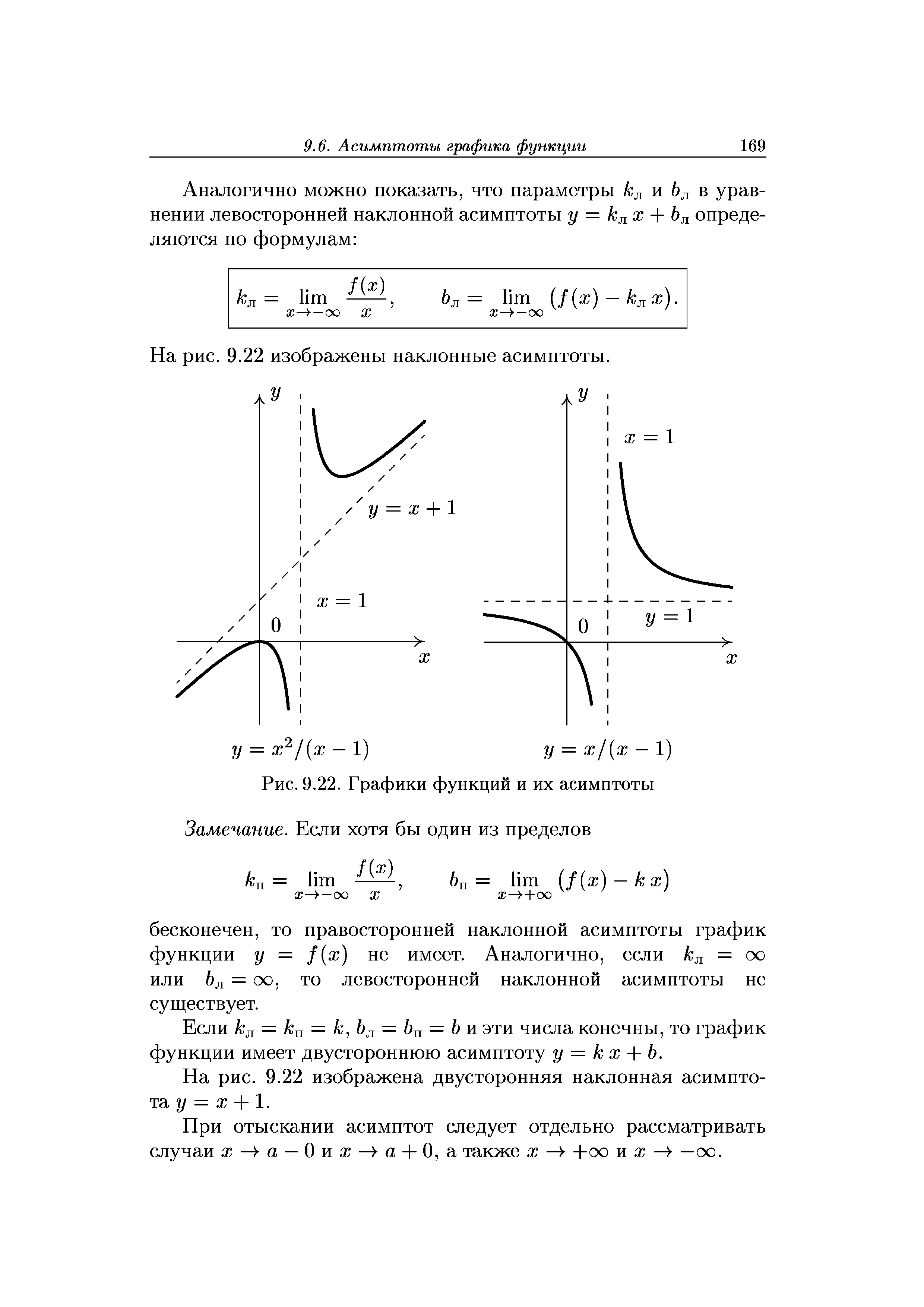 |
Вертикальных асимптот график этой функции не имеет, так как функция у = ж3 — 3 х не имеет разрывов. [c.173]
Таким образом, л = п = оо. Следовательно, график функции не имеет также наклонных асимптот и горизонтальных асимптот (если бы горизонтальная асимптота существовала имели бы k = 0). [c.173]
Итак, график функции не имеет асимптот ни вертикальных, ни наклонных, ни горизонтальных. А [c.173]
Этот тип кривых (рис. 6.3) характеризуется двумя асимптотами (прямыми, к которым график функции неограниченно приближается, не достигая их) горизонтальной у = а и вертикальной х = 0, а также параметром искривления Ь. С помощью преобразования независимой переменной х = l/х (т. е. перехода к новому аргументу) эта зависимость приводится к линейному виду у = а + Ьх [c.185]
Областью определения и областью существования функций являются интервалы (-оо, 0) и (0, +оо). Функции нечетные. Графики их расположены в первой и третьей четвертях, оси координат также служат асимптотами, на всей области определения функции убывающие. Графики функций называют гиперболами (см. рис.2.86). [c.30]
Итак, прямая, имеющая уравнение у = х + 2, является наклонной асимптотой графика данной функции при х - оо. Таким образом, фафик данной функции имеет вертикальную асимптоту, имеющую уравнение х = 2, и наклонную асимптоту, имеющую уравнение у = х + 2 (см. рис. 4.9). [c.69]
Нахождение минимального и максимального значения функции на интервале. Нахождение минимального и максимального значения выпуклой функции на интервале. Схема построения и исследования графика функции с использованием производной. Вертикальные и наклонные асимптоты функции. [c.14]
Исследовав стандартным методом функцию fl3)(f), найдем, что она определена на (0, +°°), не является ни четной, ни нечетной и ни периодической, возрастает на промежутке (0, 2/3) и убывает на промежутке (2/3, -н ) точка 2=2/3 является точкой максимума, а сам максимум равен тах/(3)(0 =0,784 точки ,=(2-V2)/3 и t, = (2+V2)/3 являются точками перегиба графика этой функции, ] /(3)(0=1 Хз)(0=0, т.е. ось Ot является для графика функции 7<з>(0 горизонтальной асимптотой. На основании полученных данных построим график функции fl3)(f), который имеет следующий вид (см. рис. 7.5). [c.118]
Так как функция является непрерывной, то ее график не имеет вертикальных асимптот. Наклонных и горизонтальных [c.175]
Функции характеризуются рядом свойств, к важнейшим из которых (для построения и исследования графиков) относятся четность, нули, периодичность, монотонность, ограниченность функции, наличие у функций асимптот и обратной функции. Рассмотрим вкратце эти свойства функций. [c.24]
Термин асимптота введен древнегреческим ученым Аполлонием Пергским при изучении гиперболы и происходит от греческого слова асимтотос , означающего несовпадающий . Пусть это слово не вводит вас в заблуждение. Асимптоты гиперболы действительно не пересекают график функции (т. е. являются в некотором смысле несовпадающими ). Однако, согласно современным представлениям об асимптоте, кривая может пересекать свою асимптоту (например, график затухающих колебаний, изображенный на рис. 9.18). [c.165]
Итак, А п = А л = А = 1и6п = 6л = 6=1, следовательно, график функции имеет наклонную асимптоту у = ж + 1. [c.172]
Смотреть страницы где упоминается термин Асимптота графика функции
: [c.169] [c.170] [c.68] [c.118] [c.167] [c.105] [c.47] [c.28] [c.29] [c.31]Справочник по математике для экономистов (1987) -- [ c.105 ]
