Для прогнозирования народнохозяйственной потребности (потребность внутреннего рынка страны) используется динамическая модель, представляющая собой систему дифференциальных уравнений или уравнений в конечных разностях. Коэффициентом уравнений служит скорость изменения потребности, зависящая от времени и факторов, влияющих на изменение потребности. Решение дифференциальных уравнений дает возможность найти зависимость потребности в средствах производства от скорости ее изменения. Таким образом, в такой постановке проблемы задача прогнозирования потребности в средствах производства сводится к задаче прогнозирования скорости ее изменения или темпов прироста (снижения) потребности. [c.136]
Решение дифференциального уравнения (6) представляет со- [c.79]
При численном решении дифференциальных уравнений их часто заменяют разностными. Это возможно, если решение Р.у. стремится к решению соответствующего дифференциального уравнения, когда интервал Д стремится к нулю. [c.299]
Несмотря на то, что аналитические решения дифференциального уравнения, описывающего перенос и турбулентную диффузию примеси, могут быть получены при определенной стилизации атмосферных процессов, возможности их использования значительно расширяются, если взаимно однозначно связать распределение примесей с вероятностными интегральными и дифференциальными функциями распределения метеорологических параметров. Причем идея метода при различных модификациях справедлива для описания распределения примесей как легких, так и тяжелых, обладающих собственной скоростью осаждения. Этот метод особенно экономичен при расчете распределения легкой пассивной консервативной примеси. [c.120]
Методика оценки возраста осадка по измерениям современных уровней радиоактивности изотопов урановой серии. Общее решение дифференциальных уравнений радиоактивного распада для изотопов урановой серии имеет вид [c.134]
При исследовании задач оптимального управления, ввиду, как правило, разрывности управляющих воздействий, возникает необходимость рассматривать решения дифференциальных уравнений, определяющих допустимый процесс, в неклассическом или в обобщенном виде. Особенно остро эта проблема стоит для систем уравнений с частными производными, где зачастую невозможно построение не только гладкого, но и просто непрерывного решения, соответствующего допустимому управлению. [c.335]
Выразим из решения дифференциальных уравнений (4.52) и (4.53) температуры источников в конце полуциклов через их продолжительности [c.153]
Состояние равновесия Это решения дифференциального уравнения [c.153]
Поскольку первообразной от постоянной величины 3 , является линейная функция 3 k t + С, то решение дифференциального уравнения представляет функцию y(i] — 3 k t + С. Воспользовавшись другим условием задачи, согласно которому [c.358]
Функция ф(х), х G (а, 6), называется решением дифференциального уравнения (17.3), если она имеет производную ф (х] на (а, 6), и если для любого ж (а, 6) справедливо равенство [c.359]
Другими словами, функция ф(х], х (а, 6), называется решением дифференциального уравнения (17.3), если уравнение (17.3) при подстановке ее вместо у обращается в тождество по х на интервале (а, 6). [c.360]
Аналогично определяется решение дифференциального уравнения (17.2). [c.360]
V Пример. Найти решение дифференциального уравнения [c.362]
Общим решением дифференциального уравнения второго порядка (18.3) называется функция [c.370]
В зависимости от способов решения дифференциальные уравнения второго порядка разделяются на различные типы. Простейшим типом является уравнение [c.370]
Задача 2. Найти частное решение дифференциального уравнения четвертого порядка [c.401]
Принципиальное отличие этого функционала от функционала (1) уже обсуждалось в 4. Возможность с достаточной точностью аппроксимировать вариацию функционала (1) выражением (7) с небольшим числом k связана с гладкостью функции 8ж (f), являющейся решением дифференциального уравнения в вариациях следствием этого является и гладкость функции Фх [х (t)]bx (t), значения которой в окрестностях точек аппроксимации, грубо говоря, меняются при вариации управления в ту же сторону, в какую они меняются в точках аппроксимации. Поэтому, учитывая 8Ф при построении 8ц ( ) только в точках аппроксимации, мы в известной мере учитываем 8Ф всюду, где Ф [х (г)] тах Ф [х (t)], Для функционала (2) это уже не так, Ьи (f) — измеримая функция, ее значения в близких точках t, t" никак не связаны между собой, и аппроксимация типа (7) — неэффективна. Разумеется, она будет эффективна, если разместить по точке аппроксимации на каждом интервале счетной сетки (tn, tn+l), входящем в множество М. Однако в проводившихся автором расчетах число таких интервалов было 102, что уже приводит к задаче линейного программирования слишком тяжеловесной для того, чтобы решать ее на каждом шаге процесса построения минимизирующей последовательности управлений. Поэтому в расчетах использовался прием превращения компонент управления, явно входящих в функцию Ф [х, и], в фазовые координаты. Именно, полагаем [c.185]
В общем случае K s — решение дифференциального уравнения с постоянными коэффициентами и многими переменными. Такими переменными могут быть значения bis,t и т.п. Скорректируем выражение (2.2.7) коэффициентами (2.2.8) и получим систему уравнений [c.104]
| Рис. 6.3.5. Структурная схема решения дифференциального уравнения (6.3.19) | 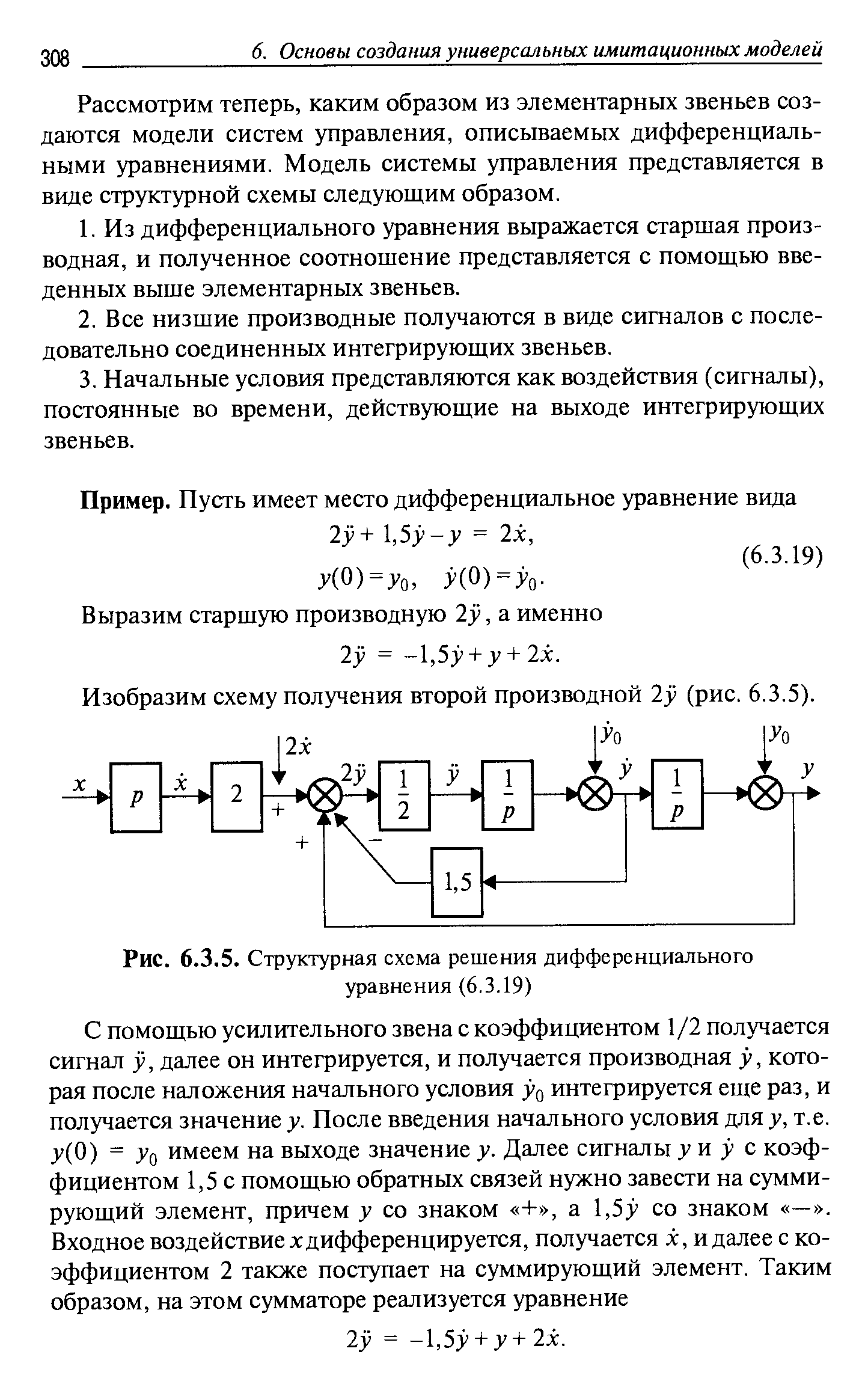 |
Подпрограммы из группы математики предназначены для обращения матриц, решения системы линейных алгебраических уравнений, интегрирования и дифференцирования функций, решения дифференциальных уравнений, нахождения действительных и комплексных корней многочленов, аппроксимации, интерполяции. [c.182]
ИНТЕГРИРОВАНИЕ — процесс решения дифференциального уравнения или действие отыскания неизвестного интеграла. [c.249]
П5.8. Решение дифференциальных уравнений [c.179]
Задачи математической экономики, приводящие к дифференциальным уравнениям. Дифференциальное уравнение. Решение дифференциального уравнения. Общее решение дифференциального уравнения. Задача Коши. Теорема существования и единственности решения задачи Коши. [c.16]
Следовательно, частное решение дифференциального уравнения (3.1) можно записать [c.117]
ИНТЕГРИРОВАНИЕ [integration] — 1. Операция отыскания неопределенного интеграла, решения дифференциального уравнения. [c.126]
Решение дифференциальных уравнений с помощью пакета Maple 401 [c.401]
Обратите внимание на вырожденность временнбй сетки по существу, [О, Т] разбит только на два счетных интервала, остальные — практически нулевые. Этот же дефект имеет решение второго варианта задачи ([77], таблица на стр. 151). Никакого отношения к решению дифференциальных уравнений табличные функции не имеют. Любопытно, что одно из таких решений было проконтролировано расчетом с N=20, получено совпадение по функционалу с точностью до 0,15%, и можно утверждать, что ошибка дискретизации является допустимой для практики ([77], стр. 151). Это совпадение связано, видимо, с тем, что и сетка с N=20 столь же вырождена и состоит из тех же двух счетных интервалов. 2 Содержательное обсуждение подобных решений бессмысленно, здесь нельзя даже говорить о какой-то, пусть не очень высокой, точности. Характерноз что используемый метод полностью обосяо- [c.310]
Вазов В., Форсайт Дж. Разностные методы решения дифференциальных уравнений, с частными производными. — М. ИЛ, 1963. [c.479]
Типовуе блоки, используемые в имитационных моделях, могут отображать фактически любые математические схемы, включая схемы теории игр, конечных автоматов, оптимальных решений, дифференциальных уравнений, теории расписаний и множество других математических приложений. Главное правило при использовании того [c.286]
На аналоговых машинах решают, разумеется, и более сложные задачи. Они, например, нередко используются для решения дифференциальных уравнений. Точность их обычно невелика, значительно меньше, чем достигаемая на ЭЦВМ. [c.145]
Бахвалов Н.С. Оценки близости решений дифференциальных уравнений. — Труды IV симпозиума по основным проблемам вычислительной математики, Пльзень, 1979. [c.433]
Биномиальный метод, называемый также по имени его авторов методом Кокса-Росса-Рубинштейна ( ox-Ross-Rubinstein), был предложен в 1979 году и является более поздним по отношению к методу Блэка-Шоулса (1973). Однако начинать знакомство с подходами к оценке опционов лучше именно с более простого биномиального метода. В определенном смысле он аналогичен численным методам решения дифференциальных уравнений. Первоначально данный подход применялся для расчета стоимостей американских опционов, для которых отсутствует точное аналитическое решение, а впоследствии был распространен на многие более сложные производные инструменты. В настоящее время численные методы наряду с методами статистических испытаний (Монте-Карло) чаще всего используются в моделях обсчета производных инструментов, так как позволяют максимально учесть реальные условия операций с ними. [c.35]
Смотреть страницы где упоминается термин Решение дифференциального уравнения
: [c.246] [c.154] [c.81] [c.79] [c.160] [c.457] [c.38] [c.53] [c.355] [c.465] [c.609] [c.165] [c.171]Справочник по математике для экономистов (1987) -- [ c.162 ]
