Название книги дало золотое сечение , известное в геометрии со времен Евклида. [c.205]
Лука Пачоли был близок к Леонардо да Винчи, а принципы двойной бухгалтерии он позаимствовал у купцов Генуи и Венеции. Интересно, что в то время в арифметике ещё не было даже общепринятых символов + и - для обозначения сложения и вычитания. В одной из своих других работ Лука Пачоли описал знаменитый принцип золотого сечения. [c.662]
Я не буду утомлять читателя длинными пассажами о числах Фибоначчи, лежащих в основе окружающего нас мира, а просто сошлюсь на многочисленные учебники и статьи, посвященные описанию этой числовой последовательности и так называемого золотого сечения. Я лишь еще раз подчеркну важность числовой последовательности Фибоначчи, включающей в себя следующие числа 1,2, 3, 5, 8, 13, 21, 34, 55 — и т. д. Каждое последующее число ряда получается путем сложения двух предыдущих чисел. По мере роста номера числа в последовательности отношение предшествующего числа к последующему приближается к 0,618, а отношение последующего числа к предшествующему стремится к 1,618. Такая особенность присуща только членам данной последовательности. [c.46]
В этой главе мы не собираемся подвергать исчерпывающему анализу такие понятия, как "золотые сечения", "золотые прямоугольники" и "логарифмические спирали", не говоря уже о математических основах теории волн и собственно числовой последовательности Фибоначчи. Тем не менее необходимо упомянуть о том, что на основе "золотого коэффициента" можно построить так называемую "логарифмическую спираль", каковая, как полагают, отчасти объясняет универсальный принцип роста, некий закон - общий для всей нашей вселенной. Считается, что спираль сохраняет постоянную форму, в каком бы виде она ни представала. [c.350]
Деление двух любых стоящих рядом чисел из ряда Фибоначчи приводило в среднем к числу 0.618, которое считалось числом золотого сечения в древнегреческой и древнеегипетской культурах. Именно это число и стало основой для применения в техническом анализе линий Фибоначчи, где 0.618 превратилось в 61,8%. [c.132]
Числа Фибоначчи тесно связаны с золотым сечением в геометрии. Золотое сечение хорошо известно в математике и архитектуре со времен Древней Греции. Если разделить отрезок единичной длины на две части так, чтобы отношение длины отрезка к большей части равнялось отношению большей части к меньшей, то длина этой большей части ф равна [c.183]
Пропорции золотого сечения в анализе графиков описывают соотношения тенденций (5 волн 1,2,3,4,5) и коррекций (3 волны А, В, С). Оказывается, их использование вместо обычных пропорций 1/3, 1/2, 2/3, дает более точный результат. [c.185]
Отметим, что числа 1.618, 0.618 называются золотым сечением , золотой серединой или золотым коэффициентом . Эти числа являются решением задачи о разделении отрезка на части так, чтобы меньшая часть относилась к большей, как большая ко всему отрезку. [c.125]
Методика прогностических расчетов с использованием чисел Фибоначчи строится на том, что численное соотношение движения и отката должно давать коэффициенты "золотого сечения", то есть [c.166]
Чтобы лучше понять, как ФИ Фибоначчи геометрически встраивается в ФИ-спирали и ФИ-эллипсы, начнем с описания золотого сечения линии и прямоугольника и их соответствующих отношений к ФИ. [c.14]
Линия АВ длиной L разделена на два отрезка точкой С. Пусть длины АС и СВ будут равны а и b соответственно. Если С являет ся такой точкой, что частное L-т- а равно частному a -s-b, то С золотое сечение АВ. Отношение L -ь а или а -А b называется золотым отношением. [c.14]
Конечная точка О называется полюсом равноугольной спирали, которая проходит через золотые сечения D, Е, G, J и так далее. [c.16]
ФИ-спираль — самая красивая из математических кривых. Эта спираль на протяжении миллионов лет встречается в естественном мире на каждом шагу. Ряд суммирования Фибоначчи и золотое сечение, представленное в Главе 1 как геометрический эквивалент ряда суммирования Фибоначчи, очень тесно ассоциируются с этой замечательной кривой. Последовательные камеры раковины наутилуса развиваются по ФИ-спирали. По мере роста раковины размер ее камер увеличивается, но их форма остается неизменной. Два сегмента спирали могут быть различны по размеру, но не по форме. Спираль не имеет конечной точки. Рисунок 6.1 показывает рентгенограмму раковины камерного наутилуса ("кораблика"). Камеры раковины наутилуса растут согласно "божественной пропорции", которая и есть ФИ Фибоначчи (отношение 1.618). [c.147]
Не только египетские пирамиды построены в соответствии с совершенными пропорциями золотого сечения, то же самое явление обнаружено и у мексиканских пирамид. Возникает мысль, что как египетские, так и мексиканские пирамиды были возведены приблизительно в одно время людьми общего происхождения. Пример важной роли скрытой пропорции Ф=1.618 представлен на рис. 1-2а и Ь. [c.5]
Золотое сечение отрезка [c.7]
Греческий математик Евклид применил золотое сечение к отрезку прямой (рис. 1-4). Отрезок АВ длины L делится точкой С на две части. Пусть длины отрезков АС и СВ будут равны соответственно а и Ь. Если точка С такова, что L a равняется а Ь, то С - золотое сечение отрезка АВ. Отношение L a или а Ь называется "золотым отношением". Другими словами, точка С делит отрезок АВ на две части таким образом, что отношения этих частей равны 1.618 и 0.618. [c.7]
| Рис. 1-4 Золотое сечение отрезка. |  |
| Рис. 1-5 Золотое сечение прямоугольника. |  |
ЦИРКУЛЬ ЗОЛОТОГО СЕЧЕНИЯ [c.117]
Рис. А-1 Циркуль золотого сечения. [c.118]
Последовательность Фибоначчи содержит и другие любопытные соотношения, или коэффициенты, но те, которые мы только что привели - самые важные и известные. Как мы уже подчеркнули выше, на самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его "золотым коэффициентом" или "золотым сечением". Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип "золотого сечения" при строительстве Парфенона, египтяне - Великой пирамиды в Гизе. Свойства "золотого коэффициента" были хорошо известны Пифагору, Платону и Леонардо-да-Винчи. [c.349]
Он основан на пропорциях золотого сечения. А само золотое сечение очень тесно связано в математике с числами Фибоначчи. Поэтому-то никто и не удивляется, что подход получил название метода проекций и откатов Фибоначчи. www.fx iub.org [c.180]
Странные цифры. Красивые цифры. Эти соотношения указывают на тесную связь, существующую между золотым сечением и числами Фибоначчи. Пусть это и странное, и неожиданное для нематиматиков свойство, но зато как интригует .. www.fx iub.org [c.184]
Пропорции золотого сечения дают ориентиры не только возможных уровней отката, но и указывают возможную величину хода в случае продолжения тенденции (proje tion). Бывает, что после хода некоторого размаха Н рынок откатывается, а затем продолжает ход в том же направлении. В типичном случае после этого величина продолженного хода может составить 1,618 х Н. [c.187]
Чтобы наложить на график дуги Фиболаччи, отыскивается значимый по величине проход рынка (например, падение от 117 до 108,50 на рис. 6.6). Соответствующие экстремумы соединяются отрезком, который затем делится в пропорциях золотого сечения. Через точки деления отрезка затем проводятся окружности с центром во втором экстремуме. [c.187]
На самом деле Фибоначчи вообще-то не является первооткрывателем этих пропорций. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам. Они называли его "золотым коэффициентом" или "золотым сечением". Его глубокие следы можно обнаружить в музыке, изобразительном искусстве, архитектуре и биологии. Так, греки использовали принцип "золотого сечения" при строительстве Парфенона, египтяне - Великой пирамиды в Гизе. К тому же, свойства "золотого коэффициента" были хорошо известны Пифагору, Платону и Леонардо да Винчи. В общем, многие уважаемые господа знали об этих магических цифрах. Но возникает вопрос а не могут ли они пригодиться и нам И если да, то как же пользоваться таким великим открытием [c.163]
Это отношение стало обрастать разными особыми именами еще даже до того, как другой средневековый математик Лука Па-чиоли (1445—1514) назвал его "божественной пропорцией". Среди его современных названий — "золотое сечение" и " золотая середина". Немецкий астроном Иоганн Кеплер (1571 — 1630) назвал отношение Фибоначчи одним из сокровищ геометрии. В алгебре оно, как правило, обозначается греческой буквой ФИ (ср), а именно [c.10]
Греческий математик Евклид Мегарский (450—370 гг. до н. э.) — первый ученый, написавший о золотом сечении и, таким образом, сосредоточившийся на анализе прямой линии (рисунок 1.3). [c.14]
| Рисунок 1.3 Золотое сечение линии. Источник FAM Resear h, 2000. | 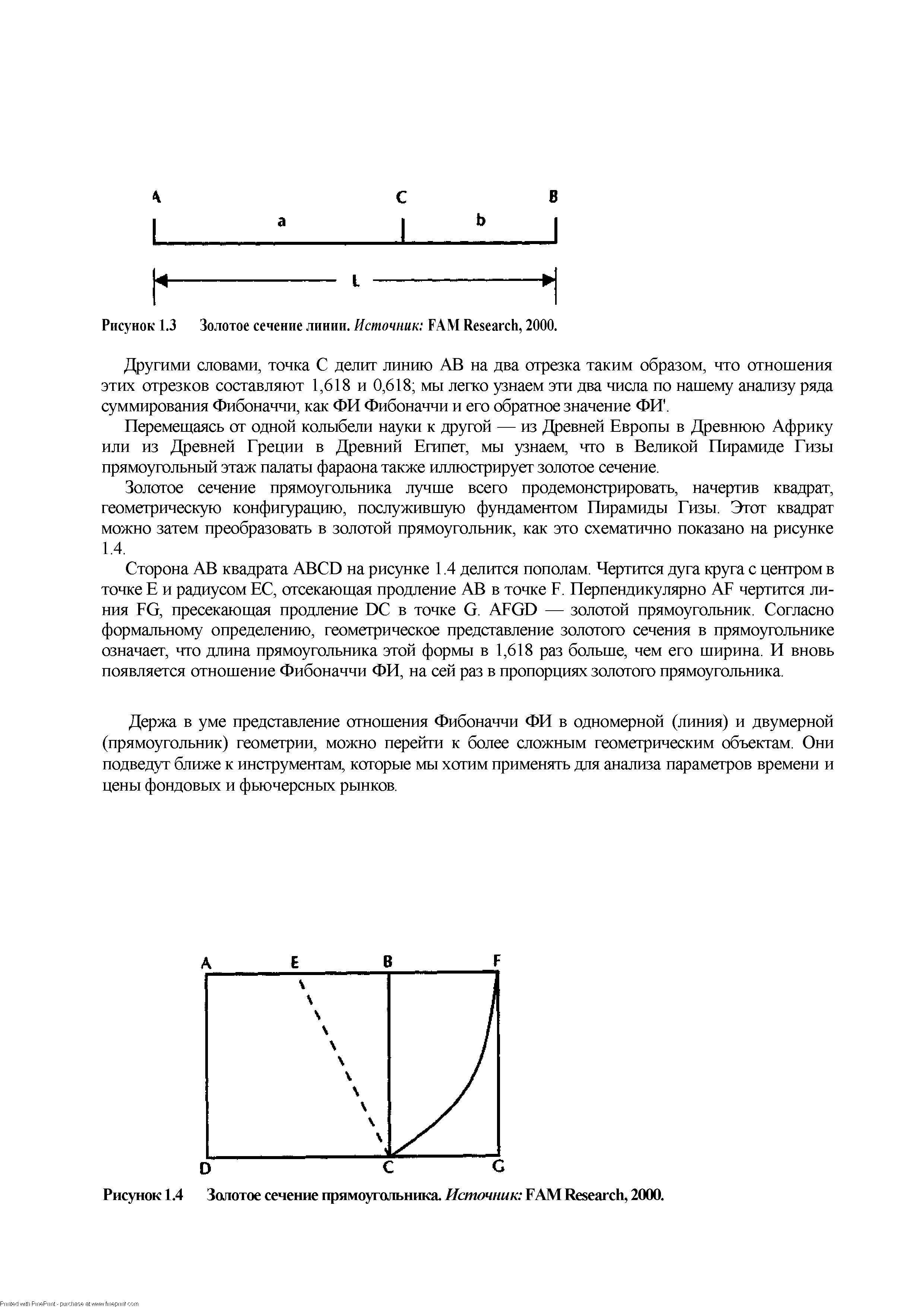 |
Золотое сечение прямоугольника лучше всего продемонстрировать, начертив квадрат, геометрическую конфигурацию, послужившую фундаментом Пирамиды Гизы. Этот квадрат можно затем преобразовать в золотой прямоугольник, как это схематично показано на рисунке 1.4. [c.15]
Сторона АВ квадрата AB D на рисунке 1.4 делится пополам. Чертится дуга круга с центром в точке Е и радиусом ЕС, отсекающая продление АВ в точке F. Перпендикулярно AF чертится линия FG, пресекающая продление D в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сей раз в пропорциях золотого прямоугольника. [c.15]
Единственной математической кривой следующей модели естественного роста является спираль, выраженная в таких природных феноменах, как Spira mirabilis или раковина наутилуса. ФИ-спираль называют самой красивой математической кривой. Этот тип спирали часто встречается в природе. Ряд суммирования Фибоначчи и золотое сечение, представленное выше как его геометрический эквивалент, очень хорошо ассоциируются с этой замечательной кривой. [c.16]
Наш анализ времени основан на открытиях Евклида Мегар-ского и изобретенном им золотого сечения. Об этом уже говорилось ранее в представлении отношения Фибоначчи в геометрии и золотого сечения линии. [c.27]
Читатели в принципе познакомились с анализом временных целей Фибоначчи в Главе 1. Чтобы правильно рассчитать дни временных целей Фибоначчи, используем работу греческого математика Евклида Мегарского и изобретенный им "золотой срез" (также называемый золотым сечением), связывающий закон природы с геометрией. [c.197]
Особые названия этому соотношению начали давать еще до того, как Лука Пачиоли (средневековый математик) назвал его Божественной пропорцией. Среди его современных названий есть такие, как Золотое сечение, Золотое среднее и Отношение вертящихся квадратов. Кеплер назвал это соотношение "одним из сокровищ геометрии". В алгебре общепринято его обозначение греческой буквой фи (Ф = 1.618). [c.3]
В Великой пирамиде прямоугольный пол царской усыпальницы иллюстрирует золотое сечение (рис. 1-5). Лучше всего "золотой прямоугольник" показывать, начав с квадрата - основания пирамиды в Гизе. Сторона АВ квадрата AB D на рис. 1-5 делится пополам. Проводится дуга окружности с центром Е и радиусом ЕС, пересекающая продолжение отрезка АВ в точке F. Перпендикулярно отрезку AF проводится отрезок FG до пересечения с продолжением отрезка D в точке G. Получаем AFGD - золотой прямоугольник. Согласно определению, длина прямоугольника золотого сечения в 1.618 раза превышает ширину. Следовательно, соотношение его пропорций - это число Ф [c.7]
Когда выбрана правильная величина фильтра, этот метод должен очень хорошо работать на трендовых рынках. На боковых рынках он должен сильно ограничить "напрасные дергания" (whipsawing). Примеры минимальных величин фильтра для некоторых товаров приведены ниже. Эти значения были получены "вручную" в 1983г. как часть материала к семинару на тему "Золотое сечение". Последняя проверка показала, насколько это возможно, что эти минимальные значения не изменились. Если в соотношениях Фибоначчи есть смысл, эти числа не зависят от времени. [c.79]
Циркуль золотого сечения был представлен на семинарах, проводившихся автором в 1983г. Это необходимый инструмент для каждого инвестора, интересующегося теорией Фибоначчи. Кроме того, он очень легок в использовании. [c.117]
Циркуль золотого сечения - это превращение суммационной последовательности Фибоначчи в инвестиционный инструмент. Как и у циркуля, его "ножки" могут быть сведены уже или разведены шире (рис. А-1). Эти три ножки всегда остаются разведенными в соответствии с соотношением Фибоначчи, таким образом, всегда возможна динамическая адаптация к циклам. Это инструмент для приложения соотношений 0.618 и 1.618 к любому методу анализа чартов из представленных в этой книге, за исключением спирального (выполнять который необходимо на компьютере). Он поможет работать с [c.117]
