Метод экстраполяции тренда

из "Модели и методы теории логистики Издание 2 "

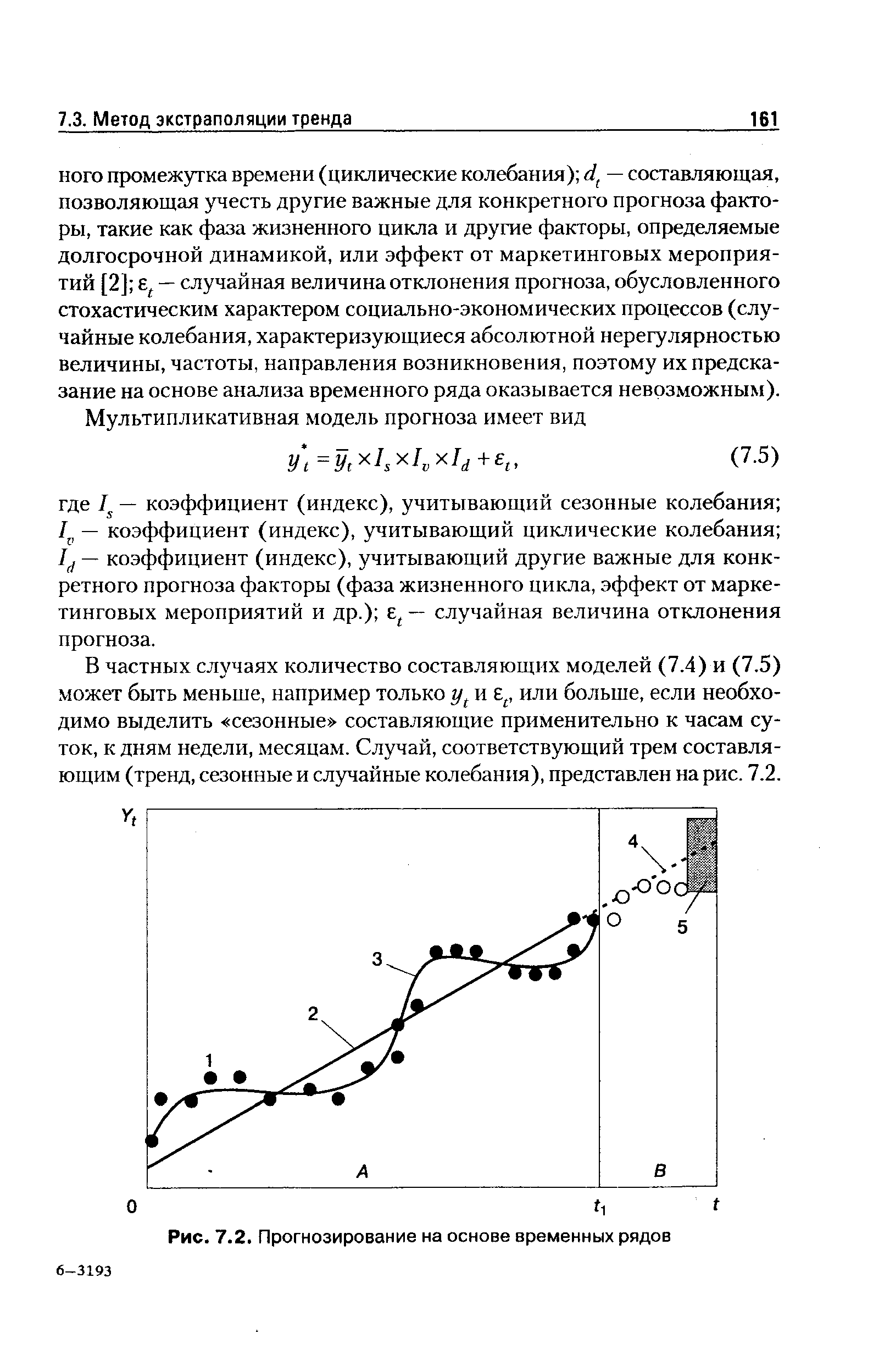
В частных случаях количество составляющих моделей (7.4) и (7.5) может быть меньше, например только yt и е , или больше, если необходимо выделить сезонные составляющие применительно к часам суток, к дням недели, месяцам. Случай, соответствующий трем составляющим (тренд, сезонные и случайные колебания), представлен на рис. 7.2. [c.161]
Рассмотрим простой вариант, когда модели (7.4) или (7.5) содержат только составляющие yt и ег Процедуру прогнозирования в этом случае можно представить в виде следующей последовательности. [c.162]
Первый этап — подбор зависимости для описания уравнения тренда. Видом функции задаются, обычно используются полиномы различных порядков, экспоненциальные, степенные функции и т. п. Параметры модели прогнозирования определяются методом наименьших квадратов (МНК), при этом модель тренда должна быть такой, чтобы сумма квадратов отклонений расчетных значений от фактических была бы наименьшей. [c.162]
Погрешность прогноза отражается в виде доверительного интервала, с помощью которого точечный прогноз преобразуется в интервальный. [c.163]
Как видно из выражения (7.13), К зависит от продолжительности наблюдения (N) и периода упреждения (Z,). [c.164]
Метод наименьших квадратов достаточно прост и легко реализуется на ЭВМ. К недостаткам МНК можно отнести следующее. Во-первых, модель тренда жестко фиксируется и с помощью МНК можно получить достоверный прогноз на небольшой период упреждения. Во-вторых, МНК очень просто реализуется только для линейных зависимостей и нелинейных функций, приводимых к линейному виду. [c.164]
Расчет коэффициентов уравнения а0и а производится по формулам (7.6) и (7.7), которые получены на основе метода наименьших квадратов. [c.165]
Параметр t. определяет для нормального закона число средних квад-ратических отклонений, которые нужно отложить от центра рассеивания (влево и вправо) для того, чтобы вероятность попадания в полученный участок была равна Д. В нашем случае доверительные интервалы откладывают вверх и вниз от среднего значения у(. [c.166]
В табл. 7.9 приведены наиболее часто встречающиеся в практических расчетах значения вероятности /3 и параметра tg для нормального закона распределения. [c.166]
Таким образом, страховой запас рассчитывается практически так же, как и границы интервального прогноза, т. е. формула для расчета страхового запаса аналогична формуле (7.8). [c.166]
На рис. 7.4 приведены нижняя и верхняя границы, определенные по формуле (7.16), при /3 = 0,9. [c.166]
Рассчитанное значение страхового запаса соответствует только одному дню наступления дефицита, а именно, согласно прогнозу, Т= 15. Для учета возможных нарушений срока поставки необходимо также при расчете страхового запаса оценить влияние задержки, связанной с выполнением заказа, в частности с транспортировкой. [c.167]
Рассчитаем величину страхового запаса при условии задержки на один день по сравнению с прогнозной оценкой Т= 15 дн., т. е. на 16-й дн. [c.167]
Интеграл (7.20) не выражается через элементарные функции, поэтому для расчетов можно воспользоваться численными методами и ЭВМ или специальными таблицами. Для нормальной функции распределения с параметрами среднее значение тх = 0 и sx = 1. [c.168]
На рис. 7.5 приведены графики нормальной функции распределения (б) и плотности нормального распределения (а). [c.168]
Появление дефицита означает, что текущая величина запаса на складе равна нулю, т. е. у = 0. [c.168]
Следовательно, для определения вероятности отсутствия дефицита необходимо по формуле (7.9) рассчитать х = —- и по табл. 7.10 с пост мощью х найти Р(х). [c.169]
По табл. 7.10 находим Р(Т= 13) 0,999, т. е. вероятность дефицита ничтожно мала. [c.170]

Вернуться к основной статье