Таблицы распределений и их применение

из "Вводный курс эконометрики "

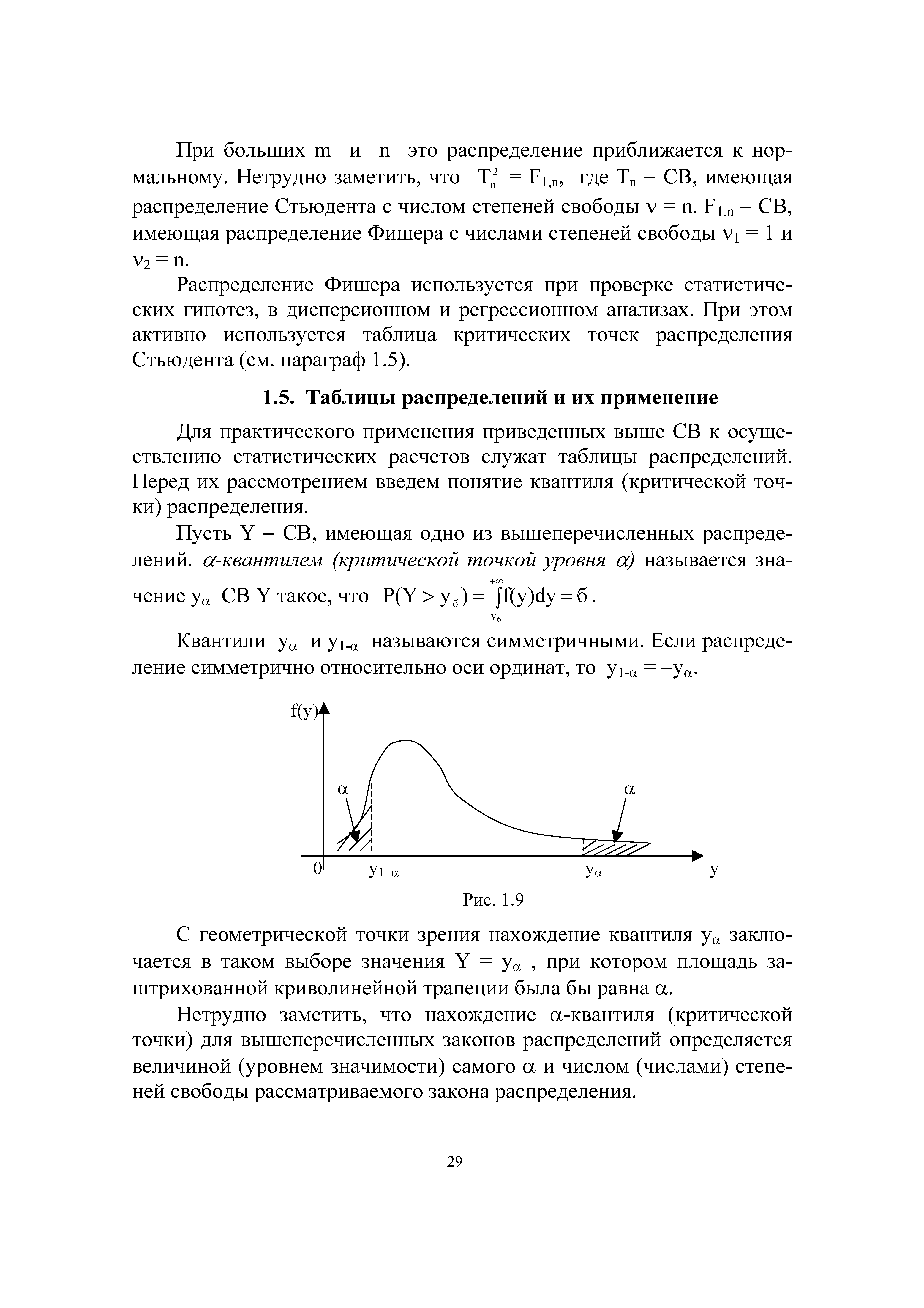
Для практического применения приведенных выше СВ к осуществлению статистических расчетов служат таблицы распределений. Перед их рассмотрением введем понятие квантиля (критической точки) распределения. [c.29]
С геометрической точки зрения нахождение квантиля уа заключается в таком выборе значения Y = ya, при котором площадь заштрихованной криволинейной трапеции была бы равна а. [c.29]
Нетрудно заметить, что нахождение a-квантиля (критической точки) для вышеперечисленных законов распределений определяется величиной (уровнем значимости) самого а и числом (числами) степеней свободы рассматриваемого закона распределения. [c.29]
В левом столбце таблицы приведены значения СВ U с точностью до десятых, в верхней строке приведены сотые доли U (значения U в данном случае определяются с точностью до сотых). Значение Ф(и) определяется на пересечении соответствующих данному значению и строки и столбца (в данном случае Ф(и) дается с точностью до четвертого знака после запятой). Например, Ф(0.17) = 0.0675, т. е. P(0 U 0.17) = 0.0675. Суть функции Лапласа Ф(и) и ее связь с функцией распределения F(u) стандартизированной нормальной СВ представлена на рис. 1.10. [c.30]
Отметим, что каждое значение F(u) больше соответствующего значения Ф(и) ровно на 0.5. Поэтому ее таблицы имеют аналогичный вид. [c.31]
В данной таблице в первом столбце указаны числа степеней свободы v. В верхней строчке указаны вероятности (уровни значимости) а. Критическая точка ta v определяется пересечением столбца с заданной вероятностью а и строки, соответствующей числу степеней свободы v. Например, t0.o5 io = 1.812. Другими словами, P(tio 1.812) = 0.05. [c.31]

Вернуться к основной статье