Формализация качественных характеристик

из "Ситуационное управление теория и практика "

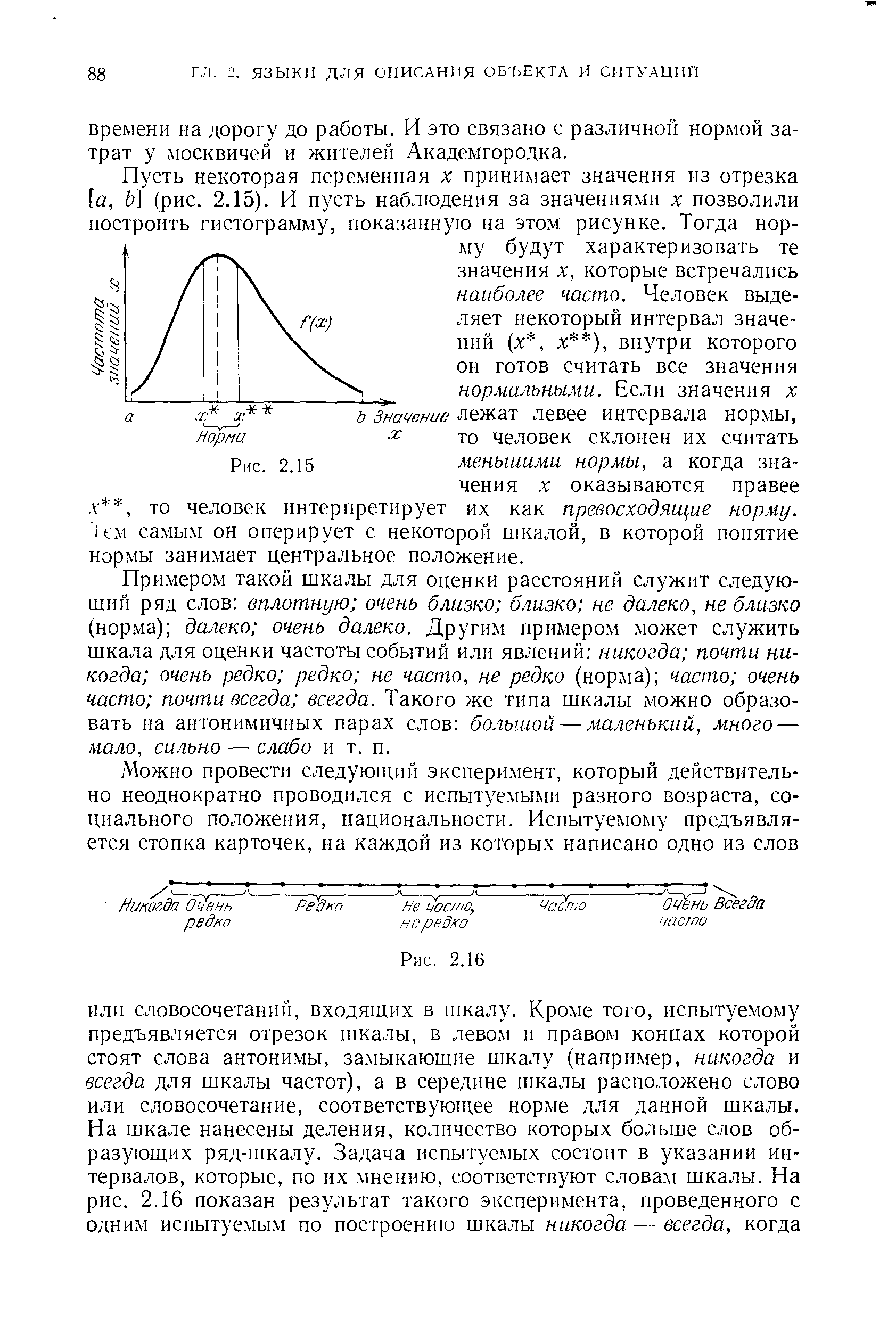
Примером такой шкалы для оценки расстояний служит следующий ряд слов вплотную очень близко близко не далеко, не близко (норма) далеко очень далеко. Другим примером может служить шкала для оценки частоты событий или явлений никогда почти никогда очень редко редко не часто, не редко (норма) часто очень часто почти всегда всегда. Такого же типа шкалы можно образовать на антонимичных парах слов большой — маленький, много — мало, сильно — слабо и т. п. [c.88]
Понятие функции принадлежности, которое возникло у нас в связи с обработкой экспериментального материала, может быть задано вполне строго. [c.89]
Функцией принадлежности для некоторого множества W называется функция ц(ау), определенная на всех элементах множества W = W и принимающая значения из отрезка [0,1]. [c.89]
Смысл этого определения можно интерпретировать следующим образом. Если для некоторого w W ц(ш)=0, то это означает, что w не принадлежит IF если для некоторого w W ц(ш ) = 1, то w принадлежит W. Если же для некоторого w 0 ц(ш) 1, то это означает, что w принадлежит W с некоторой возможностью, оцениваемой величиной [i(w). [c.89]
Отсюда вытекает способ выбора а, обеспечивающий отнесение всех значений на шкале к некоторому единственному множеству. [c.91]
Рассмотрим теперь весьма важную проблему — проблему универсальной шкалы. Пока значения функций принадлежности будут целиком определяться семантикой некоторой конкретной проблемной области, трудно делать какое-либо общее заключение о шкалах или строить процедуры работы с ними. [c.91]
Если мы имеем другое событие пли явление со своей гистограммой /а(я), то истинные частоты его появления, оцениваемые как редкие, будут другими. На рис. 2.19 им соответствует отрезок [т]ь г 2], который не совпадает с отрезком [ ь t..,]. [c.91]
Опишем теперь иной подход к процессу введения универсальной шкалы. [c.92]
Отображение 1 можно задать в виде некоторой матрицы, в которой строкам соответствуют состояния wt, а столбцам — полные ситуации s . На пересечении строк и столбцов можно задать число O mjj l, которое будет характеризовать возможность замены Wi на s или обратной замены. Тогда строки матрицы можно рассматривать как функции принадлежности м ,- на множестве полных ситуаций. А столбцы матрицы — как функции принадлежности st на множестве истинных состояний объекта управления. [c.93]
Пример 2.17. Рассмотрим таблицу-матрицу 2.7. [c.93]
Здесь А и А — состояния некоторой среды, а В и В — связанные сними состояния модели, отображающей эту среду. Операторам преобразования Т в среде должны согласованно соответствовать операторы преобразования в модели Q. Для успешности моделирования необходимо, чтобы диаграмма моделирования была коммутативной. [c.94]
Такой линейный сдвиг, наблюдавшийся в описанном выше примере, позволяет выдвинуть весьма важную гипотезу о том, что изменение семантики ситуаций, в которых производится оценка расстояний, приводит к гомоморфному отображению функции принадлежности. Другими словами, если шкалы, на которых заданы наши функции принадлежности или нечеткие интервалы, преобразовать линейно с помощью функции у=ах—Ь, то функции принадлежности не меняются, а меняется лишь семантика той ситуации, к которой они относятся. Высказанная гипотеза должна найти подтверждение в экспериментах с людьми для различных по интерпретации отношений моделирования (пока она проверялась лишь для отношения расстояния). Если эксперименты подтвердят ее, то работа с качественными описаниями существенно упростится. [c.95]
Перечислим в заключение параграфа те задачи, в решении которых нечеткое отношение моделирования может сыграть важную роль. [c.95]

Вернуться к основной статье