Оптимизация сетевых моделей

из "Оптимальное управление экономическими системами "

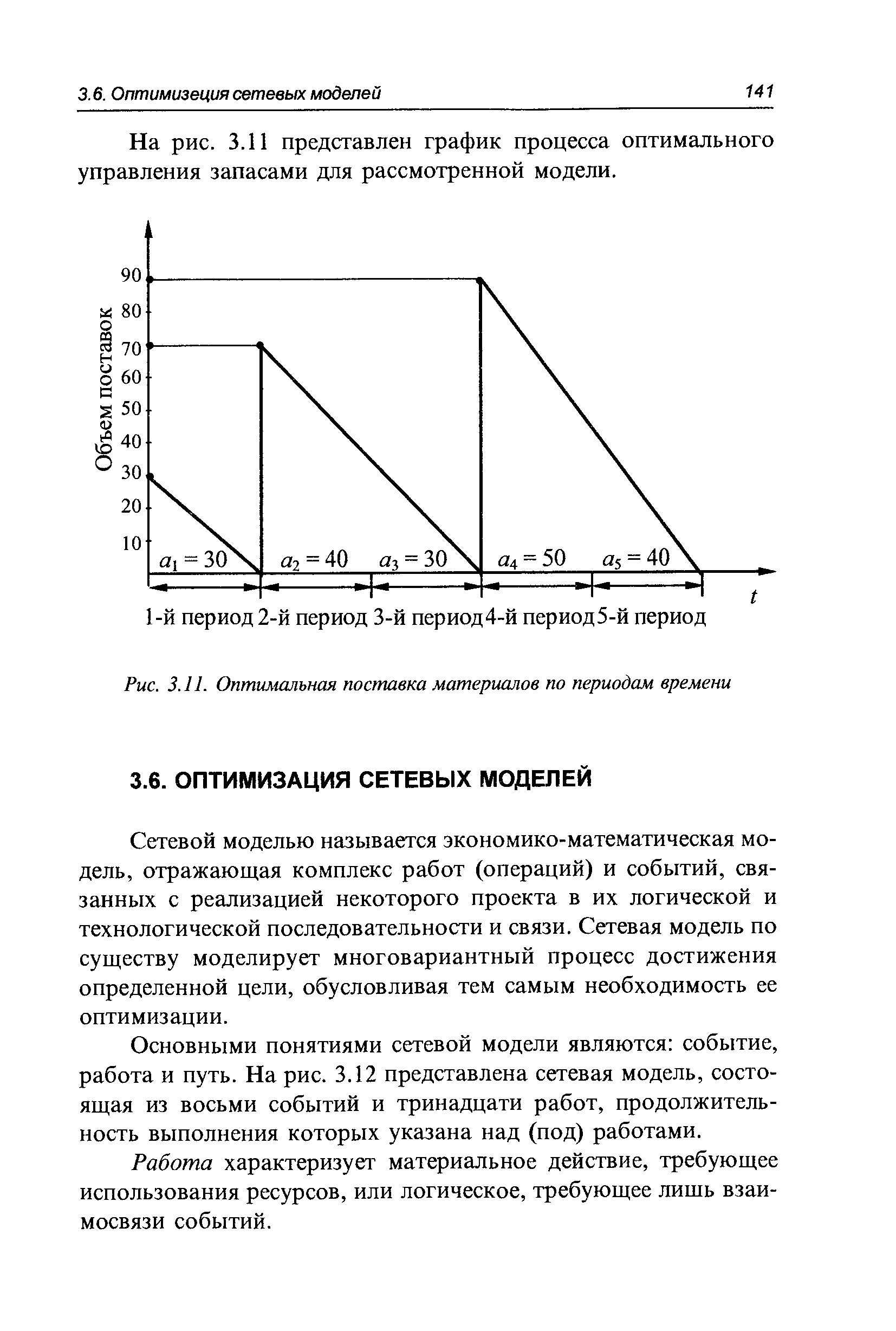
На рис. 3.11 представлен график процесса оптимального управления запасами для рассмотренной модели. [c.141]
Сетевой моделью называется экономико-математическая модель, отражающая комплекс работ (операций) и событий, связанных с реализацией некоторого проекта в их логической и технологической последовательности и связи. Сетевая модель по существу моделирует многовариантный процесс достижения определенной цели, обусловливая тем самым необходимость ее оптимизации. [c.141]
Основными понятиями сетевой модели являются событие, работа и путь. На рис. 3.12 представлена сетевая модель, состоящая из восьми событий и тринадцати работ, продолжительность выполнения которых указана над (под) работами. [c.141]
Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий. [c.141]
Глава 3. Применение экономико-математических моделей.. [c.142]
Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени и свершаются в тот момент, когда оканчивается последняя из работ, входящая в него. [c.142]
Путь — это последовательность работ, соединяющих начальную и конечную точки вершины. [c.142]
Кстати, путь, имеющий максимальную продолжительность, называется критическим определение его параметров представляет собой центральную проблему сетевого управления экономическими системами. [c.142]
Рассмотренные нами методы математического моделирования достаточно эффективно могут быть использованы при расчете различных параметров сетевых моделей и, в частности, критического пути. Проиллюстрируем это утверждение на примере расчета критического пути в приведенной на рис. 3.12 сетевой модели. [c.142]
С учетом вышесказанного для читателя должно быть очевидно, что наиболее эффективным при решении данной задачи будет использование аппарата динамического программирования. [c.142]
События сетевой модели целесообразно в этом случае упорядочить по этапам решения задачи, используя для этого следующий алгоритм. [c.142]
Работу данного алгоритма можно наглядно проиллюстрировать при помощи нижеприведенной таблицы. [c.143]
Трансформированный таким образом (под метод динамического программирования) сетевой график будет иметь следующий вид (рис. 3,13). [c.143]
Таким образом, критическим в рассмотренной сетевой модели является путь через события 1, 3, 7, 8 с общей продолжительностью 15 единиц. [c.145]

Вернуться к основной статье