Концепция доминирования

из "Микроэкономика-третий уровень "

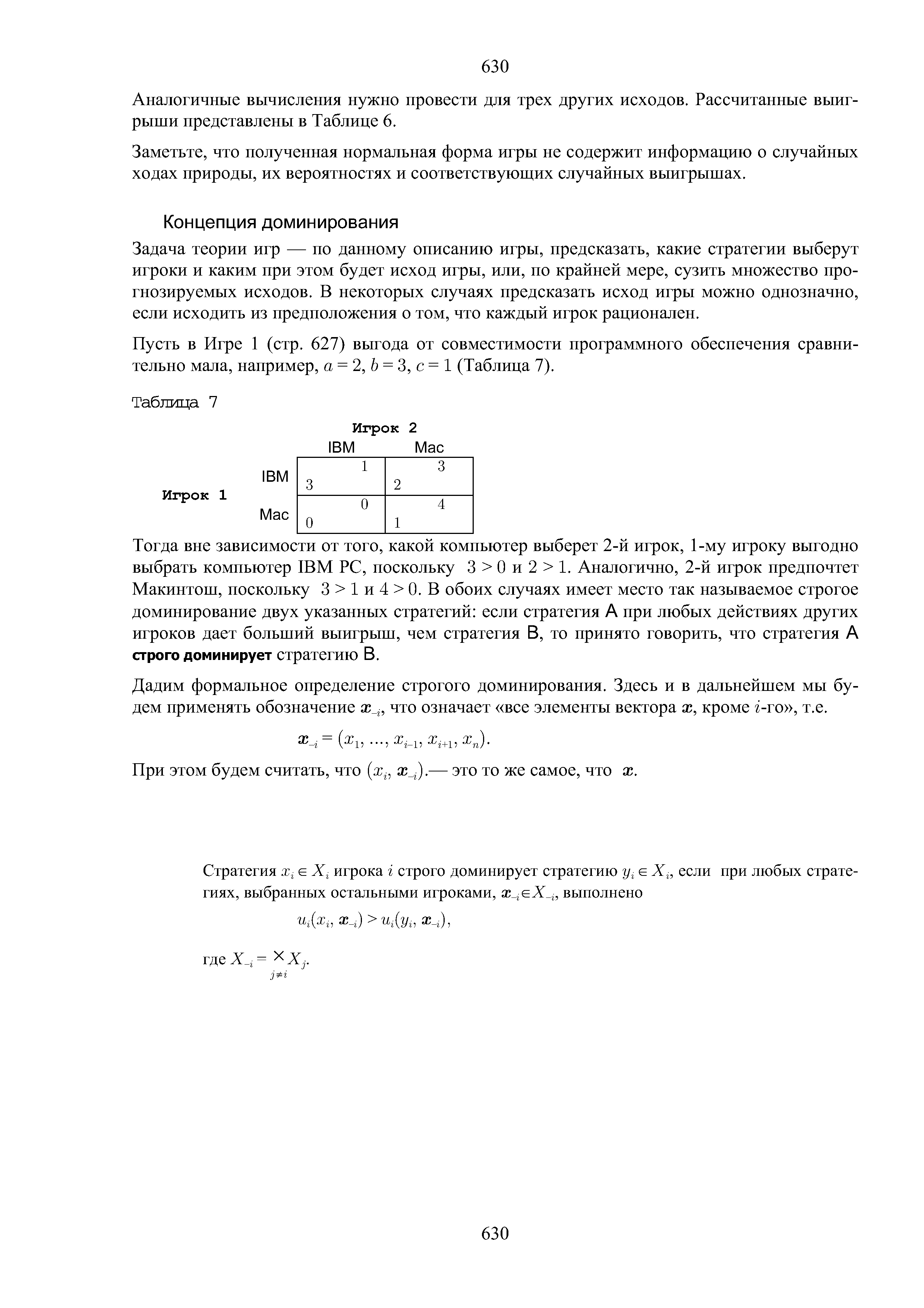
Задача теории игр — по данному описанию игры, предсказать, какие стратегии выберут игроки и каким при этом будет исход игры, или, по крайней мере, сузить множество прогнозируемых исходов. В некоторых случаях предсказать исход игры можно однозначно, если исходить из предположения о том, что каждый игрок рационален. [c.630]
Пусть в Игре 1 (стр. 627) выгода от совместимости программного обеспечения сравнительно мала, например, а = 2,5 = 3,с=1 (Таблица 7). [c.630]
Тогда вне зависимости от того, какой компьютер выберет 2-й игрок, 1-му игроку выгодно выбрать компьютер IBM P , поскольку 3 0 и 2 1. Аналогично, 2-й игрок предпочтет Макинтош, поскольку 3 1и4 О.В обоих случаях имеет место так называемое строгое доминирование двух указанных стратегий если стратегия А при любых действиях других игроков дает больший выигрыш, чем стратегия В, то принято говорить, что стратегия А строго доминирует стратегию В. [c.630]
Дадим формальное определение строгого доминирования. Здесь и в дальнейшем мы будем применять обозначение х г, что означает все элементы вектора х, кроме г-го , т.е. [c.630]
При этом будем считать, что (жг, ж г). — это то же самое, что х. [c.630]
Определение строгого доминирования можно наглядно проиллюстрировать в случае двух игроков, множества стратегий одного из которых — действительная прямая (см. Рис 149). На рисунке стратегия xl первого игрока строго доминирует стратегию уг. Это выражается в том, что график функции полезности этого игрока по стратегии х2 второго, соответствующий ж1 лежит ниже графика, соответствующего уг. [c.631]
Стратегия называется строго доминирующей, если она строго доминирует любую другую стратегию. [c.631]
Стратегия хг е Хг игрока г является его строго доминирующей стратегией, если при любых стратегиях, выбранных остальными игроками, х г е Х г, она дает игроку г больший выигрыш, чем любая другая его стратегия уг е Хг, т.е. [c.631]
В соответствие с данным определением не может существовать более одной строго доминирующей стратегии. Естественно ожидать, что рациональный игрок выберет именно такую стратегию. Поэтому при наличии у каждого игрока строго доминирующей стратегии исход игры может быть предсказан однозначно. [c.631]
Предсказание исхода игры не столь однозначно, когда у каждого игрока имеется лишь так называемая (слабо) доминирующая стратегия, обеспечивающая этому игроку не меньший выигрыш, чем любая другая его стратегия при любых стратегиях других игроков. Приведем определения (слабого) доминирования. [c.631]
Слабое доминирование можно проиллюстрировать на графике, аналогичном тому, который мы использовали для иллюстрации строгого доминирования. Стратегия xl первого игрока слабо, но не строго доминирует его стратегию у1 (см. Рис. 150), поскольку график функции полезности для х1 не везде строго выше, чем для у . [c.632]
Из определения следует, что если стратегия хг строго доминирует стратегию уг, то стратегия хг доминирует стратегию уг. Кроме того, если стратегия является строго доминирующей, то она является доминирующей. [c.632]
Исход игры х е X является равновесием в доминирующих стратегиях, если стратегия каждого игрока в этом исходе является его доминирующей стратегией. [c.632]
Естественно ожидать, что если в игре существует равновесие в доминирующих стратегиях, то именно оно будет реализовавшимся исходом игры. Следующая игра иллюстрирует равновесие в доминирующих стратегиях. [c.632]
Удобно представить исходы игры в виде двух таблиц А и Б (см. Таблицу 8). Белые выбирают между таблицей А и таблицей Б. Их выигрыши записаны в левом верхнем углу этих таблиц. [c.633]
Если зеленые проголосуют за, то вектор их выигрышей будет (1 (за, за), 1 (за, против), 1 (против, за), 0 (против, против)). [c.633]
Очевидно, что голосовать за законопроект является доминирующей стратегией зеленых. То же самое можно сказать и о красных. [c.633]
Таким образом, голосовать против законопроекта является доминирующей стратегией белых (хотя, заметим, эта стратегия не сможет им помочь выиграть). [c.633]
Тем самым, в этой игре существует равновесие в доминирующих стратегиях. В нем зеленые и красные голосуют за , а белые — против . [c.633]
Приведем теперь пример игры с непрерывными стратегиями, в который есть равновесие в доминирующих стратегиях. [c.633]

Вернуться к основной статье