Комбинации (двойные и тройные тройки)

из "Код эллиота волновой анализ рынка forex "

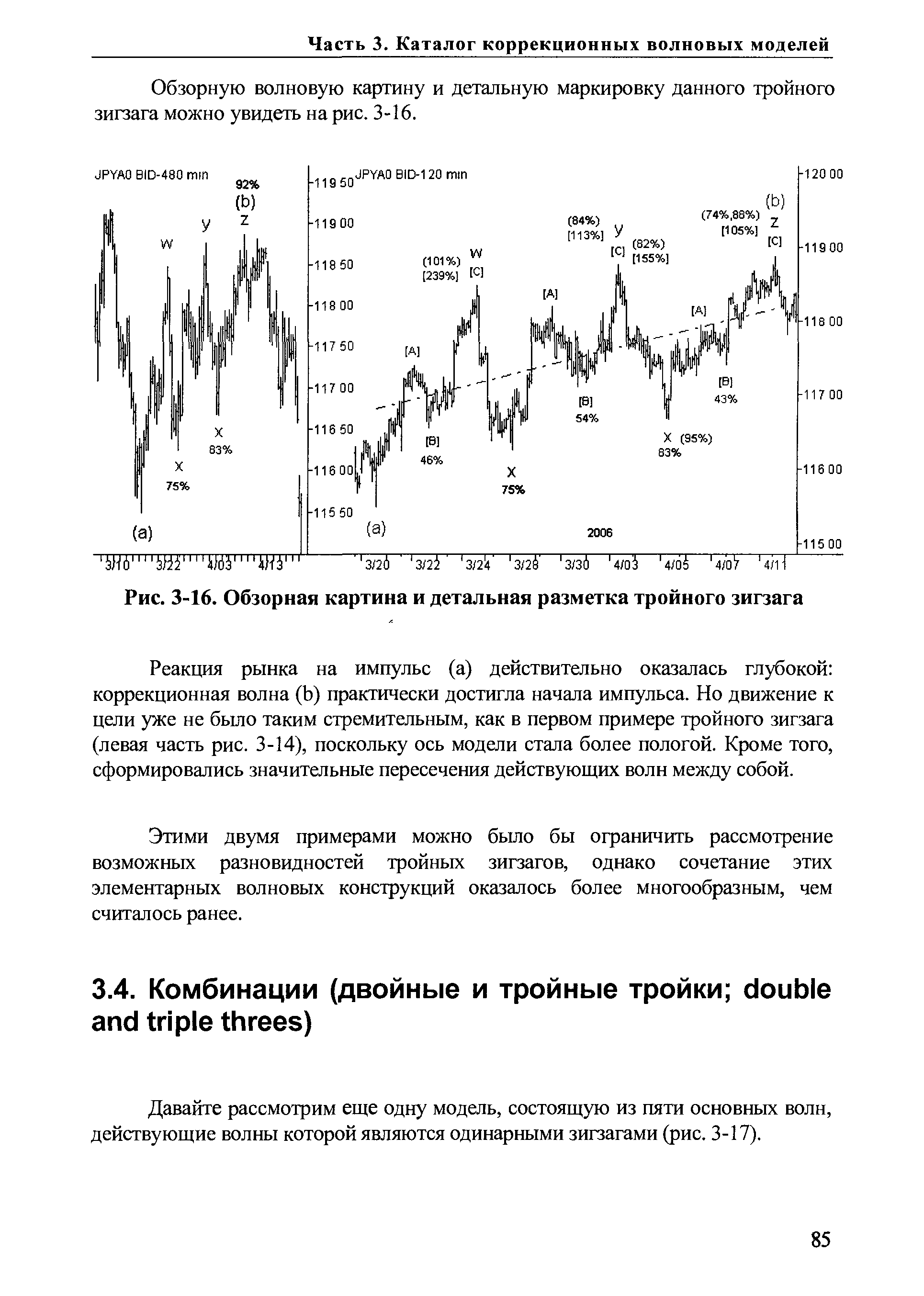
Давайте рассмотрим еще одну модель, состоящую из пяти основных волн, действующие волны которой являются одинарными зигзагами (рис. 3-17). [c.85]
В этом примере развитие модели идет практически горизонтально (волна (iv)) с небольшим наклоном против доминирующего тренда старшего уровня (волна (iii)). Все действующие волны w, у и z данной модели — зигзаги. Они объединены в единую структуру волнами-связками х, которые также являются зигзагами. [c.87]
Несомненно, формула модели — 3-3-3-3-3, и по составу действующих волн модель может быть тройным зигзагом. Но посмотрите, насколько она отличается от двух предыдущих примеров (рис. 3-13..3-16). На обзорном рис. 3-18 хорошо видно, что данная коррекция не является глубокой. [c.87]
Действительно, отличительной чертой данной модели является ее горизонтальность, которая и перечеркивает все задачи, традиционно возлагаемые на двойные/тройные зигзаги. [c.87]
Такое упорство было похоже на попытку втиснуть в существующие рамки классификации коррекций новые разновидности волновых моделей, в том числе и с новых рынков. Ведь ни для кого не секрет, что рынок FX совсем молод по сравнению с фондовым рынком, он появился только в начале 70-х годов прошлого века. Кроме того, рынок FX обладает своими индивидуальными особенностями, которые оказывают влияние на внешнюю форму и структуру волновых моделей. [c.87]
Для решения этой небольшой проблемы классификации коррекций есть несколько путей. Во-первых, можно называть все модели с тремя действующими волнами в виде зигзагов тройными зигзагами, независимо от наклона оси модели. Остальные модели с формулой 3-3-3-3-3 можно отнести к тройным тройкам. Но в этом случае задачи, традиционно возлагаемые на тройные зигзаги, будут вносить постоянную сумятицу в анализ волновой картины в случае горизонтального развития подобной волновой структуры. [c.87]
В-третьих (и самое логичное с моей точки зрения), можно вернуться к варианту, предложенному первооткрывателем Закона волн, но, видимо, незаслуженно забытому или модифицированному до неузнаваемости в попытке строгой классификации моделей. Идея Эллиотта состояла в том, чтобы глубокие коррекции, действующие волны которых состоят из одних зигзагов относить к классу двойных зигзагов (здесь просто необходимо дополнение Фроста и Пректера— тройные зигзаги). Все остальные модели, независимо от типа действующих волн, но формирующихся практически горизонтально или с небольшим наклоном против предшествующего тренда, относить к двойным/тройным тройкам. Ведь сам Эллиотт ни словом не обмолвился о возможном составе таких моделей, тройки — и все. [c.88]
Конечно, столь неточный признак, как небольшой наклон не позволит провести однозначную грань между двойными/тройными зигзагами и двойными/тройными тройками, состоящими из зигзагов, но так ли уж это принципиально В конце концов, пусть у аналитика остается некоторая свобода выбора. [c.88]
Таким образом, комбинации или как их называл Эллиотт сложные коррекции представляют собой сочетание, комбинацию (извините за тавтологию) элементарных коррекционных моделей — троек (о некоторых ограничениях, все-таки накладываемых на состав волн, поговорим немного позже). Сама модель формируется горизонтально или с небольшим наклоном против предшествующего тренда. По количеству входящих в комбинацию троек различаются двойные тройки и тройные тройки. Сами понимаете, что одинарная тройка— это любая элементарная волновая конструкция, то есть зигзаг или плоскость. [c.88]
Задача комбинаций, в отличие от задач, возлагаемых на двойные/тройные зигзаги, состоит в том, чтобы после того, как ее первой действующей волной был достигнут необходимый по глубине ценовой рубеж, создать коррекцию, адекватную по длительности предыдущему тренду. Действительно, если тройная тройка является четвертой волной импульса, как на рис. 3-18, то она должна быть сравнима по длительности со второй волной импульса, чего невозможно достичь только ее первой действующей волной w. Вот и приходится коррекционной модели удваивать и утраивать по длительности свою конструкцию. [c.88]
Другой известный аналитик Роберт Балан, специализирующийся на рынке FX, в своей книге привел более двух десятков схематичных изображений двойных и тройных троек, состоящих из различных элементарных конструкций. С моей точки зрения, он изобразил большую часть возможных сочетаний элементарных фигур в моделях старшего уровня, но в качестве реального примера привел лишь один тройной зигзаг на месте волны С в растянутой волновой плоскости (это его находка, о которой поговорим в разделе 5.1. Возможные исключения из правил ). [c.89]
Не стану отрицать возможность различных допустимых сочетаний элементарных форм в моделях старшего уровня, так как интересные экземпляры сложных коррекций действительно встречаются. И надо быть готовым увидеть на реальном рынке все теоретически допустимые варианты. Не буду отрицать возможности такого (и даже большего) многообразия двойных и тройных троек, которые в своей книге привел Балан. Но смею утверждать, что на реальном рынке FX действующие волны подавляющего большинства составных коррекций (двойных/тройных троек и треугольников) являются зигзагами (в основном одинарными, реже — двойными). О двойных/тройных зигзагах нет смысла говорить, так как их действующие волны по определению являются только зигзагами. [c.89]
тройная тройка представляет собой коррекционную модель с формулой 3-3-3-3-3 и сильно пересекающимися между собой действующими волнами. Образующие линии модели, проведенные через вершины w-y и х-х, могут быть обе наклонены против предшествующего тренда или в разные стороны, а также могут быть горизонтальными. В соответствии с формулой ее действующие волны могут представлять собой любую коррекционную модель с учетом небольших ограничений, о которых поговорим немного позже. [c.89]
Начальный вариант правил для тройных троек выглядит следующим образом. [c.89]
Реальный пример данной модели, у которой одна действующая волна является плоскостью, представлен на рис. 3-19. [c.90]
Действительно, волна Y данной модели— волновая плоскость. Первая волна-связка X также является растянутой волновой плоскостью, но сейчас нас интересуют только действующие волны. Кстати, среди волн-связок внутри составных коррекций волновые плоскости встречаются гораздо чаще, чем на месте действующих волн. [c.90]
На обзорной картине (рис. 3-20) хорошо видно, что сама тройная тройка является волной (а) сдвигающейся волновой плоскости, форму которой приняла волна [iv] импульса (см. раздел 3.6.). [c.90]
Поскольку для прояснения ситуации с тройными коррекциями требовались примеры коррекций именно с пятью основными волнами, то данный раздел и был начат с тройных троек. Теперь пора привести несколько образцов более простых волновых конструкций — двойных троек. [c.90]
Если рассмотреть этот участок графика на более мелком тайм-фрейме (например, на 120 мин), то нетрудно увидеть, что волна iv of (a) of [x] также является двойной тройкой, состоящей из одних зигзагов. [c.92]

Вернуться к основной статье