Чередование в коррекционных моделях

из "Код эллиота волновой анализ рынка forex "

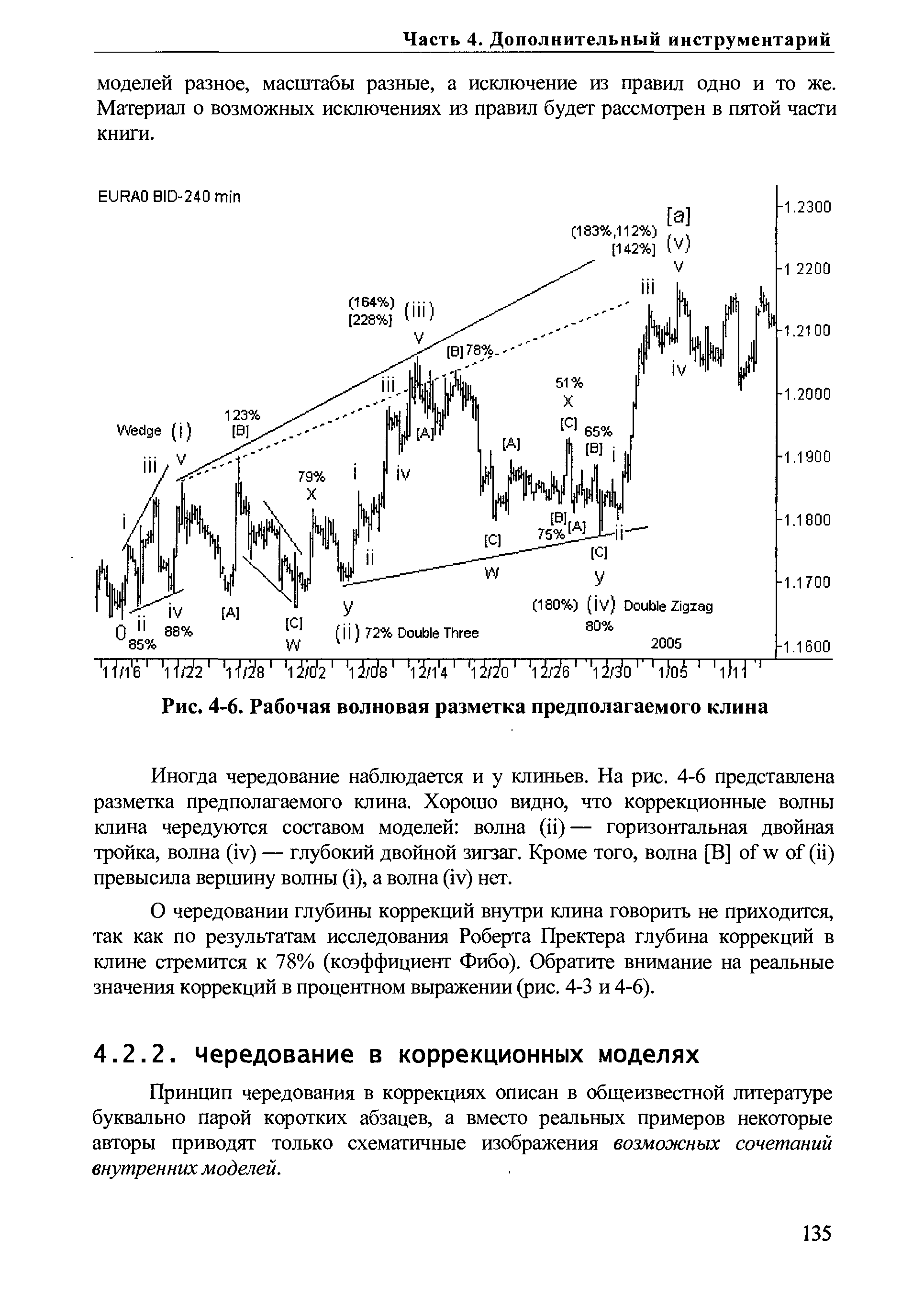
Принцип чередования в коррекциях описан в общеизвестной литературе буквально парой коротких абзацев, а вместо реальных примеров некоторые авторы приводят только схематичные изображения возможных сочетаний внутренних моделей. [c.135]
Большая часть этих кратких сообщений посвящена чередованию волн внутри волновой плоскости. Действительно, эта модель оказалась наиболее изменчивой из всех коррекций в плане чередования. Поскольку формула плоскости равна 3-3-5, то чередование может проявляться, прежде всего, в формировании различных типов коррекций на месте ее первых волн. Если первым формируется зигзаг в качестве волны А, то волна В может быть волновой плоскостью. Если первым формируется плоскость в качестве волны А, то волна В может быть зигзагом. [c.136]
В то же время, проанализировав не один километр графиков, смею утверждать, что у подавляющего большинства волновых плоскостей на рынке FX первые две волны являются зигзагами или их производными. [c.136]
Однако коррекционным моделям присуще также чередование по сложности волновых конструкций. Поскольку элементарная волновая модель состоит из трех волн, то можно выделить три степени их возможной сложности Простая—Сложная—Самая Сложная (П-С-СС). В данном случае термин сложность подразумевает не только замысловатость конструкции, но и ее размашистость и длительность. Конечно, подобное деление достаточно условно и субъективно, но в 90% случаев оно весьма действенно. Некоторые реальные примеры волновых плоскостей с различными сочетаниями внутренних моделей рассмотрим далее. [c.136]
Волновая плоскость на рис. 4-7 начинается с растянутой волновой плоскости, затем следуют зигзаг и импульс. Налицо классический пример чередования. По сложности ее можно отнести к категории СС-С-П. Волна a of (iv) сама представляет собой растянутую волновую плоскость, но состоит из традиционного набора волн для плоскостей зигзаг, зигзаг, импульс. По сложности составных волн ее также можно отнести к категории СС-С-П. [c.137]
На рис. 4-8 волновая плоскость состоит из волновой плоскости, двойного зигзага и импульса. Категория СС-С-П. Волна (a) of [ii] представляет собой самый распространенный состав внутренних волн для плоскостей пара зигзагов и импульс. Все ее составные волны приблизительно одного уровня сложности. [c.137]
Плоскость на рис. 4-9 начинается с тройного зигзага, затем идет плоскость и завершает модель не самый стройный импульс. Категория сложности — С-СС-П. Волна (b) of [ii] представляет собой волновую плоскость с традиционным набором волн, которые являются приблизительно одинаковыми по сложности. [c.137]
Кроме того, несколько примеров волновых плоскостей с наиболее обычными по составу внутренними моделями можно увидеть в предыдущей части книги на рис. 3-5 (категория П-С-СС), 3-7 (категория С-СС-П), 3-9 (категория С-СС-П), а также на рис. 4-6 (плоскость w of (ii), категория С-П-СС). [c.137]
Если составить перечень возможных неповторяющихся сочетаний категорий сложности, то получим всего шесть комбинаций + модель с волнами приблизительно одинаковой сложности (табл. 4-2). [c.138]
Приблизительно одного уровня сложности (а) на 4-8, (Ь) на 4-9. [c.138]
Мне пока не удалось найти на рынке FX однозначных примеров плоскостей, которые начинаются с пары резкого контраста (Простой — Самый Сложный) или (Самый Сложный — Простой). Возможно, мне просто не улыбнулась удача. Однако не исключено, что это сочетание является слишком тяжелым для начала модели. [c.139]
Волновых плоскостей, которые заканчиваются простым, кратким по длительности и глубоким импульсом С на рынке FX сколько угодно, даже, если перед ним стоит самая замысловатая волна В. Именно такие модели дали основание присвоить волнам С характеристику разрушительных волн (например, волна (С) of [В] на рис. 3-7). Кроме того, есть редкие примеры моделей, которые заканчиваются контрастной парой (Простой — Самый Сложный), но не начинаются с нее, см. рисунок 4-6, плоскость w of (ii) и рисунок 4-10. [c.139]
Правда, в некоторых, не столь уж редких случаях зигзаг все же старается проявить принцип чередования, формируя одну свою ногу сложнее, изощреннее, чем другую. Примером может служить зигзаг (а)-(Ь)-(с) на рис. 3-9 или зигзаг а-Ь-с на рис. 3-36, когда волны данной модели последовательно наращивают свою сложность. Но подобное чередование не получило широкого распространения на финансовых рынках. [c.140]
О чередовании в двойной тройке или протяженных коррекциях (в том числе и горизонтальных треугольниках) достоверно можно утверждать только то, что одна волна данных моделей стремится быть сложнее, протяженнее других. Утверждение некоторых авторов о том, что соседние волны треугольников должны отличаться одна от другой, не подтверждается практикой подавляющее большинство волн двойных и протяженных коррекций — зигзаги (как правило, одинарные, реже — двойные). [c.140]
Таким образом, указание о чередовании может помочь в правильной волновой разметке и даже прогнозировании предполагаемой формы модели, но однозначного ответа на эти же вопросы оно дать не может. [c.140]

Вернуться к основной статье