Пример практического применения

из "Анализ финансовых данных "

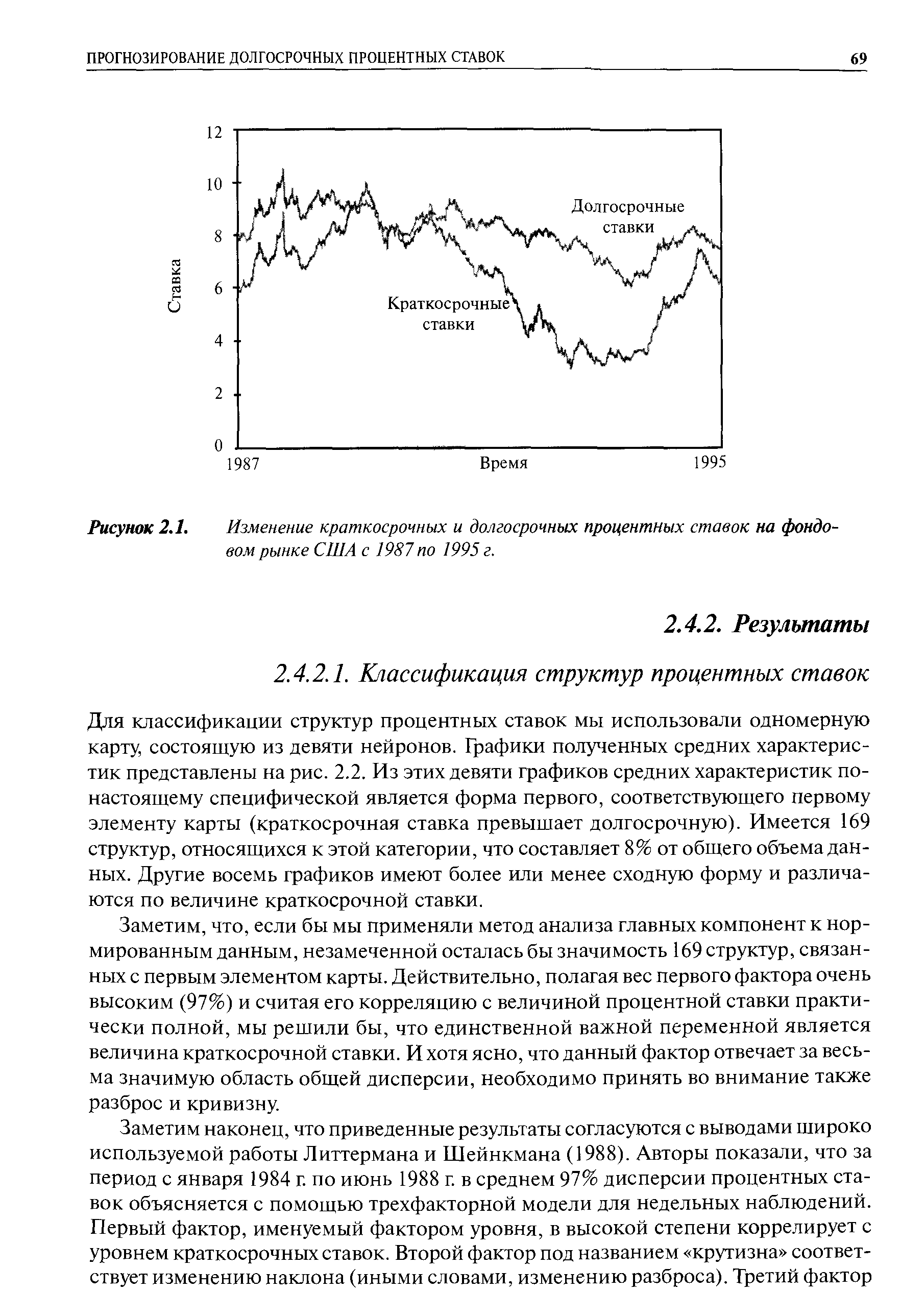
Для классификации структур процентных ставок мы использовали одномерную карту, состоящую из девяти нейронов. Графики полученных средних характеристик представлены на рис. 2.2. Из этих девяти графиков средних характеристик по-настоящему специфической является форма первого, соответствующего первому элементу карты (краткосрочная ставка превышает долгосрочную). Имеется 169 структур, относящихся к этой категории, что составляет 8% от общего объема данных. Другие восемь графиков имеют более или менее сходную форму и различаются по величине краткосрочной ставки. [c.69]
Заметим, что, если бы мы применяли метод анализа главных компонент к нормированным данным, незамеченной осталась бы значимость 169 структур, связанных с первым элементом карты. Действительно, полагая вес первого фактора очень высоким (97%) и считая его корреляцию с величиной процентной ставки практически полной, мы решили бы, что единственной важной переменной является величина краткосрочной ставки. И хотя ясно, что данный фактор отвечает за весьма значимую область общей дисперсии, необходимо принять во внимание также разброс и кривизну. [c.69]
Рисунок 2.2. Графики средних характеристик кластеризованных структур процентных ставок, построенные на основании ежедневных данных по фондовому рынку США (1987-1995). [c.70]
Рисунок 2.3. Графики средних характеристик кластеризованных скачков процентных ставок, построенные на основании ежедневных данных по фондовому рынку США (1987-1995). [c.71]
Как подчеркивалось во введении, рассматриваемый метод не требует априорного предположения об аналитическом виде процесса, определяющего текущую процентную ставку. Но если существует свойство возврата к среднему значению или связь между уровнем процентной ставки и дисперсией, наш метод будет это учитывать В сущности, мы рассматриваем величину скачков (дисперсию) по отношению к начальной структуре, подобно тому, как мы характеризовали соотношение между классом скачков процентной ставки и начальной структурой (состоянием процесса). Вероятность более значительного скачка процентной ставки будет меньше, если уровень начальной структуры высок, и наоборот (интуитивно понятно, что это является естественным следствием свойства возврата к среднему значению). Кроме того, поскольку мы не вводили ограничений для процесса, определяющего наблюдаемые переменные, мы надеемся воспроизвести статистические свойства исторического изменения структуры процентных ставок. [c.72]
Мы проверили девять условных эмпирических распределений скачков и всю их совокупность на статистическую независимость, используя критерий X2. Результаты приведены в табл. 2.3. Условные распределения скачков процентной ставки статистически отличаются от распределения всего множества скачков при очень высоком уровне значимости. Таким образом, существование связи между скачками и начальной структурой процентной ставки подтверждается эмпирически. [c.72]
На рис. 2.4 и 2.5 показаны соответственно распределения краткосрочных и долгосрочных процентных ставок, полученные в ходе трех процедур моделирования. Первые два раза использовалась одна и та же начальная форма процентной ставки (победителем в которой является элемент 6). В третий раз мы использовали исходную структуру процентных ставок, связанную с элементом 1 (единственная обратная средняя характеристика структуры процентных ставок). [c.74]
По виду этих графиков можно сказать, что процедура дает стабильные результаты и что, судя по моделированию для периода в пять лет, начальная структура процентных ставок влияет, главным образом, на уровень краткосрочных ставок. В каждом из случаев моделирования уровни краткосрочных и долгосрочных процентных ставок сопоставимы с их историческими значениями. На рис. 2.5 представлены пять структур процентных ставок, выбранных случайным образом из 1000 структур, полученных при первом моделировании. На рис. 2.6 представлены пути соответственно для краткосрочной и долгосрочной процентной ставки за 5 лет (по одному для каждой), полученные при первом моделировании. Очевидно, что они представляют собой возможные пути процентных ставок. Нам следует также отметить, что значения всех прогнозируемых процентных ставок положительны во всех случаях моделирования и на всех его этапах. [c.74]

Вернуться к основной статье