Системы массового обслуживания

из "Моделирование и управление в экономике Часть 1 "

Разыграв определенные значения случайных факторов, мы имеем возможность рассчитать конкретную случайную реализацию. [c.93]
Замечание. Большинство приложений метода Монте-Карло связано именно с имитацией. Замечание. Основная область применения этих методов - нейтронная физика. [c.93]
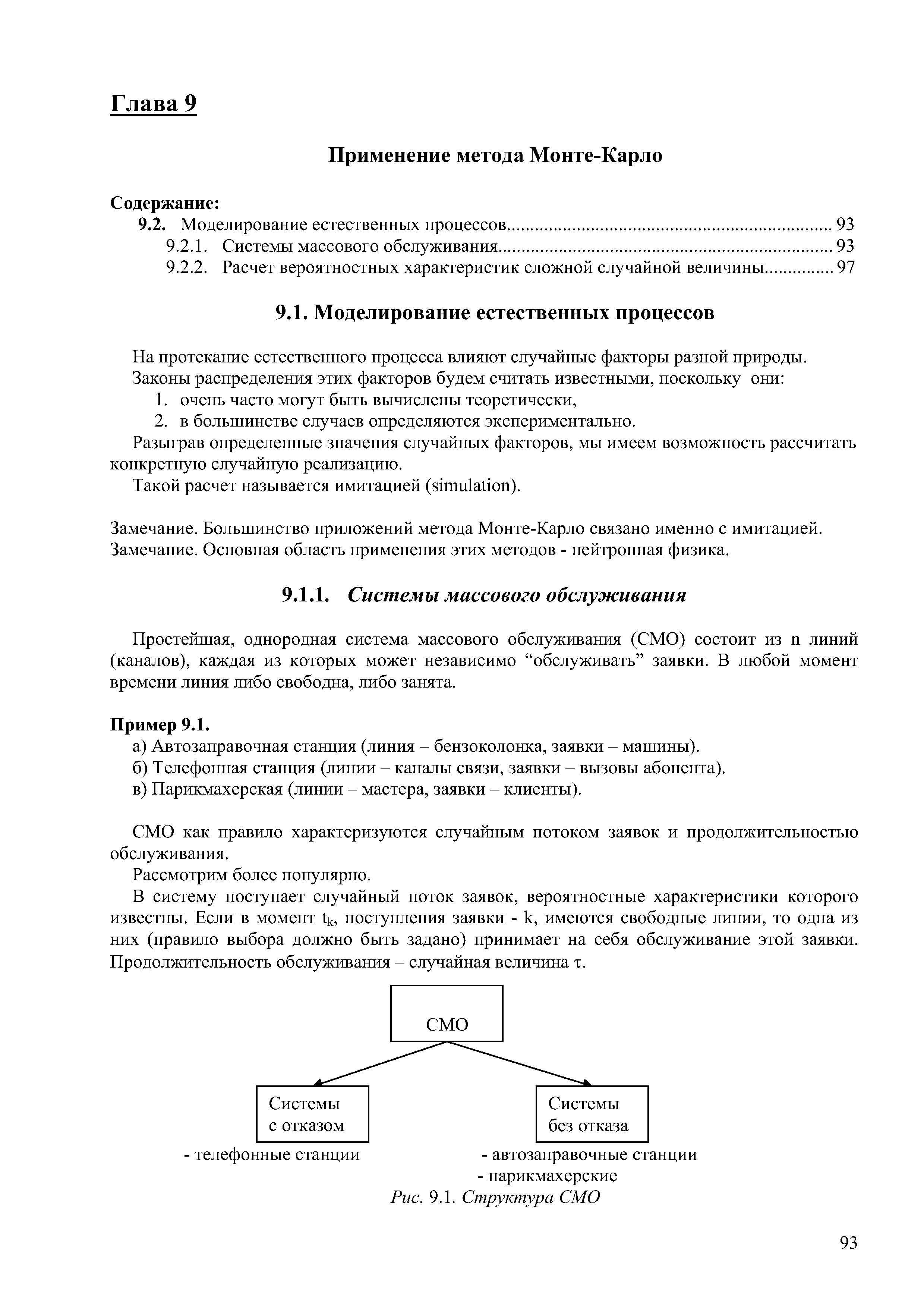
Простейшая, однородная система массового обслуживания (СМО) состоит из п линий (каналов), каждая из которых может независимо обслуживать заявки. В любой момент времени линия либо свободна, либо занята. [c.93]
СМО как правило характеризуются случайным потоком заявок и продолжительностью обслуживания. [c.93]
Рассмотрим более популярно. [c.93]
В систему поступает случайный поток заявок, вероятностные характеристики которого известны. Если в момент t , поступления заявки - k, имеются свободные линии, то одна из них (правило выбора должно быть задано) принимает на себя обслуживание этой заявки. Продолжительность обслуживания - случайная величина т. [c.93]
Важнейшая характеристика систем с отказами это среднее число отказов в заданном интервале времени. [c.94]
Естественно, число отказов зависит от поступающего потока заявок. [c.94]
Интенсивность такого потока равна--— —. [c.94]
Рассмотрим алгоритм расчета систем с отказом (п линий, P (t)). [c.94]
Правило выбора свободной линии сформулируем так заявка поступает на линию, которая освободилась раньше всех, а если таких несколько, то на ту из них, номер которой меньше. [c.95]
Линия 1 будет занята до момента TI новое =ti+ii Следовательно, в соответствующей первой линии ячейке, надо заменить TI на TI новое и вычислить новое Т. [c.95]
Затем вычисляется Т. —t,+T,n новое значение Т. [c.95]
После этого можно перейти к рассмотрению следующей (k+l)-oft заявки. [c.95]
В действительности, параметры всех деталей несколько отличаются от номинальных, и потому значения U для разных экземпляров прибора будут отличаться от ( ). [c.96]
Можно пытаться оценить пределы изменения U, выбирая самые неблагоприятные значения параметров. Однако не всегда ясно, какой набор параметров будет наихудшим. Как правило, такая оценка большого практического значения не имеет, так как на практике маловероятно, чтобы все параметры одновременно были наихудшими. [c.96]
Поэтому более рационально считать параметры всех деталей (сопротивления и емкости) независимыми случайными величинами и определить закон распределения случайной величины U. [c.97]
Для такого расчета необходимо знать функции распределения параметров всех деталей. Вероятностные характеристики деталей заводами-изготовителями не выдаются. [c.97]

Вернуться к основной статье