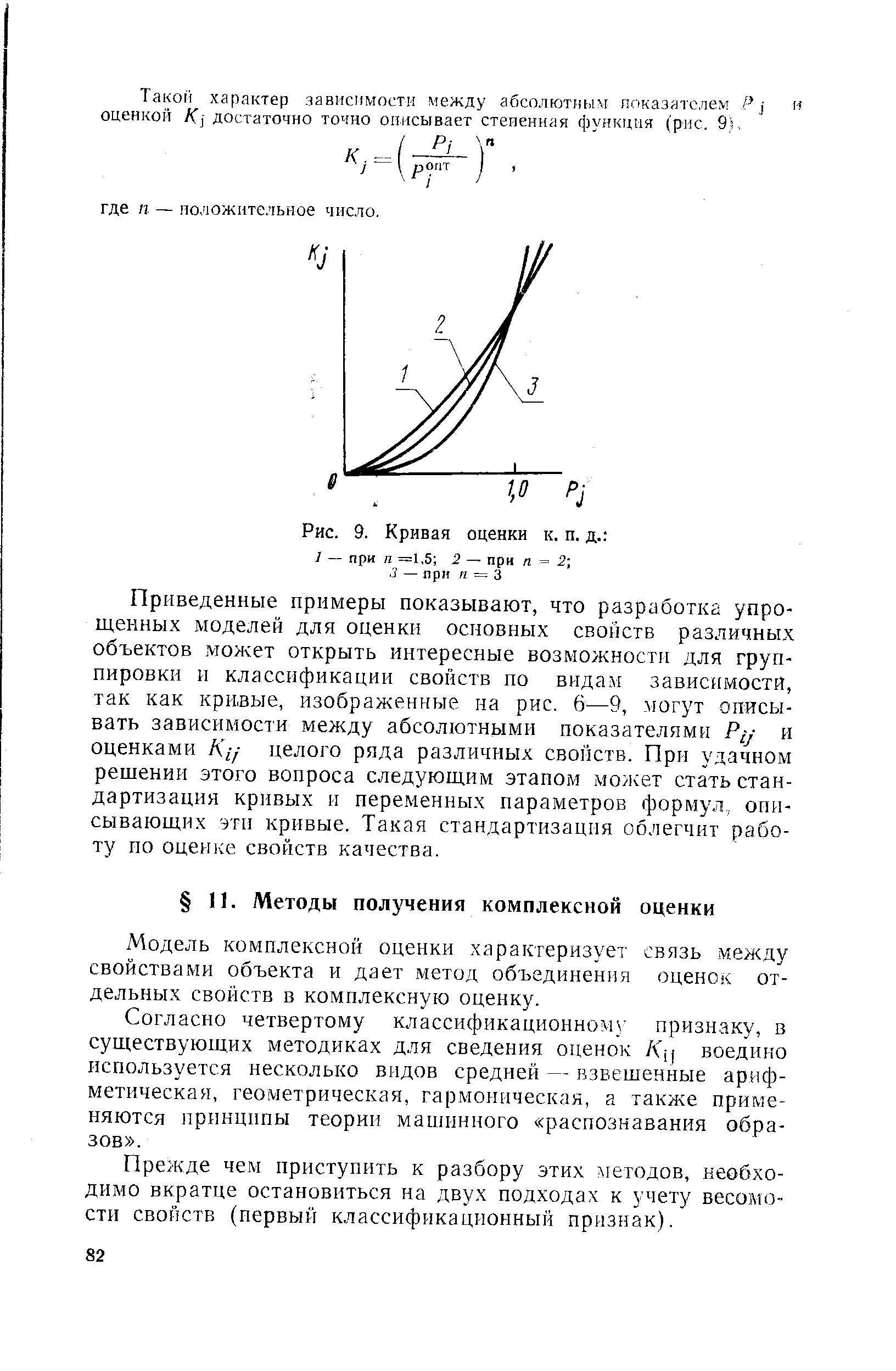
Методы получения комплексной оценки

из "О квалиметрии "

Модель комплексной оценки характеризует связь между свойствами объекта и дает метод объединения оценок отдельных свойств в комплексную оценку. [c.82]
Согласно четвертому классификационному признаку, в существующих методиках для сведения оценок Кц воедино используется несколько видов средней — взвешенные арифметическая, геометрическая, гармоническая, а также применяются принципы теории машинного распознавания образов . [c.82]
Прежде чем приступить к разбору этих методов, необходимо вкратце остановиться на двух подходах к учету весомости свойств (первый классификационный признак). [c.82]
Лишь небольшое число авторов определяет комплексные оценки качества без учета весомости отдельных свойств. Например, А. К. Белявский — автор одной из первых работ по оценке качества строительной продукции [34—278] предлагал оценивать проекты крупноблочных домов по 128 показателям (объемно-планировочным, комфортным, конструктивным, экономическим, производственным, архитектурным и т. д.). При этом он считал, что определить удельный вес среди других каждого из показателей невозможно, да и не нужно . [c.83]
В работе [203] комплексный показатель качества продукции Ко получается путем перемножения дифференциальных показателей свойств Кц без учета их весомости М . [c.83]
Некоторые исследователи, применяя эту формулу, все же учитывают весомость свойств, хотя в расчетной формуле это обстоятельство не находит прямого отражения. [c.83]
Федоров [200] предлагает классификацию показателей свойств, при которой показатели одного уровня равноценны по весомости, и, следовательно, значение их весомости можно не включать в расчетную формулу. [c.83]
В методике оценки качества бытовых магнитофонов [66] для получения комплексной оценки также используется среднеарифметическая. [c.84]
Что касается весомости свойств, то, как уже говорилось в начале параграфа, в этой формуле они равны между собой. Обосновывая правильность применения средней геометрической величины, М. В. Федоров приводит следующий довод средняя геометрическая обладает свойством обращать комплексную оценку качества в нуль, если оценка одного из показателей равна нулю. [c.85]
Нам представляется, что этот довод не является достаточно серьезным, так как существуют довольно элементарные математические приемы, позволяющие решать ту же задачу по обращению в нуль комплексного показателя качества KQ и при применении других средних величин, например, средней арифметической. Подробнее об этом будет сказано в 20. [c.85]
Поскольку оценки качества, основанные на средней арифметической и средней геометрической, получили наиболее широкое распространение, то прежде чем перейти к описанию других методов, подведем некоторые итоги. [c.86]
По Существу, простота вычисления средней арифметической и способность средней геометрической превращаться в нуль, если оценка одного из свойств равна нулю, — единственные аргументы в пользу их применения. Поэтому можно сказать, что выбор из семейства средних, в котором насчитывается 14 средневзвешенных величин [74], именно средней арифметической или средней геометрической до настоящего времени, к сожалению, еще не обосновывается достаточно убедительными аргументами. [c.86]
Нам представляется, что все сказанное в этой цитате всецело можно отнести к проблеме осреднения при вычислении комплексных оценок качества. [c.86]

Вернуться к основной статье