Сетевое планирование

из "Экономико-математические методы "

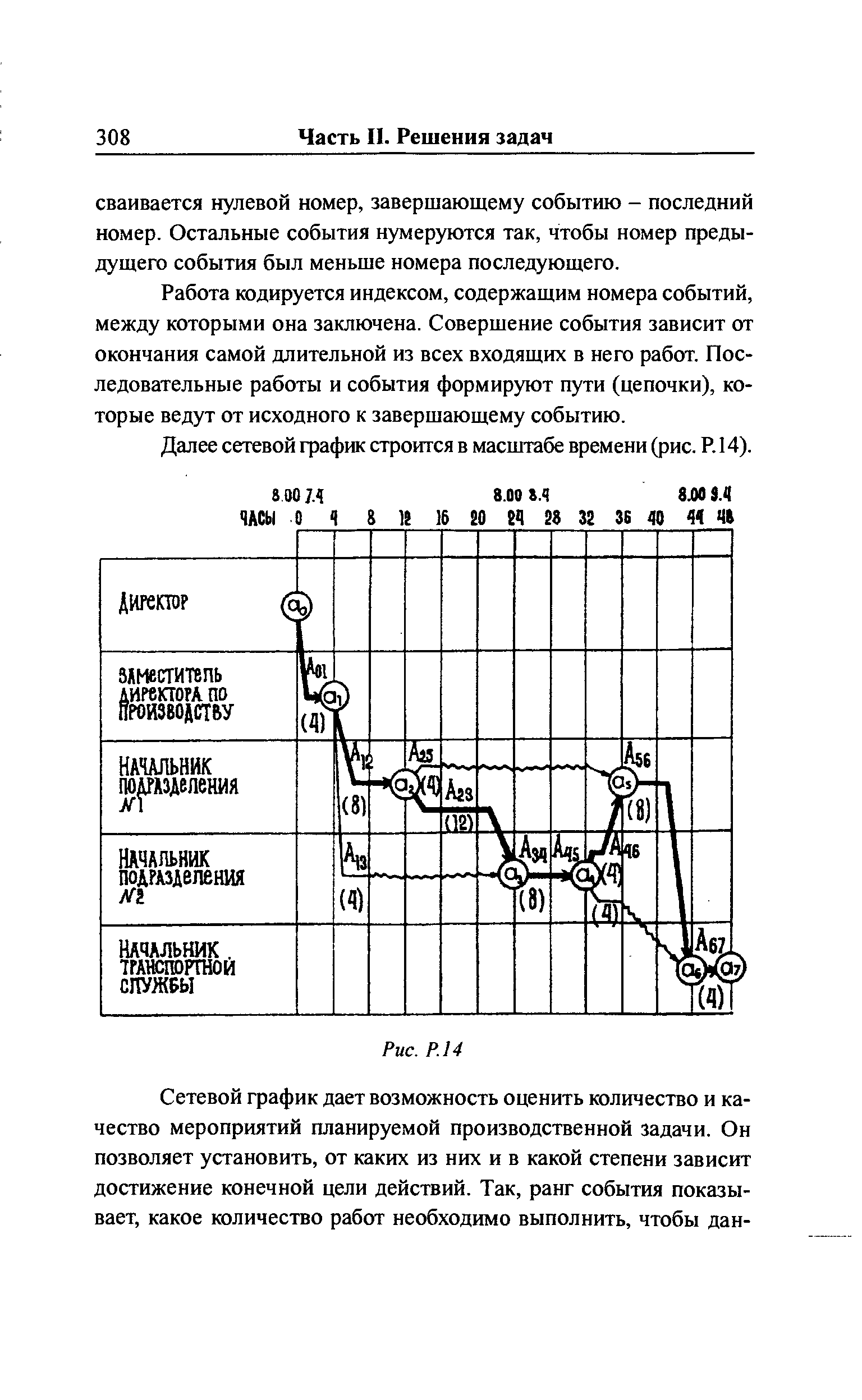
Работа кодируется индексом, содержащим номера событий, между которыми она заключена. Совершение события зависит от окончания самой длительной из всех входящих в него работ. Последовательные работы и события формируют пути (цепочки), которые ведут от исходного к завершающему событию. [c.308]
Далее сетевой график строится в масштабе времени (рис. Р. 14). [c.308]
После построения сетевого графика производится его анализ. Для этого строится так называемый критический путь. Это полный путь, на котором суммарная продолжительность работ является максимальной. Иными словами, это самый длинный по времени путь в сетевом графике от исходного до завершающего события. Критический путь лимитирует выполнение задачи в целом, поэтому любая задержка на работах критического пути увеличивает время всего процесса. На рис. Р. 14 критический путь обозначен жирной линией. [c.309]
Сущность анализа сетевого графика заключается в том, что выявляются резервы времени работ, лежащих вне критического пути, и направляются на работы, лежащие на критическом пути, который лимитирует срок завершения работы в целом. В нашем примере продолжительность работ, лежащих на критическом пути, равна 4 + 8+ 12 + 8 + 4 + 8 + 4 = 48 ч. Это и есть общее время решения всей производственной задачи. [c.309]
Аи в подразделении 1 на 8 часов, т.е. до 12 часов. При этом подразделение 2, лишенное части ресурсов, увеличит время своей работы на эти же 8 часов (работа А 3 станет равна 12 часам) и критический путь между событиями а и а2 будет равен 12 часам. Это сокращение общего времени критического пути означает и сокращение на то же время — на 8 часов - продолжительности решения всей производственной задачи. [c.310]
Руководствуясь данными табл. Р.5.6 и Р.5.7, строим сетевой график (рис. Р. 15 а). [c.310]
Выявляем критический путь, который показан на рисунке двойной линией. При этом длина критического пути, а значит, и общая продолжительность работ оказывается равной 5 часам. [c.310]
Анализ графика показывает, что существуют определенные резервы времени теща вместе с дочерью сделают уборку за 1 час и будут целых 3 часа ожидать без работы, пока жена купит продукты и приготовит ужин, чтобы можно было накрывать на стол. [c.311]
Вывод целесообразно перераспределить ресурсы, перебросив на критический путь дочь, освободив при этом ее от уборки квартиры. Тогда сетевой график приобретет вид, показанный на рис Р. 15 б, и общая продолжительность операции сократится с 5 до 3 часов. [c.311]

Вернуться к основной статье