Модели и алгоритмы интеллектуальных систем

из "Интеллектуальные системы "

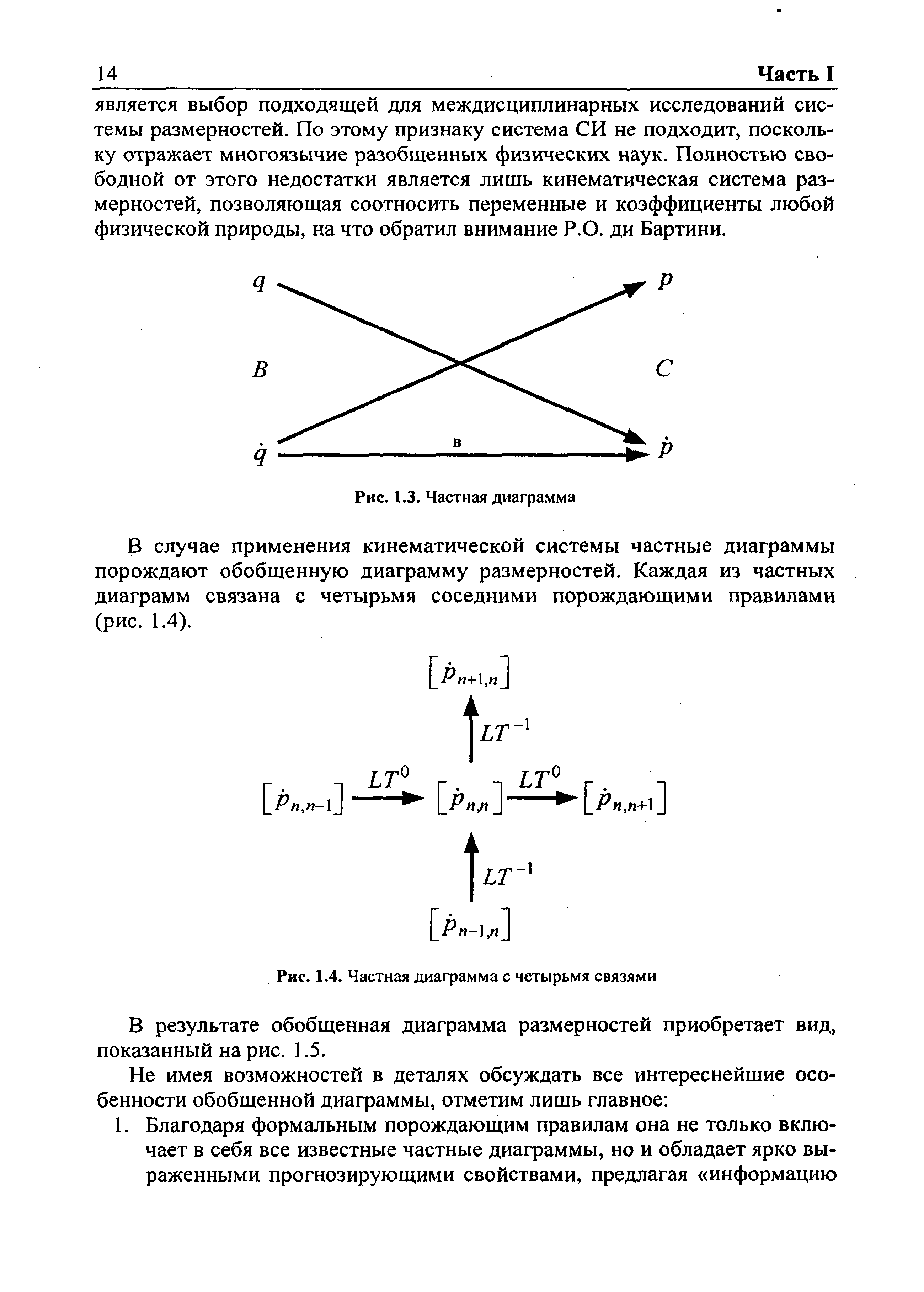
В результате обобщенная диаграмма размерностей приобретает вид, показанный на рис. 1.5. [c.14]
В соответствии с [3] ИС определены как некоторые объединённые единым информационным процессом системы, вырабатывающие на основе сведений и знаний при наличии мотивации (цели) решение о действии и реализующие его рациональным способом. В [4-6] рассматривались некоторые вопросы построения структуры ИС, отдельных элементов в составе ИС, а также алгоритмы функционирования последних и самих ИС. В перечисленных работах лишь частично затрагивались вопросы построения моделей ИС, что в первую очередь важно для решения на базе ИС различных задач управления теми или иными объектами, формирования алгоритмов обработки информации. Необходимость построения модели ИС (в том числе и математической) обусловлена невозможностью решения без её знания многочисленных задач в теории ИС. Отдельным вопросам, связанным с решением этой проблемы, посвящена данная работа, в которой также предлагается подход использования построенной модели к решению некоторых задач управления. [c.16]
С учетом [5] структурную схему ИС можно представить в виде, непосредственно используемом в задаче синтеза (см. рис. 1.7). [c.16]
Неконтролируемые составляющие z, управление и также удовлетворяют аналогичному соотношению, т.е. [c.19]
Определение 1.1. s -окрестностью множества Q в пространстве R 1 называется такое множество Q элементов р е R , что каждый элемент Р е Q удален от множества Q не более, чем на величину i в смысле некоторой меры близости ( ), определенной в R ]. [c.19]
Модель ИС можно считать построенной в том случае, если определены классы операторов, на которых следует выбирать оператор F интеллектуального преобразователя и оператор К выработки управления. [c.20]
Таким образом, соотношения (1.16)-(1.18) определяют вид оператора интеллектуального преобразования F. [c.22]
На основе уравнения состояния объекта (1.1) и полученных уравнений состояния ИП (1.17) или (1.18) можно сформировать математическую модель ИС. [c.24]
ИС с уравнением состояния (1.25) будем обозначать через I, а объект (1.1), для которого она построена, — через I. [c.24]
Рассмотрим возможный вид вектор-функций F2 ( ) или F(-) в уравнениях динамической модели состояния (1.17), (1.18), основываясь на концепции структурно-алгоритмического механизма функционирования ИС. В соответствии с данной концепцией алгоритм функционирования и структуры ИС определяется характером её взаимодействия с интеллектуальной средой, обозначаемой через S и представляющей собой некоторое непрерывное множество (пространство, многообразие), на элементах которого осуществляется анализ характера выполнения цели С, стоящей перед системой I, и формирование на основании этого решения, направленного на выполнение данной цели С. Для этого из пространства Н на среду S с помощью некоторого оператора Р осуществляется отображение (проектирование) системы I, цели С и модели окружающей среды 0, воздействующей на объект (1.1) посредством векторов возмущения ш (в рассматриваемом случае информация о 0 сводится к соотношению (1.4)). Об операторе Р будем использовать предположение, что в области его значений, т.е. на множестве 1тР с S, существует обратный оператор Р 1. [c.26]
В дальнейшем рассматривается именно этот случай. А уравнение (1.35) является уравнением состояния образа I v на элементах среды S. [c.27]
Для определения образа s необходимо воспользоваться соотношением (1.4), определяющем модель . Поскольку согласно (1.4) 0 не зависит от вектора X, а проектирование в среду S осуществляется в соответствии с (1.32), то модель 0 не изменяется в результате проектирования, и потому 0Л. = 0. [c.27]
Таким образом, формирование Y2(/) осуществляется на основе соотношений (1.35), (1.38), (1.45), (1.46) при произвольно выбираемых реализациях z°(-), o°(-) и значении s0 с учетом заданных ограничений (1.5), (1.4), (1.43). [c.29]
Таким образом, полученные соотношения раскрывают структурно-алгоритмический механизм функционирования ИП, в соответствии с которым выходной сигнал ИП формируется на основе соотношений (1.35), (1.38), (1.45), (1.46), когда используемая информация о z, оэ соответствует действительности. При этом в случае несоответствия действительности имеющейся информации и предотвращения возможности нарушения ограничения (1.37) используются соотношения (1.5 )-( .53), (1.56)-(1.60), позволяющие корректировать выходной сигнал ИП и формировать требуемый закон управления. [c.33]
В соответствии с предлагаемой моделью ИП, а также с учетом рассмотренной ранее модели БВУ сформулируем задачу построения управления объектом (1.1) в контуре ИС. Согласно механизму функционирования ИП задача построения разбивается на три, вообще говоря, самостоятельных задачи, каждая из которых представляет собой соответствующий этап решения общей задачи синтеза и решение которых необходимо осуществлять в последовательном порядке. [c.33]
Первая задача ставится с учетом априорной информации о возмущении со и неконтролируемой составляющей z, заданной соотношениями (1.4) и (1.5). Данная задача может рассматриваться как на элементах пространства состояний ИС Н, так и на элементах интеллектуальной среды S. Поскольку второй и третий этапы решения общей задачи синтеза предполагается осуществлять непосредственно на элементах среды S, то, без ограничения общности, и первую задачу будем рассматривать в рамках среды S. [c.33]

Вернуться к основной статье