Основные свойства выпуклых множеств

из "Приближенное решение задач оптимального управления "

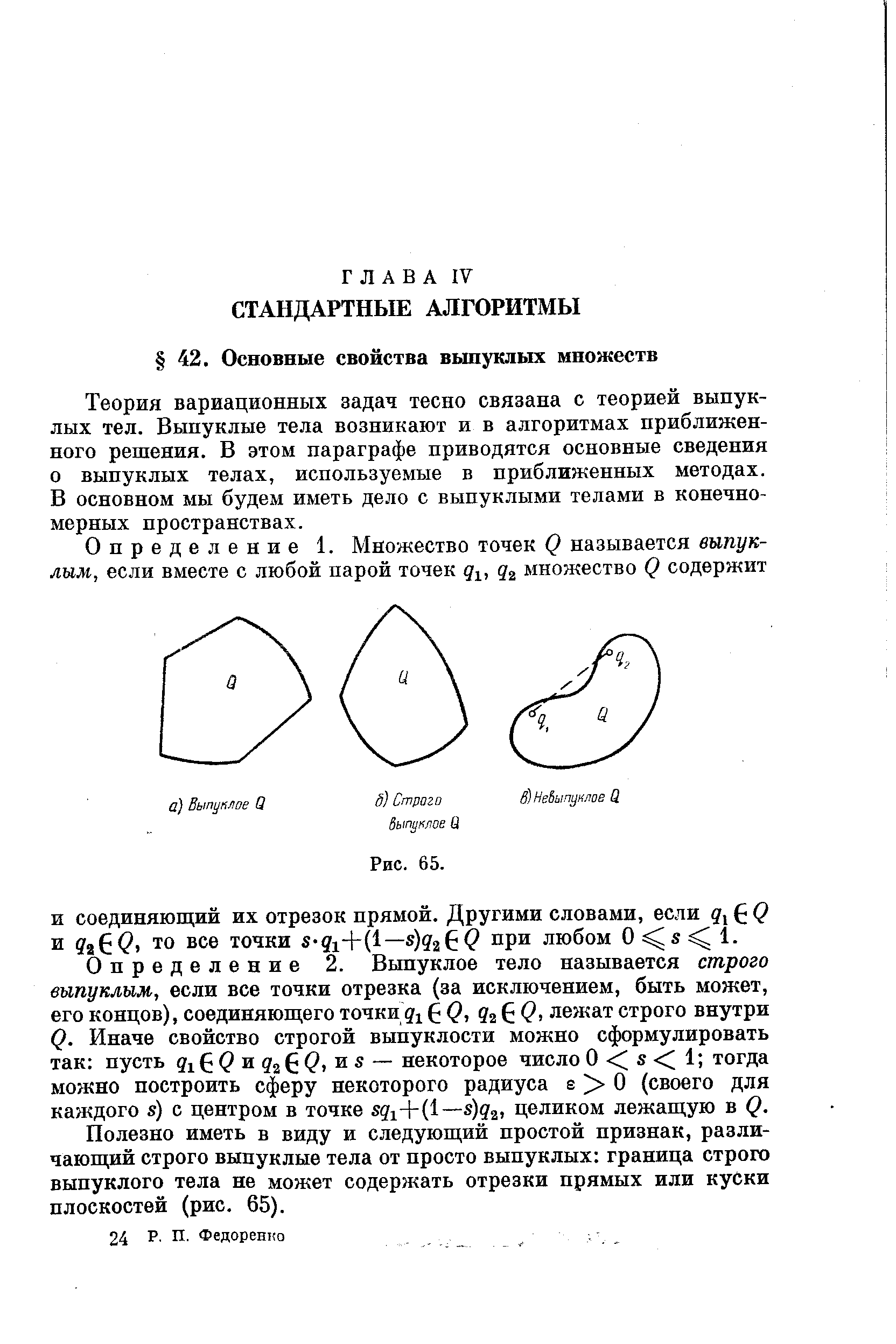
Теория вариационных задач тесно связана с теорией выпуклых тел. Выпуклые тела возникают и в алгоритмах приближенного решения. В этом параграфе приводятся основные сведения о выпуклых телах, используемые в приближенных методах. В основном мы будем иметь дело с выпуклыми телами в конечномерных пространствах. [c.369]
Полезно иметь в виду и следующий простой признак, различающий строго выпуклые тела от просто выпуклых граница строго выпуклого тела не может содержать отрезки прямых или куски плоскостей (рис. 65). [c.369]
Нас в основном будут интересовать замкнутые выпуклые тела. Границу такого тела Q будем обозначать dQ, причем 5Q Q в силу замкнутости. Важным для дальнейшего является следующий объект, обобщающий привычное понятие касательной плоскости. [c.370]
Очевидно, что все точки этого множества лежат в гиперплоскости G. [c.370]
Важным для дальнейшего является следующий простой факт. [c.370]
Следующая важная теорема об отделимости выпуклых тел существенно используется как в теоретическом анализе, так и в вычислениях. [c.371]
Замечание. Почти без всяких изменений проходит доказательство теоремы 2 в случае, когда одно из тел Q — неограничено. [c.371]
Предположение. Образ U в отображении F (и) есть строго выпуклое замкнутое ограниченное множество. [c.372]
В этом случае задача на условный экстремум (9) может быть сформулирована в виде следующей задачи строго выпуклого программирования в строго выпуклом ограниченном замкнутом множестве Q нужно найти точку вида е с наименьшим значением I (здесь е= 1, 0, 0,. . ., 0 ), т. е. [c.372]
по существу, задача на безусловный экстремум, так как условие нормировки (g, e) легко учитывается как при аналитическом решении этой задачи (если оно возможно), так и при численном методе подъема по градиенту. [c.373]
Лемма 2. max / (g) Л, м достигается этот максимум на векторе g, определяющем опорную к Q в точке Ле гиперплоскость. [c.374]
Однако рассматриваемый нами случай строго выпуклого программирования в этом отношении вполне благополучен функция R (g) дифференцируема. Более того, ее производная dR/dg вычисляется достаточно просто, и нет необходимости прибегать к численному дифференцированию. [c.376]
Доказательство. Проверим, что для любого вектора z lim Д( + 0-Д(У) =(g(g), z). (20). [c.376]
Для доказательства достаточно показать, что Пт 4 [(г.,. [c.376]

Вернуться к основной статье