Системы массового обслуживания

из "Основы имитационного моделирования сложных экономических систем "

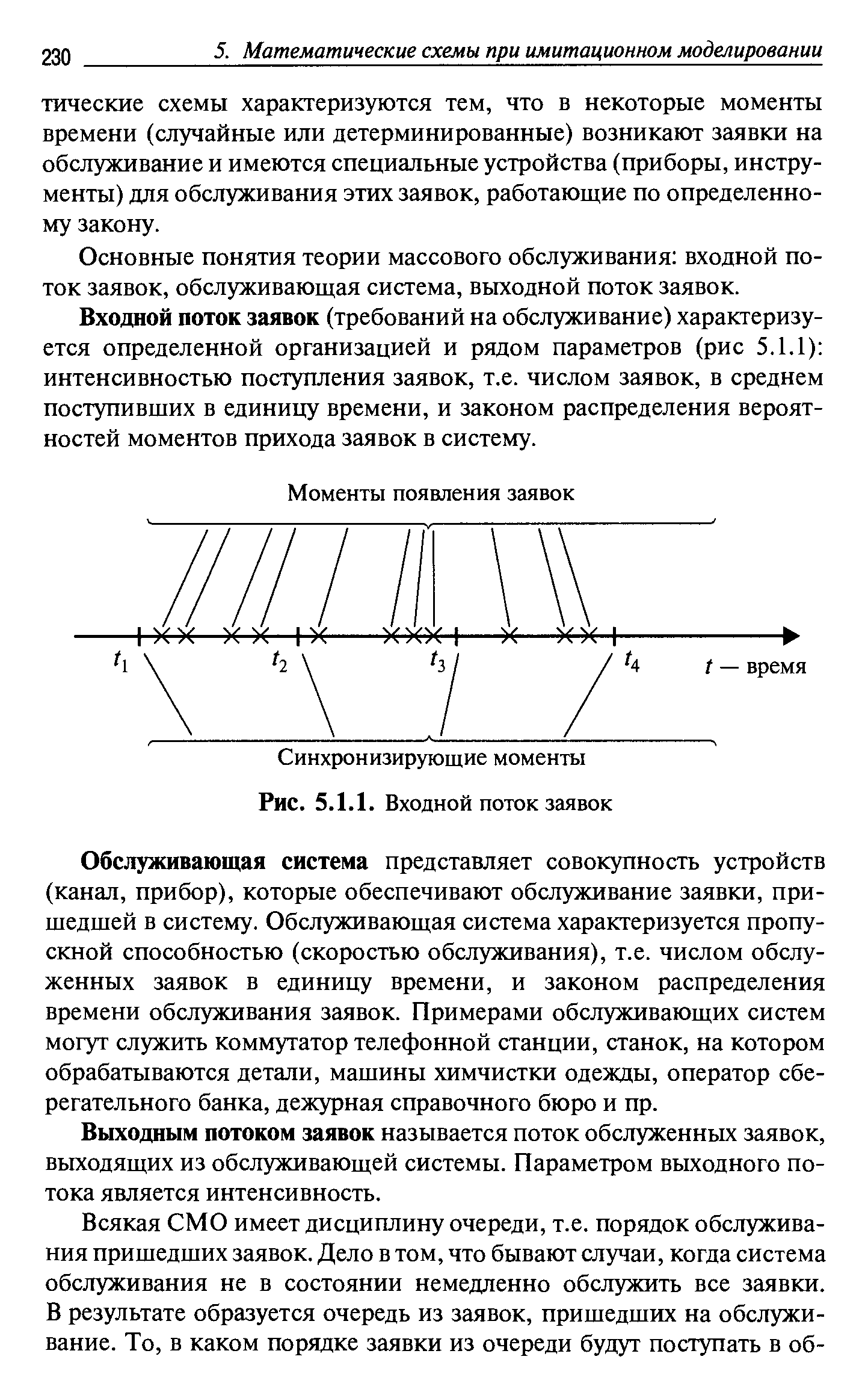
Основные понятия теории массового обслуживания входной поток заявок, обслуживающая система, выходной поток заявок. [c.230]
Входной поток заявок (требований на обслуживание) характеризуется определенной организацией и рядом параметров (рис 5.1.1) интенсивностью поступления заявок, т.е. числом заявок, в среднем поступивших в единицу времени, и законом распределения вероятностей моментов прихода заявок в систему. [c.230]
Обслуживающая система представляет совокупность устройств (канал, прибор), которые обеспечивают обслуживание заявки, пришедшей в систему. Обслуживающая система характеризуется пропускной способностью (скоростью обслуживания), т.е. числом обслуженных заявок в единицу времени, и законом распределения времени обслуживания заявок. Примерами обслуживающих систем могут служить коммутатор телефонной станции, станок, на котором обрабатываются детали, машины химчистки одежды, оператор сберегательного банка, дежурная справочного бюро и пр. [c.230]
Выходным потоком заявок называется поток обслуженных заявок, выходящих из обслуживающей системы. Параметром выходного потока является интенсивность. [c.230]
Рассмотрим более детально характеристики входного потока заявок и простейшие СМО. Потоком однородных событий называют временную последовательность появления заявок на обслуживание при условии, что все заявки равноправны. Существуют также потоки неоднородных событий, когда та или иная заявка обладает каким-то приоритетом. [c.231]
Если поток однородный, то каждое событие характеризуется только моментом его наступления tj. Существует два способа задания однородных событий. Первый способ заключается в перечислении всех известных моментов tj. Второй способ заключается в указании зависимости, позволяющей рассчитать tj по предыдущим значениям. [c.231]
Часто применяется случайный поток событий с ограниченным последействием, т.е. когда случайные величины ,у- независимы. [c.231]
Существуют также стационарные потоки, для которых вероятностный режим потока во времени остается неизменным. Это означает, что число заявок, поступивших в СМО в единицу времени, постоянно. [c.231]
Потоком с отсутствием последействия называется такой поток, у которого число заявок, поступивших в данный момент, не зависит от числа заявок, обслуженных в предыдущий момент. Поток с отсутствием последействия — частный случай потока с ограниченным последействием. Для потока без последействия вероятность Pk(t0, t) наступления k событий за интервал (t0, /0 + /) не зависит от возникновения событий до момента /0. [c.231]
Эта величина характеризует среднее число событий в единицу времени для данного потока. [c.232]
Такой поток часто используется в практических задачах, возникающих в экономических приложениях. [c.232]
Ординарным потоком называется такой поток, в котором невозможно появление двух и более событий одновременно. В практике часто приходится сталкиваться с групповыми заявками, т.е. несколькими событиями, появляющимися одновременно. Такие потоки не являются ординарными. [c.232]
Для расчетов параметров СМО на основе потока Пуассона необходимо проверить, соответствует ли он закону распределения Пуассона. Признак потока Пуассона — равенство математического ожидания X дисперсии G, т.е. X = и. [c.233]
Пусть х — число заявок, поступивших за единицу времени, т — число единиц времени, а п — общее число поступивших заявок. [c.233]
Пример. Проверить, является ли поток требований в систему распределенным по закону Пуассона. [c.233]
В связи с тем что х Сгх, поток можно считать пуассоновским. [c.234]
Простейший поток и поток с равномерным распределением интервалов времени между последовательными событиями наиболее часто применяются в теории и практике СМО. [c.234]
Поток событий называется регулярным, если длина интервала между событиями — постоянная величина. Примерами такого потока могут служить ежедневные сводки о каких-либо событиях (отчеты о дневной выручке в магазине, ежедневная сумма сделок на бирже или прихода средств в банк и т.п.), регламентированный поток деталей, сходящих с конвейера, поток поездов в метро и др. [c.234]
Потоки событий различного вида могут разрежаться и объединяться [37]. К сожалению, эти термины могут применяться только к потокам определенного вида. Так, например, если интервалы в потоке Эрланга п -го порядка уменьшить в (п + 1) раз, то интенсивность полученного потока станет равной интенсивности исходного пуассоновского потока, и с ростом п такой поток становится сколь угодно близким к регулярному с той же интенсивностью. Такие нормированные потоки Эрланга дают различные типы потоков с последействием, начиная от потоков без последействия ( п = 1) и кончая регулярными (п = °°). [c.234]

Вернуться к основной статье