ПОИСК
Это наилучшее средство для поиска информации на сайте
Задача о взаимных расчетах
из "Компьютерная бухгалтерия для всех "
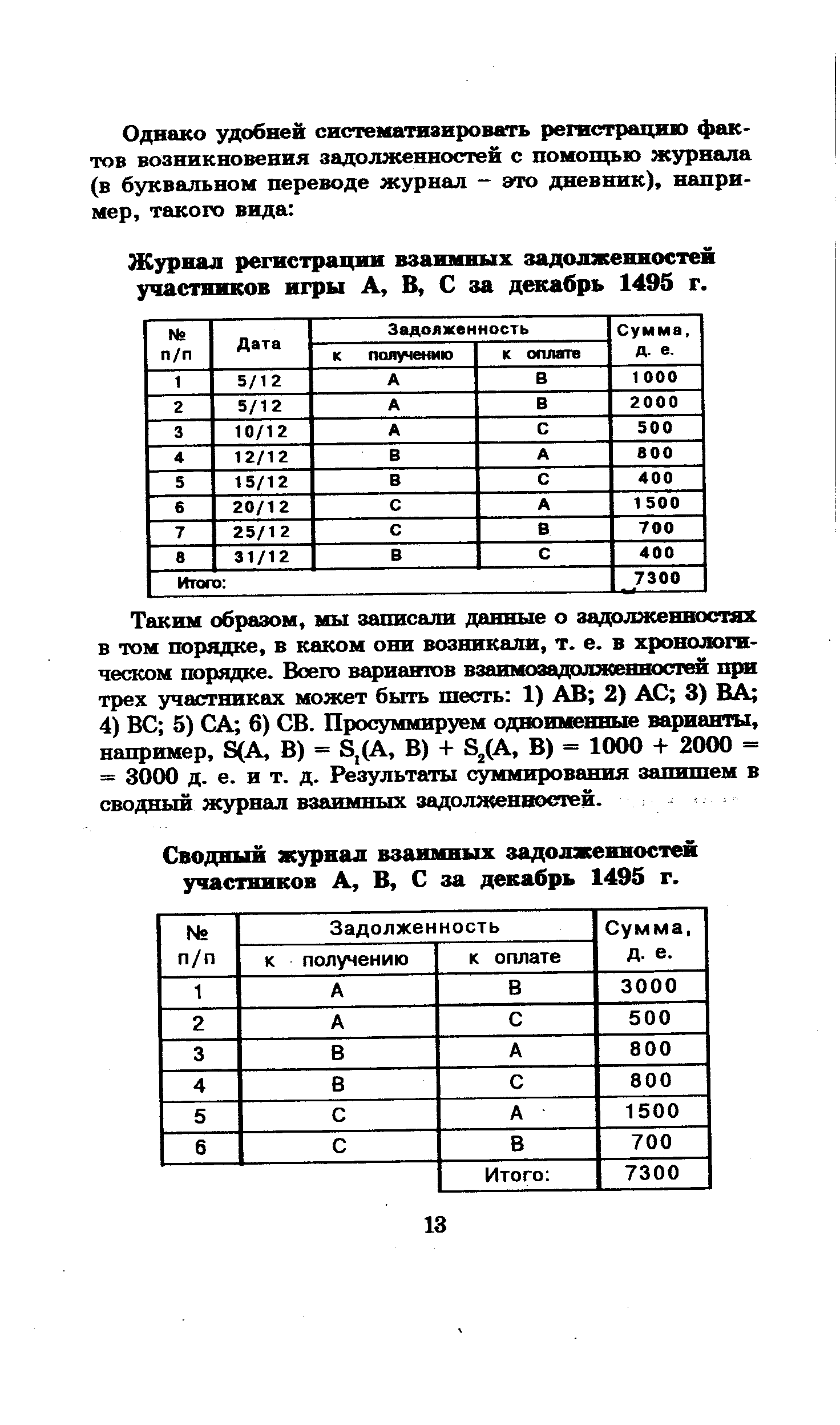
Журнал регистрации взаимных задолженностей участников игры А, В, С за декабрь 1495 г. [c.13]Сводный журнал взаимных задолженностей участников А, В, С за декабрь 1495 г. [c.13]
Задача заключается в том, чтобы к концу расчетного периода (в данном случае к концу месяца) произвести окончательные расчеты между участниками игры. Это можно сделать двояким образом а) произвести все шесть расчетов между участниками в соответствии с данными таблицы 2 по принципу Каждый сам за себя б) сделать необходимые расчеты и произвести взаимозачеты долгов. При втором варианте число платежей сократится ровно вдвое, соответственно для расчетов потребуется меньше наличных денег. [c.14]
Для того, чтобы произвести взаимозачет долгов между двумя любыми участниками X, Y = А, В, С необходимо из суммы к получению S(X, Y) вычесть соответствующую сумму оплаты S(Y, X), т. е. говоря бухгалтерским языком рассчитать сальдо (остаток) задолженности AS(X, Y) = S(X, Y) - S(Y, X). Если сальдо положительно AS(X, Y) 0, то оно (сальдо) и есть сумма к получению господином X от господина Y. И наоборот, если AS(X, Y) 0, то сальдо представляет собой сумму оплаты своего долга господином X господину Y. При этом запись AS(Y, X) = - AS(X, Y) О обозначает ту же сумму, которую господин Y должен получить от господина X. [c.14]
в нашем примере S(A, В) = 3000 — это есть сумма долга, которую А должен получить от В, a S(B, А) = 800 - соответственно, сумма к получению господином В от А. Сальдо AS(A, В) = S(A, В) - S(B, A) = = 3000 - 800 = + 2200 означает окончательную сумму долга, которую А должен получить от В при окончательном расчете. [c.14]
При расчетах между А и С соответственно получаем AS(A, С) - S(A, С) - S( , А) = 500 - 1500 = - 1000, а этот результат означает прямо противоположное - сумму к оплате задолженности господина А перед господином С или, что то же самое, AS( , А) = - AS(A, С) = + 1000 представляет собой сумму к получению господином С долга от господина А. [c.14]
Таким образом, при втором варианте расчетов необходимо произвести всего три платежа для погашения взаимных задолженностей между А, В и С, соответственно, для этого потребуется меньшая сумма наличных денег = 2200 + 1000 + 100 = 3300 д. е. (ср. с общей суммой 7300 д. е. при шести платежах по схеме Каждый сам за себя ). [c.15]
Шахматная таблица S взаимных задолженностей участников игры за декабрь 1495 т. [c.15]
Назовем эту таблицу для краткости таблицей выигрышей и обозначим ее буквой S, что понадобится нам при дальнейшем изложении. В математике таблицы чисел называются матрицами и над ними определены операции сложения, вычитания, умножения и транспонирования. Нам понадобятся только операции вычитания (сложения) и транспонирования матриц. [c.15]
Таким образом, транспонировать — это значит записать столбец таблицы S как соответствующую строку в таблицу S. В результате транспонированная к таблице S таблица S в нашем случае будет выглядеть следующим образом. [c.16]
Транспонированная шахматная таблица S взаимных задолженностей участников игры за декабрь 1495 г. [c.16]
Назовем, соответственно, транспонированную таблицу 8 таблицей или, что в нашем контексте то же самое, матрицей проигрышей. Если из матрицы выигрышей S вычесть матрицу проигрышей S, то получим таблицу сальдо окончательных расчетов как разность AS = S - S. [c.16]
Шахматная таблица AS сальдо окончательных расчетов участников игры на 31 декабря 1495 г. [c.16]
Матрица S(At) - это таблица, в которой записаны суммы выигрышей ( счета к получению ) за рассматриваемый период, а транспонированная к ней матрица S (At) это — таблица, в которой записаны просуммированные за тот же период суммы проигрышей ( счета к оплате ) тех же участников игры. [c.17]
Все матрицы AS(t), AS(t - 1), S(At), S (At) квадратные и одинакового размера, т. е. имеют одинаковое количество строк и столбцов, определяемое числом участников игры. В нашем примере размеры матриц имеют число строк 3 + 1=4, где + 1 - это итоговая строка, число столбцов также 3 + 1 = 4, где + 1 - это итоговый столбец. Таким образом, размер матрицы (3 + 1) х (3 + 1) или 4 х 4. В общем же случае, при числе участников игры М размеры матриц с итогами будут соответственно (М + 1) х (М + 1). [c.17]
Надо сказать, что в бухгалтерском учете такое представление информации не является традиционным. Обычно суммы к получению н суммы к оплате показывают с положительным знаком, но каждую. в своей колонке.. [c.18]
Вернуться к основной статье