Математическое приложение к главе

из "Финансовая математика Изд2 "

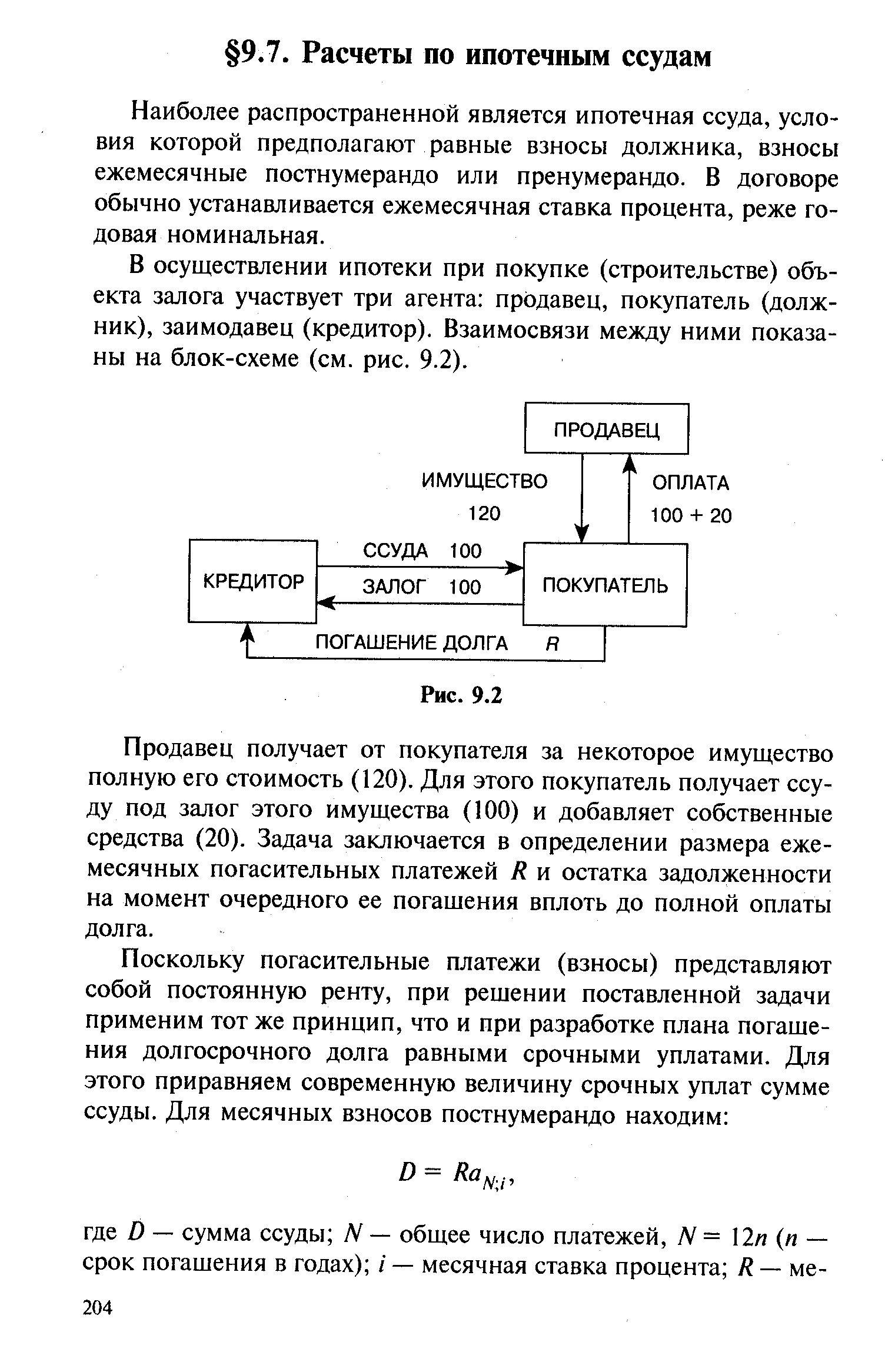
Наиболее распространенной является ипотечная ссуда, условия которой предполагают равные взносы должника, взносы ежемесячные постнумерандо или пренумерандо. В договоре обычно устанавливается ежемесячная ставка процента, реже годовая номинальная. [c.204]
В осуществлении ипотеки при покупке (строительстве) объекта залога участвует три агента продавец, покупатель (должник), заимодавец (кредитор). Взаимосвязи между ними показаны на блок-схеме (см. рис. 9.2). [c.204]
Продавец получает от покупателя за некоторое имущество полную его стоимость (120). Для этого покупатель получает ссуду под залог этого имущества (100) и добавляет собственные средства (20). Задача заключается в определении размера ежемесячных погасительных платежей R и остатка задолженности на момент очередного ее погашения вплоть до полной оплаты долга. [c.204]
Найденная по формуле (9.20) или (9.21) величина срочной уплаты является базой для разработки плана погашения долга. Согласно общепринятому правилу из этой суммы прежде всего выплачиваются проценты, а остаток идет на погашение долга. [c.205]
Как показано в таблице, в первом месяце расходы на выплату процентов и погашение основного долга соотносятся как 1000 434,71 в последнем месяце — уже как 14,21 1420,5. [c.206]
Далее расчет ведется по уже рассмотренной схеме. [c.207]
Ссуда с периодическим увеличением взносов. В этом варианте ипотеки задается последовательность размеров взносов. Пусть увеличение взносов происходит через равные интервалы времени т. В пределах каждого интервала взносы постоянны. Очевидно, что для полной сбалансированности схемы размер последнего взноса не задается, он определяется по сумме остатка задолженности. [c.207]

Вернуться к основной статье