Возможности применения моделей с переменными технологическими коэффициентами при решении задач планирования и управления комплексами непрерывного действия освещены также в работах [21—25]. В частности, в [22] рассматривается нелинейная задача статической оптимизации непрерывного производства. Предлагаются кусочно-линейная аппроксимация переменных коэффициентов и замена исходной нелинейной задачи некоторой приближенной задачей, для решения которой могут быть использованы методы линейного программирования. [c.16]
Кусочно-линейная аппроксимация 23 [c.471]
Машина МН-14 (рис. 3.3) является типичным образцом современной аналоговой вычислительной техники высокого класса. Состав математических блоков позволяет решать обыкновенные дифференциальные уравнения до 20-го порядка, а также широкий класс других задач, к числу которых можно отнести умножение переменной на постоянный коэффициент больше или меньше единицы суммирование переменных интегрирование по времени дифференцирование воспроизведение переменных коэффициентов методом кусочно-постоянной аппроксимации перемножение двух переменных умножение или деление шести. переменных на одну общую переменную воспроизведение нелинейных функций от одной переменной методом кусочно-линейной аппроксимации воспроизведение специальных нелинейных функций воспроизведение тригонометрических функций. [c.128]
Количество одновременно выполняемых операций колеблется в пределах от 120 (умножение переменной на постоянный коэффициент больше единицы) до 2 (воспроизведение специальных функций). Погрешность вычислений 0—0,8%. Максимальное значение погрешностей приходится на воспроизведение тригонометрических функций и на воспроизведение нелинейных функций методом кусочно-линейной аппроксимации (от 0,5 до 0,8%). [c.130]
Алгоритмы, использующие методы кусочно-линейной аппроксимации [c.69]
Для описания моделей используется различный математический аппарат методы субъективной вероятности, нечеткие множества, нейронные сети, кусочно-линейная аппроксимация, системы алгебраических и дифференциальных уравнений и т.д. Подобные модели являются средством уменьшения степени неопределенности при выборе возможных вариантов решений, генерируемых вычислительной системой. В качестве примеров, конечно, далеко не полных, рассмотрим неопределенность и связанную с ней субъективность, характерную для некоторых математических моделей. [c.88]
Для описания таких моделей используется различный математический аппарат методы субъективной вероятности, нечеткие множества, нейронные сети, кусочно-линейная аппроксимация, марковские случайные процессы, методы математического программирования и [c.168]
Согласование решений с помощью многокритериальных оценок. Наиболее известными среди них являются методы идеальной точки ранжирование по Парето функции (отношения) предпочтения ЛПР - согласование весов критериев и характеристик базовых шкал нахождением их центра тяжести кусочно-линейная аппроксимация функций предпочтения ЛПР метод X - коэффициентов. Подробно они рассмотрены в [5.8]. [c.169]
| Рис. 2.19. Варианты кусочно-линейной аппроксимации функции принадлежности | 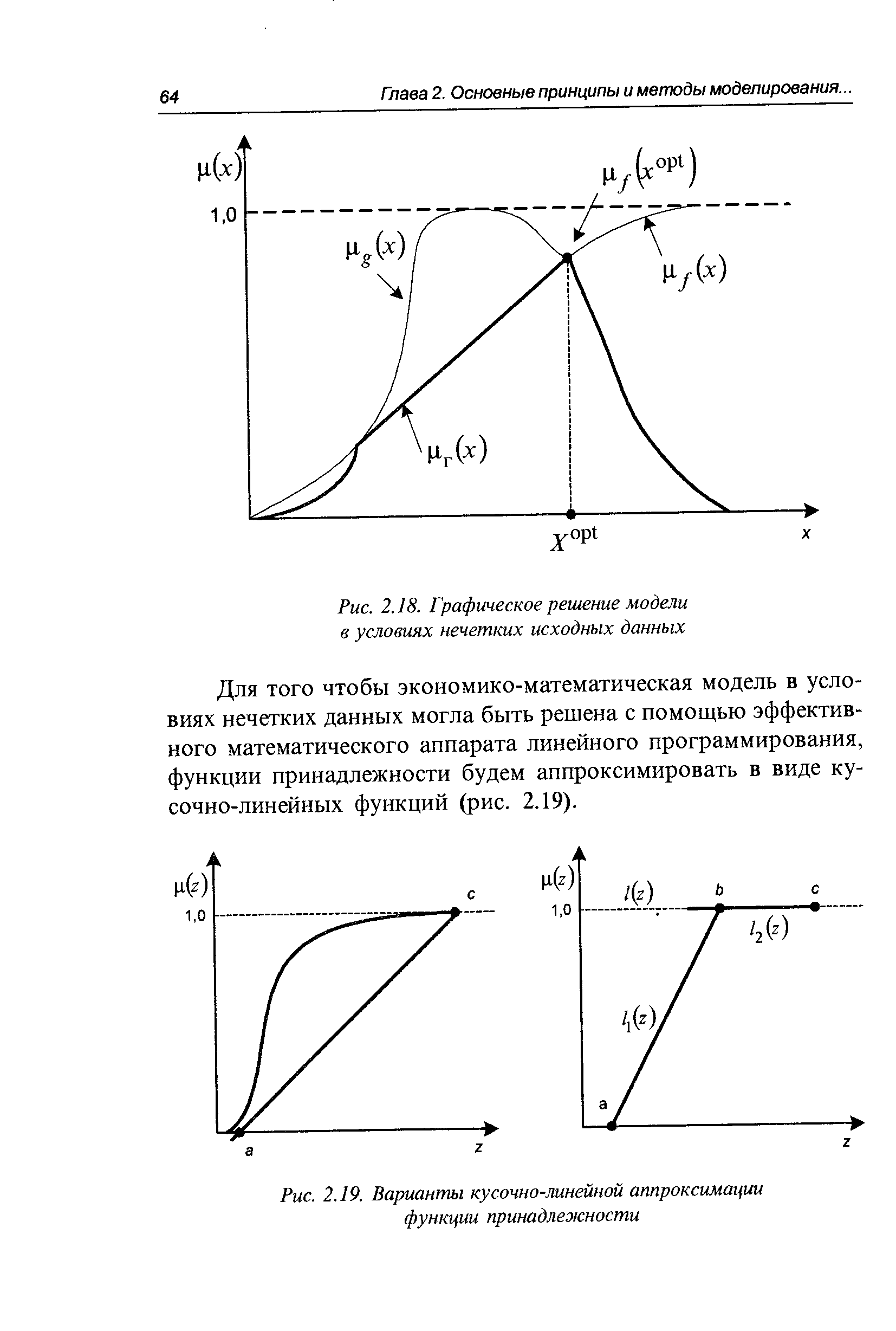 |
Особо следует отметить, что эта постановка может быть использована для построения кусочно-линейных аппроксимаций сложных зависимостей. [c.62]
Особо следует отметить, что этот же метод может быть использован для построения кусочно-линейных аппроксимаций сложных зависимостей, в этом случае а, -линейная модель в i -м классе, а К(х,а,) - отклонение значения выходного параметра у в данной точке х от модельного значения [5], т.е. функционал (4) имеет вид [c.64]
Предложенные методы обеспечивают генерацию огромного количества вариантов выполнения бизнес-процесса. При принятии решения по выбору одного или нескольких вариантов перед лицом, принимающим решения (ЛПР), стоят задачи оценки значимости отдельных составляющих ситуации и всей ситуации в целом анализа возможных решений, оценки их эффективности и последствий выбора решения, наилучшего с точки зрения ЛПР. Для их решения существует большое количество методов, основанных на формировании набора критериев и оценки их важности (метод анализа иерархий, метод нечетких множеств, метод Парето, метод кусочно-линейной аппроксимации и др.), методология предполагает применение любой их комбинации. [c.232]
Точное значение" F0=l приближенный метод дал решение с F0 d,025. Ошибка в 2,5% состоит из двух частей. Первая часть — это ошибка аппроксимации, возникшая из-за сужения задачи на класс кусочно линейных функций х (t). Эта ошибка имеет порядок шага т сетки tn и может быть вычислена по указанному выше точному решению задачи в классе кусочно линейных х (t). При шаге сетки t=0,02 точное сеточное решение дает F0=l,0130 (для напрашивающейся аппроксимации F0=1,0133). [c.293]
| Рис. 6.13. Истинная кусочно-линейная регрессия (—) и ее полиномиальная аппроксимация, полученная с помощью алгоритма структурной минимизации критерия адекватности | 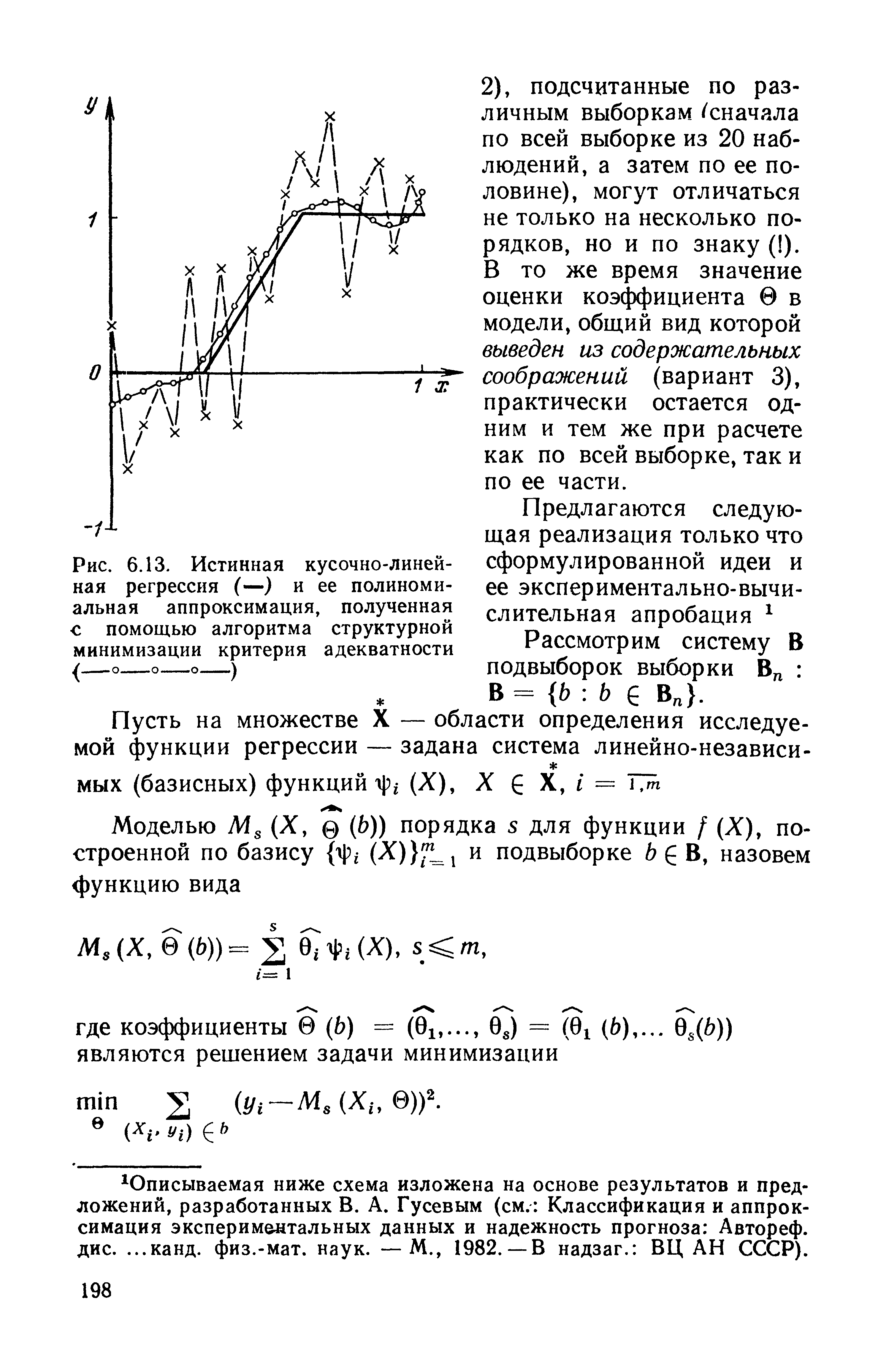 |
Функционал F0 [и ( )] вычислялся точным интегрированием в классе кусочно линейных функций х (t) интегрирование уравнения —ф=2я (t) также было точным в классе кусочнолинейных х (f). Эти предосторожности были связаны с наличием особенностей в искомом решении использование более простых аппроксимаций, которые были бы вполне приемлемы на гладких траекториях и ( ), ( ) , в данном случае приводит к заметным -ошибкам (см. в связи с этим также стр. 224). [c.290]
Напрашивающаяся аппроксимация очевидного точного решения кусочно линейной функцией с значениями х0=х1=.. . == =Ztf i=0, Xjv=l — неоптимальна. Оптимальная функция определяется решением разностного уравнения (аналог уравнения Эйлера) ) [c.292]
Ступенчатая аппроксимация fg(x) плотности fe(x) соответствует кусочно-линейной функции. Если абсциссы х , х2, ...хк скачков функции fg(x) суть квантили x0,xl,x2,...xR l [c.58]
