Используя данные примера 1, рассмотрим геометрическое решение задачи линейного программирования. Это позволит понять использование метода линейного программирования. [c.215]
| Рис. 8.4. Геометрическое решение задачи линейного программирования | 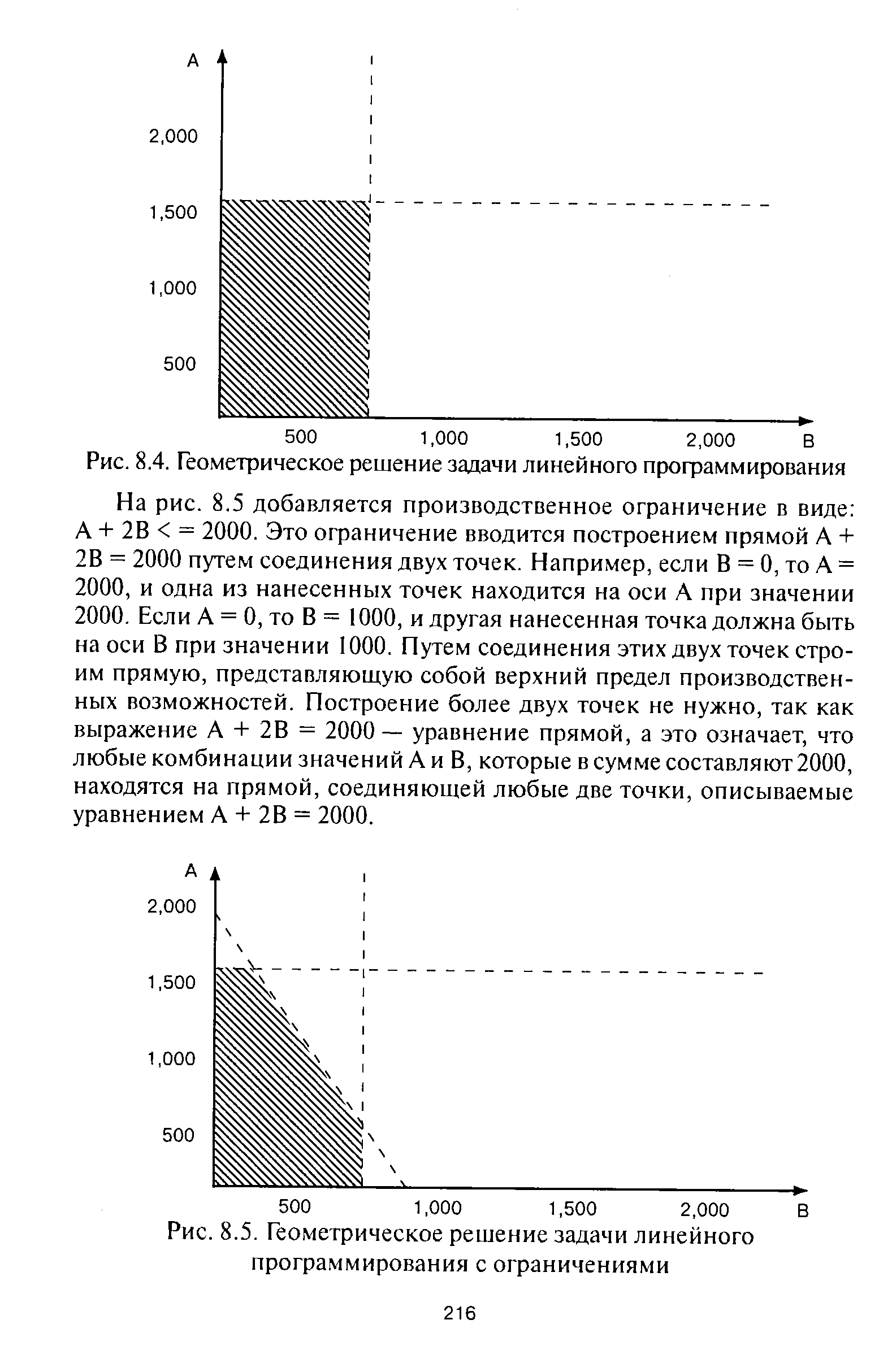 |
| Рис. 8.5. Геометрическое решение задачи линейного программирования с ограничениями | 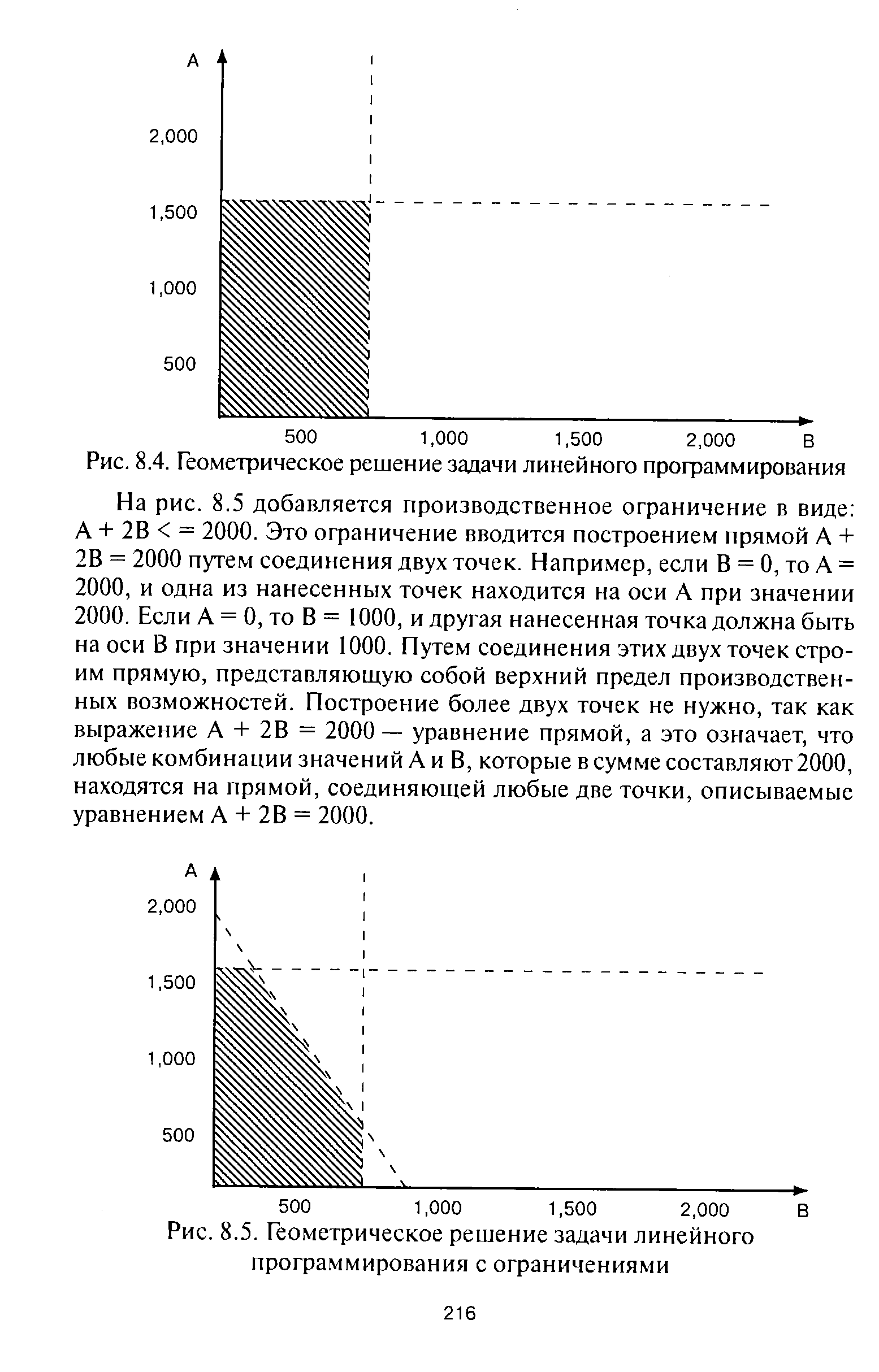 |
Рассмотренная геометрическая интерпретация задачи линейного программирования возможна лишь при наличии двух независимых переменных. При трех переменных наглядное представление существенно усложняется, так как в этом случае имеет место некоторый выпуклый многогранник в трехмерном пространстве, соответствующий объему допустимых планов. [c.65]
Симплекс-метод является алгебраической формой решения задачи линейного программирования, вытекающей из только что рассмотренного геометрического представления. При обосновании симплекс-метода будем прибегать к уже рассмотренному выше двухмерному случаю, что позволит достаточно просто перейти от геометрического представления к его алгебраической аналогии. [c.65]
Критерии непротиворечивости. Здесь будут даны три критерия непротиворечивости конечного набора векторов. Один из них имеет геометрическую форму, второй представляет собой алгебраический вариант, а третий — алгоритмический, удобный для реализации в среде программирования. [c.113]
Выпуклые многогранники и выпуклые многогранные конусы принадлежат к числу наиболее распространенных понятий математической экономики. В линейном и выпуклом программировании используются обязательно выпуклые области изменения переменных (допустимые множества по теоретико-множественной терминологии, многогранники — по геометрической) и выпуклые целевые функции. [c.57]
Многогранные К. используются при геометрической интерпретации процессов экономического роста, прогнозировании, в задачах линейного программирования. [c.153]
Понятие М. используется в геометрической интерпретации задач линейного программирования множество допустимых решений задачи является выпуклым М., базисное решение или опорный план — одной из его вершин. (См. Вершина допустимого многогранника). [c.198]
Теперь остался вопрос об алгоритме решения задачи (11)—(13). На первый взгляд и здесь нет никаких проблем, такой алгоритм, притом сходящийся со скоростью геометрической прогрессии, в сущности, давно известен. Это — алгоритм решения задачи строго выпуклого программирования (см. 42). Основанием для его применения служит [c.144]
Именно по этой причине автор предпочел конструкцию вариации управления типа (14). Требуя для своего формирования решения некоторых геометрических задач, она приводит к задаче линейного программирования, вертикальный размер которой равен числу входящих в задачу функционалов Ft [ ( )] [c.173]
Простые геометрические ограничения и (t) U превращаются в ограничения в фазовом пространстве, т. е. в ограничения в терминах функционала типа (1) они учитываются так, как это было описано выше, что увеличивает размерность задачи линейного программирования (15, 19). Правда, соответствующие элементы h n матрицы этой задачи вычисляются просто А = ( я—tn ) левее соответствующей точки аппроксимации, / =0 — правее ее. В целом замена (15) оказывается оправданной и позволяет эффективно решать прикладные задачи с хорошей точностью. [c.185]
Эксперимент. Были проведены расчеты с целью выяснить роль того основного элемента, который отличает используемый в расчетах алгоритм решения задачи квадратичного программирования от классического алгоритма строго выпуклого программирования. Речь идет о промежуточной минимизации x (см. 49). Для этого был проведен расчет по той же самой программе и в тех же условиях, что и расчет 4, с единственным изменением в программе решения задачи квадратичного программирования был отключен блок минимизации x , т. е. эта задача решалась стандартным процессом строго выпуклого программирования, сходящимся, как известно, со скоростью геометрической прогрессии. Результат оказался следующим затратив в 1,5 раза больше времени, чем этого потребовал весь расчет 4, удалось выполнить всего 6 итераций. К тому же эти 6 итераций относятся к самому легкому этапу решения задачи варьируется взятая произвольно управляющая функция и ( )=0,1, дополнительные условия F0 а и х1 (T)=R3 грубо нарушены задача квадратичного программирования не имеет решения и при использовании алгоритма 49 это быстро выясняется. Кроме [c.328]
Двойственный симплекс-метод. Начнем с анализа геометрической картины, связанной с задачей линейного программирования. На рис. 76 изображен (качественно) многогранник Р, причем одна ось — прямая е, в качестве второй оси на рис. 76 принято иг-мерное пространство. Граница Р состоит из т мерных граней (на рис. 76 они изображены отрезками). Каждая грань определяется вектором g, ортогональным данной грани. Мы будем считать этот вектор нормированным условием (g, е) = 1. Такие векторы определяют нижние грани Р, при нормировке (g, e) =—1 получим верхние. Это следует понимать так коль скоро задан вектор g, соответствующая ему грань определяется как совокупность точек х вида [c.426]
Система (7.28 ) решается итеративно, при этом веса оцениваются на основе параметров, полученных на предыдущем шаге. В качестве нулевого приближения параметров можно взять обычные мнк-оценки. Чтобы не иметь дела со слишком большими весами, выбирают какую-либо большую константу с >0 и для Wi с полагают wt = с. Для минимизации Ql (в) пользуются также методами линейного программирования [253, 2561 или специальным геометрическим приемом [53]. [c.214]
Смоляк С. А. Оптимальное восстановление функций и связанные с ним геометрические характеристики множеств. — В кн. Тр. 3 зимней школы по математическому программированию и смежным вопросам. — М. ЦЭМИ АН СССР, 1970, вып. 3, с. 509 — 557. [c.465]
Свое наименование С. м. л. п. получил из математич. понятия симплекс , обозначающего простейший выпуклый многогранник в пространстве с числом измерений, равным п (напр., при п=2 симплекс представлен многогранником на плоскости, при га=3 — тетраэдром и т. д.). Связь С. м. л. п. с математич. понятием симплекса заключается в том, что этот метод основан на замене перебора множества возможных значений переменных, геометрически представимых как точки такого многогранника, перебором одних только угловых точек, лежащих на границах соответствующего симплекса, в к-рых только и могут находиться отыскиваемые в рассматриваемых задачах экстремальные значения переменных. Такая замена дает огромную экономию в расчетах, что, собственно, и выводит задачи линейного программирования в число решаемых задач. [c.21]
Процедура С. м. л. п. не поддается элементарному изложению ввиду громоздкости ее расчетного алгоритма. Но общая идея, или логическая схема этого метода может быть разъяснена на основе изложенного выше геометрического представления о сущности задач линейного программирования. Эта идея заключается в том, что задача решается путем многошаговой расчетной процедуры. Значения отдельных переменных (неизвестных) вводятся в решение постепенно одно за другим т. о., чтобы не были нарушены поставленные ограничения и чтобы величина целевой функции на каждом шаге увеличивалась. Расчетная процедура начинается с такого положения, когда величина целевой функции равна нулю напр., при решении производств, задачи, подобной описанной выше, в качестве исходного положения принимается такое, когда выпуск отсутствует и все производств, мощности остаются неиспользованными. Далее, на следующем шаге расчета, в решение вводится одна переменная с таким значением, при к-ром не нарушается условие допустимости, т. е. не нарушаются поставленные ограничения. Подсчитывается, какие мощности остаются неиспользованными после этого, и переходят к следующему шагу. Разработана система признаков-показателей, сигнализирующих на каждом шаге о наличии резервов дальнейшего улучшения результатов или о достижении оптимума, а также о том, какие переменные надо ввести в решение и какие вывести из него для улучшения результата. Система вычислительных операций, основанных на указанных показателях, и составляет расчетный алгоритм С. м. л. п. [c.22]
Инстинкты — это акты поведения, связанные с удовлетворением биологических потребностей. Они генетически запрограммированы в половой клетке и передаются от поколения к поколению в стабилизовавшемся структурном отношении. Эти отношения определяют характерный для особей образ жизни. Например, пчелы и осы создают соты, для изготовления которых человеку необходимо решать задачу оптимального программирования, чтобы минимизировать затраты сырья для достижения оптимального результата вместимости. Они же затрачивают минимум вещества для создания максимального вместилища, четко соблюдая при этом геометрические пропорции ячеек. [c.9]
Математическое программирование — раздел математики. Он изучает методы решения задач на нахождение экстремума функций (показателя качества решения) при ограничениях в форме уравнений и неравенств. Объединяет разные математические методы и дисциплины исследования операций программирование, которое подразделяется на линейное и нелинейное, динамическое и выпуклое, геометрическое и целочисленное и др. [c.510]
Для практического решения задачи линейного программирования (7.34) - (7.36) на основе ее геометрической интерпретации необходимо следующее. [c.204]
| Рис. 7.5. Решение задачи линейного программирования геометрическим способом | 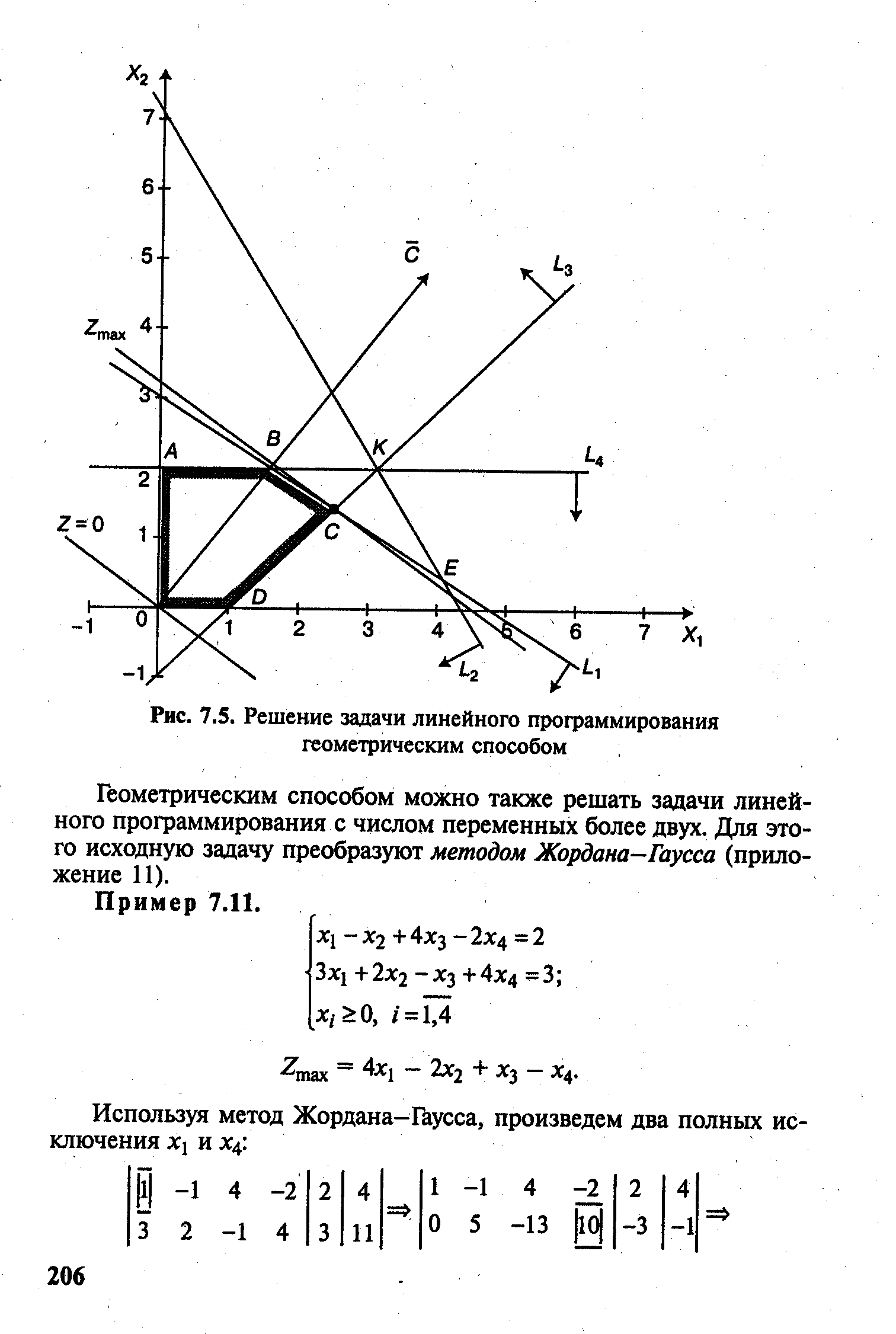 |
Рие. 7.6. Геометрическая интерпретация решения задачи линейного программирования [c.207]
| Рис. 7.7. Геометрическая интерпретация решения задачи линейного программирования (изменение ресурса А) | 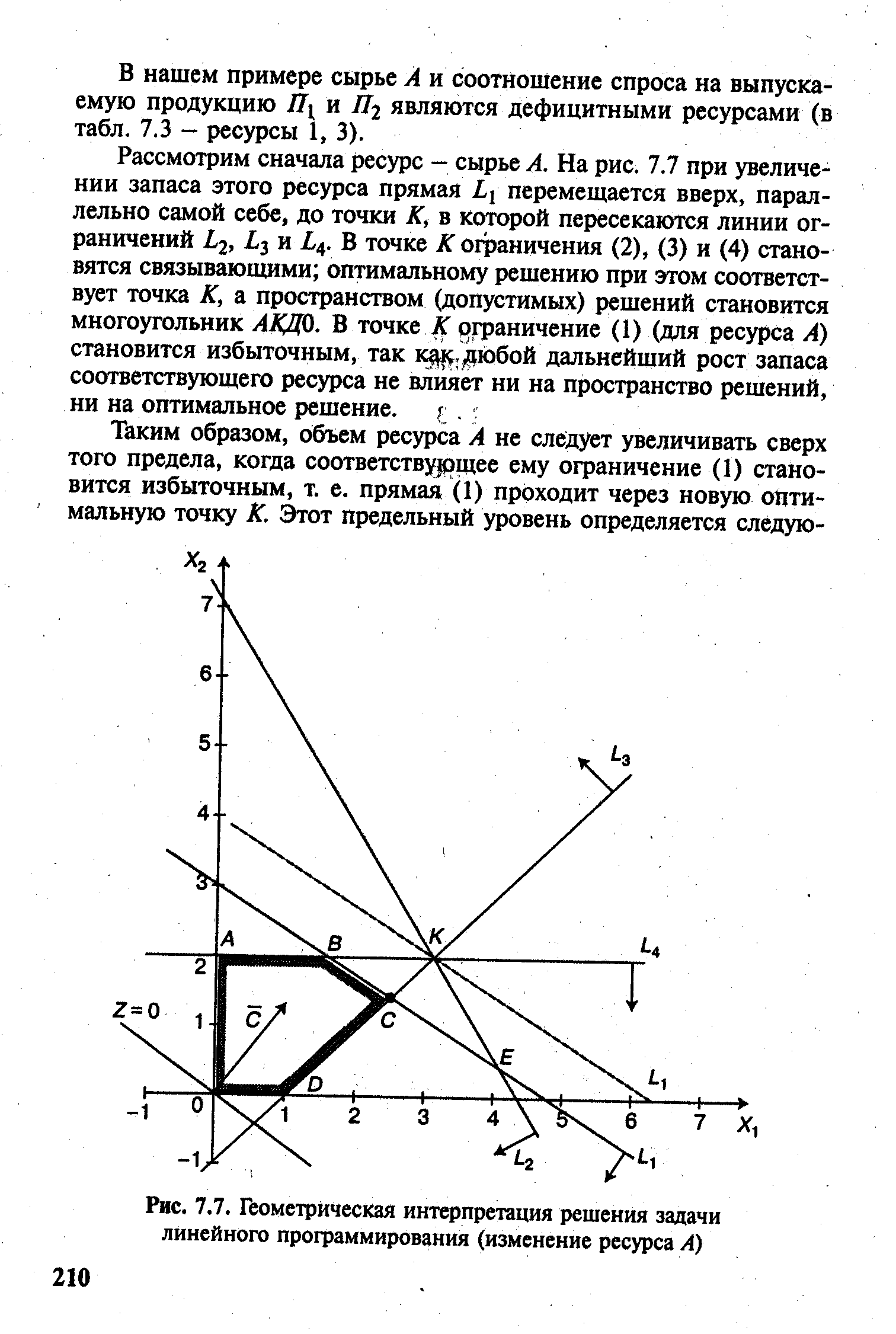 |
| Рис. 7.8. Геометрическая интерпретация решения задачи линейного программирования (изменение спроса на продукцию) | 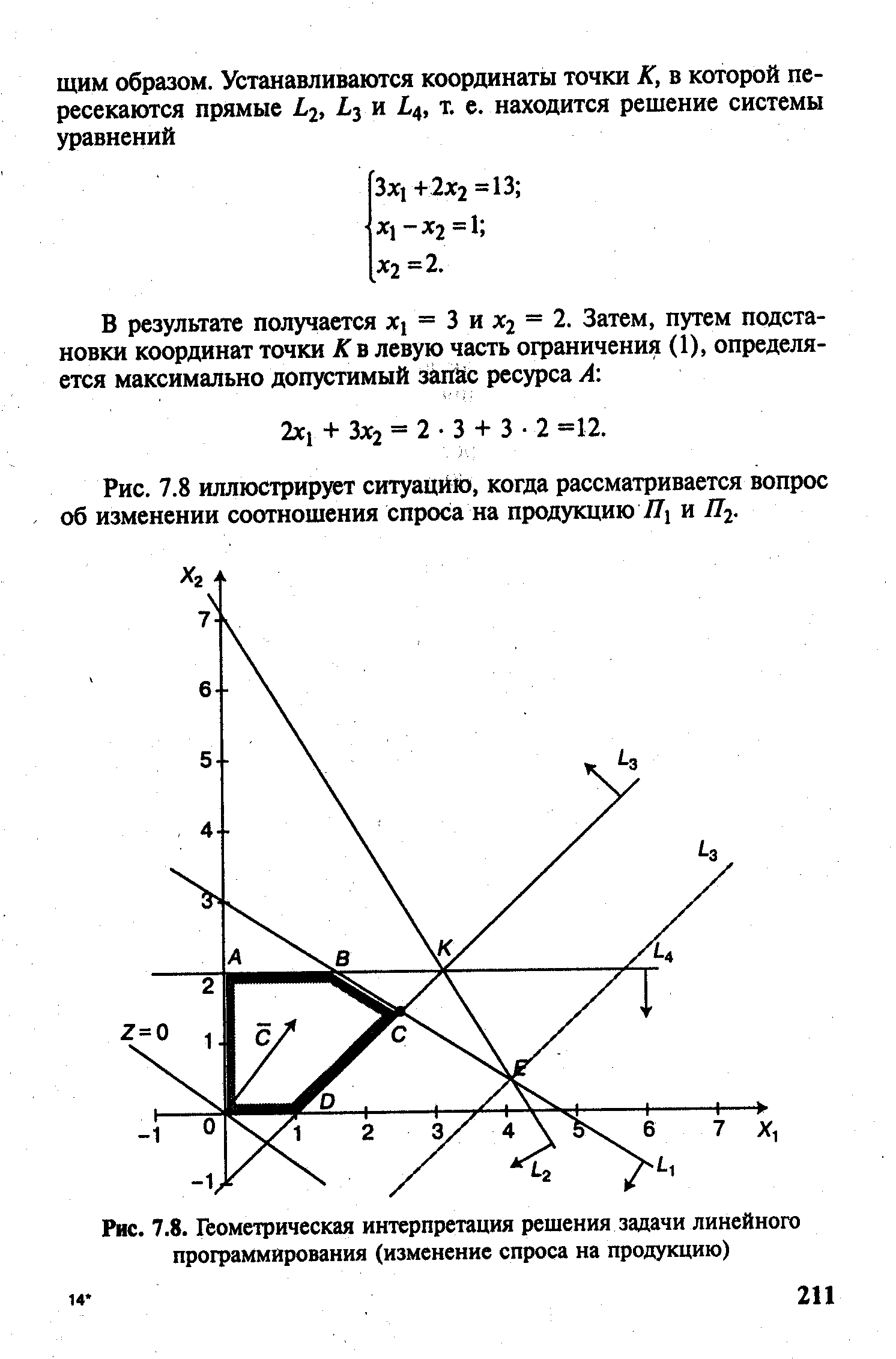 |
Проведем геометрическую интерпретацию задачи параметрического программирования. Полагая t = а и ограничиваясь только двумя переменными, получаем обычную задачу линейного программирования (рис. 12.1). [c.376]
При / = ос изменяются коэффициенты целевой функции, геометрически это значит, что прямая, соответствующая Za, повернулась на некоторый угол. Из рис. 12.1 следует, что Za max достигается в точке AI, a Za max - в точке А2. Естественно предположить, что при некотором значении t максимальное значение достигается одновременно в точках А1 и А2. В этом случае прямая, соответствующая целевой функции, параллельна стороне А А2 многоугольника решений. Фиксированное значение t является граничной точкой между двумя соседними интервалами отрезка [а, Р]. Исходя из изложенного, задачу параметрического программирования с двумя переменными можно решить графически. [c.376]
| Рис. 12.2. Геометрическое решение задачи параметрического программирования | 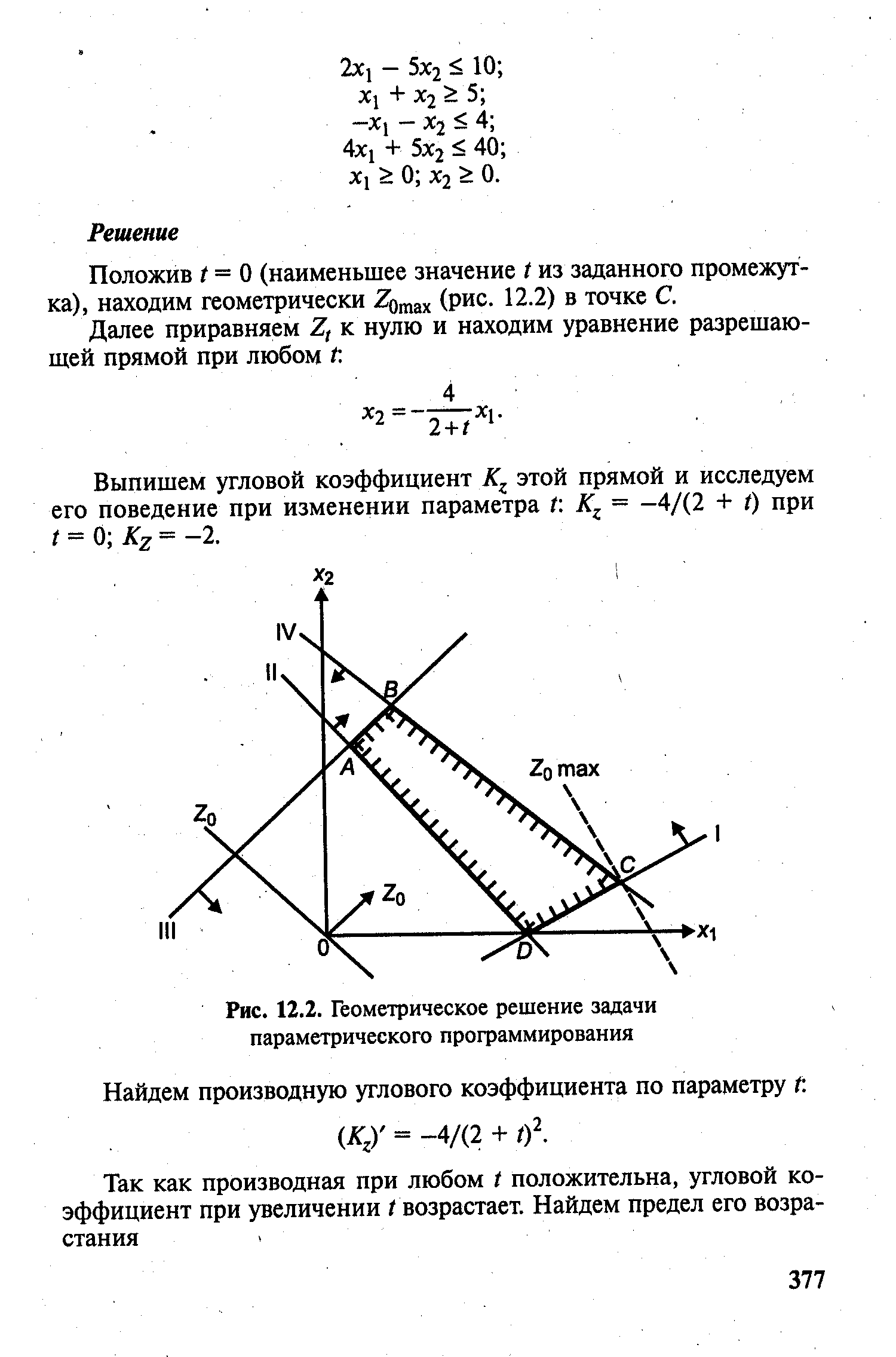 |
| Рис. 13.1. Геометрическая интерпретация решения задачи целочисленного программирования | 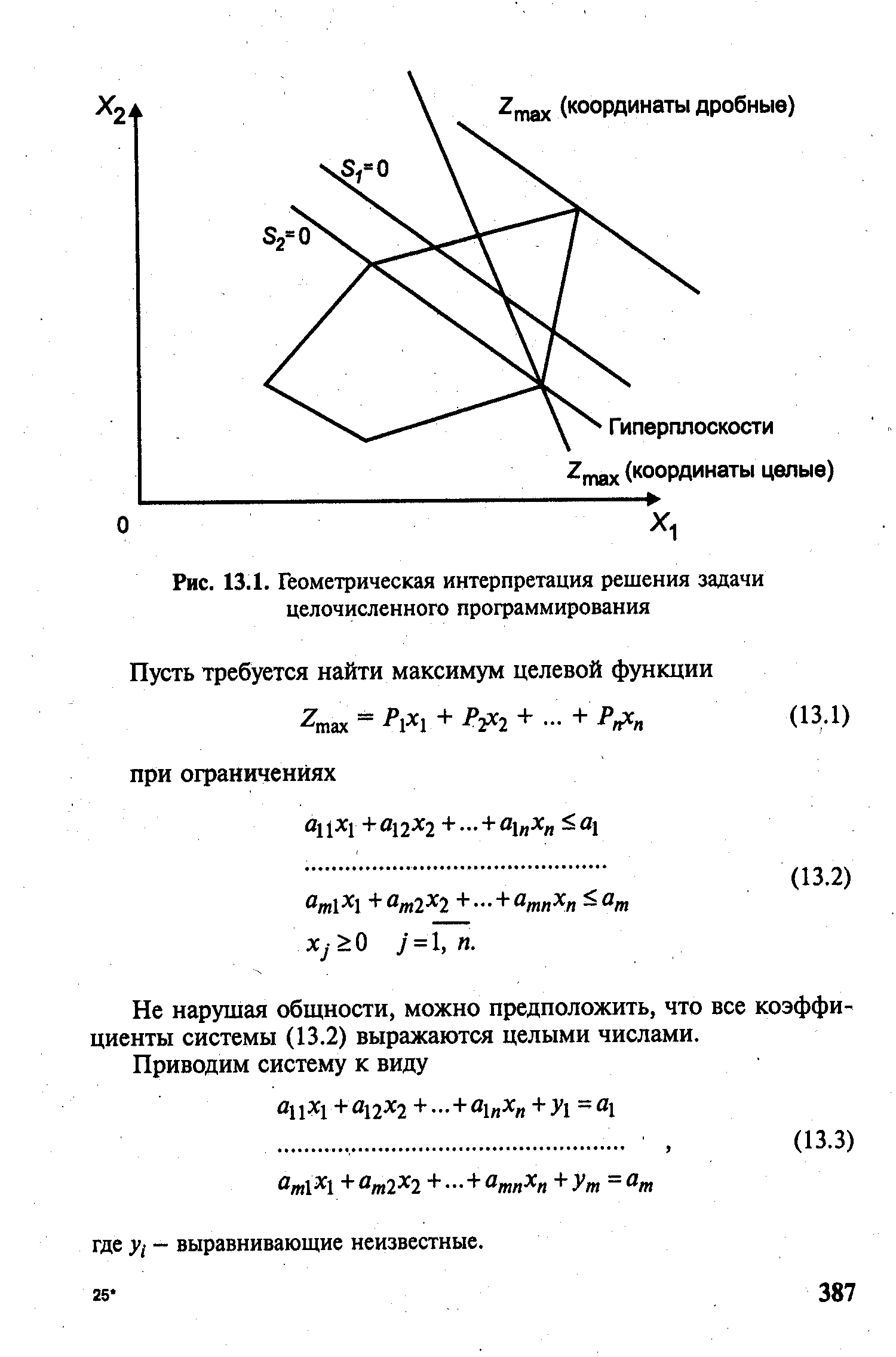 |
МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ [mathemati al programming] (см. также Оптимачьное программирование) — раздел математики, который "... изучает методы решения задач на нахождение экстремума функций (показателя качества решения) при ограничениях в форме уравнений и неравенств"40. Оно объединяет различные математические методы и дисциплины исследования операций линейное программирование, нелинейное программирование, динамическое программирование, выпуклое программирование, геометрическое программирование, целочисленное программирование и др. [c.186]
Обоснованием такого оптимального решения занимается математическое программирование. Суть метода удобнее всего выразить с помощью наглядного геометрического представления, графика (рис. Р.7). Здесь показан построенный по правилам математического программирования многоугольник OAB D (он заштрихован). Многоугольник соответствует условиям нашей задачи и представляет собой область допустимых планов распределения времени работы станков № 2 и № 3 над деталью А. По соответствующим осям графика отмечена продолжительность работы этих станков. (В своих расчетах мы вполне можем обойтись двумя станками и одной деталью, так как по этим данным нетрудно рассчитать и все остальные.) [c.280]
СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (симплекс-метод) [simplex method] — вычислительная процедура, основанная на принципе последовательного улучшения решений — перехода от одной базисной точки (см. Базисное решение) к другой, для которой значение целевой функции больше (эти операции фиксируются в симплексной таблице). Доказано, что если оптимальное решение существует, то оно обязательно будет найдено через конечное число шагов (за исключением т.н. вырожденной задачи, при которой возможно явление "зацикливания", т.е. многократного возврата к одному и тому же положению). Название метод получил от термина " -мерный симплекс". Геометрическая интерпретация метода состоит в последовательном движении по верши) шм симплекса. [c.322]
БАЗА ДАННЫХ — логически организованная совокупность данных (как правило, большая по объему), ориентированная на их эффективное хранение, накопление и обработку (в частности, поиск) с помощью ЭВМ. Для создания и ведения Б.д. используются программные системы управления (СУБД). Организация СУБД на высоком уровне должна опираться на простой и ясный язык общения с Б.д., понятный даже лицу, не знакомому с программированием. На низком же уровне она требует применения сложных алгоритмов, максимально использующих все технические и программные возможности ЭВМ для быстрого и безошибочного исполнения запроса по Б.д. Важнейшие принципы организации Б.д. — иерархический, сетевой и реляционный. Первые два опираются на геометрические представления (представление данных в виде некоторых графов), а последний — на алгебраическую теорию. Однако основополагающие работы Э. Кодда по теории реляционных Б.д. сделали последний принцип их реализации доминирующим. [c.19]
Для технического и математического обеспечения автоматизированных систем проектирования следует решить проблемы широкого внедрения принципов цифрового кодирования геометрической информации и методов обратного преобразования информации в чертежно-графическую разработки математических моделей, методики инженерно-технических и экономических расчетов, используемых в НИР и ОКР, и создания алгоритмов с программами их решения на ЭВМ систематизации математической формализации норм, правил, ТУ, ГОСТов на проектирование для использования их в САПР создания кодированных каталогов изделий, узлов, деталей, материалов, процессов составления кодированных каталогов научно-технической и патентной информации с выводом на копировальные устройства организации автоматизированных архивов, чертежей, справочной и нормативной документации формирования комплексных программ конструирования изделий, их узлов и элементов на базе синтеза частных программ инженерных расчетов выбора и обоснования критериев для принятия оптимальных решений на разных этапах НИР и ОКР алгоритмизации процессов НИ-ОКР, применения эвристических методов и программированных моделей мышления разработчиков разработки методов автоматизации распознавания образов для считывания графической и текстовой информации создания языков для общения ученого и инженера с машиной разработки комплексов технических средств САПР и АСНИ. [c.122]
На первых этапах автоматизированного проектирования довольствовались тем или иным языком программирования, предоставляемым операционной системой ЭВМ. Для автоматизированного проектирования чаще используется ФОРТРАН. В дальнейшем стали создаваться специальные языки и среди них язык представления графической и текстовой информации (ЯГТИ). ЯГТИ используется для описания геометрических и текстовых данных об объекте проектирования независимо от устройств хранения этого описания. По мере развития автоматизированного проектирования создаются языки диалога человека с ЭВМ. Со временем они будут приближаться к обычному разговорному языку и передаваться в форме речи. [c.33]
Паллиативы (метод проекции градиента в общем случае). Выше было показано, что проектирование градиента осуществляется достаточно просто (правда, в линеаризованной постановке, приводящей к проектированию на линейное подпространство) в двух случаях либо при отсутствии дополнительных условий (F(=ff), либо при отсутствии геометрического ограничения на значения и (t) (u( U). Однако большая часть прикладных задач оптимального управления содержит оба сорта условий, а в этом случае проектирование выполняется решением задачи квадратического программирования. К сожалению, идеи и алгоритмы, относящиеся к линейному и нелинейному программированию, мало известны среди специалистов по прикладной механике, которые особенно часто сталкиваются с необходимостью решения задач оптимального управления достаточно общего вида. Именно в этой среде были созданы многочисленные приемы, имеющие целью сформулировать общую задачу как задачу классического типа, либо как простейшую неклассическую задачу. Мы рассмотрим наиболее типичные из этих приемов. Их следует отнести к разряду паллиативов, так как они не снимают трудностей численного решения, а лишь отодвигают их, так сказать, в глубь проблемы. Создание алгоритма приближенного решения задачи оптимального управления можно условно разбить на два этапа [c.160]
