Разделим конечные вершины, в которых пересекаются подграфы, [c.31]
Подграф - часть графа v, образованная подмножеством вершин вместе со всеми [c.127]
Иерархические подграфы, образуемые фиксированной верши- [c.7]
Имена, приписываемые вершинам и ребрам, обычно совпадают с именами соответствующих сущностей и отношений, используемыми в естественном языке. Ребро и связываемые им вершины образуют подграф СС, несущий минимальную с позиций знаний системы информацию — факт наличия связи определенного типа между соответствующими объектами. Более сложные подграфы отображают и более сложные факты. [c.562]
Г. называется связным, если для каждой пары вершин существует соединяющая их цепь или путь (последовательность ребер). В противном случае он называется несвязным. Г. может разделяться на подграфы, причем связный подграф называется компонентой исходного Г. [c.67]
В обоих случаях главное понятие теории — граф, изучаемый как абстракция, независимо от его содержания. Напр., карта Московской кольцевой дороги и подходящих к ней радиальных магистралей — это точно такой же по своей природе граф, как диаграмма, с помощью которой изучаются потоки зрителей, выходящих из цирка после представления. С графами приходится иметь дело на каждом шагу схемы, диаграммы, карты дорог, линии связи, фигуры, даже структуры химических соединений — все это наглядные примеры графов. Т.г. изучает качественные и количественные связи и соотношения между элементами графов с разных точек зрения (структурной, информационной и т.д.). Напр., выясняется связность графа, т.е. возможность попасть из любой его вершины в любую другую формируются правила расчленения графов на части (подграфы) и, наоборот, композиции ("сшивания") графов в более крупные, в том числе синтез графов с заданными свойствами. Исследование графов [c.355]
Под распараллеливанием вычислительных алгоритмов будем понимать распределение операций этого алгоритма по процессорам, а в графовых представлениях — вершин графа ГА по подграфам, общее число которых равно р и каждому из которых соответствует один из процессоров (одна из вершин ГС), Такое распределение будем представлять в виде матрицы разрезания R размерности рхп, элементы г которой равны 1 — если [c.141]
Элементы такой матрицы определяют суммарный вес вершин, принадлежащих /-му подграфу и k-му ярусу в ГА. Время на выполнение межпроцессорных обменов информацией будет определяться объемом дуг, соединяющих вершины, принадлежащие разным подграфам. Для вычисления [c.142]
Оптимизационную задачу распараллеливания вычислений сформулируем следующим образом. Пусть заданы ГА=(и, с, S) и ГС=(р, п, ц). Найти матрицу разрезания R графа ГА на р подграфов, дающую минимум функционалу J(R). [c.143]
Часть I 3.3. СТОХАСТИЧЕСКИЙ МЕТОД ПОПАРНОЙ ОПТИМИЗАЦИИ ПОДГРАФОВ [c.148]
Выбираем пару подграфов с номерами /, j с вероятностью пропор- [c.148]
Случайно выбираем пару вершин 1 и т в этих подграфах (таким образом перебираются все пары вершин в этих подграфах) меняем местами эти вершины, получаем новое разрезание R, вычисляем [c.148]
Описанный алгоритм является итерационным. Внешние итерации связаны с попарным просмотром подграфов, а внутренние — с просмотром вершин в этих подграфах. Переход от разрезания к разрезанию происходит, если выполняется условие перехода 5. [c.148]
Исследование на точность метода проводилось для алгоритмов сдваивания с N = 8 при разрезании их на р = 4, 8 подграфов. Было проведено по 70 опытов для каждого случая. На рис. 1. 45 изображена функция распределения / относительной погрешности для этих двух случаев. [c.148]
| Рис. 1.45. Функция распределения / относительной погрешности 5 алгоритма А1 при разрезании графа сдваивания с п = 15 на 1) р = 4 2) р = 8 подграфов | 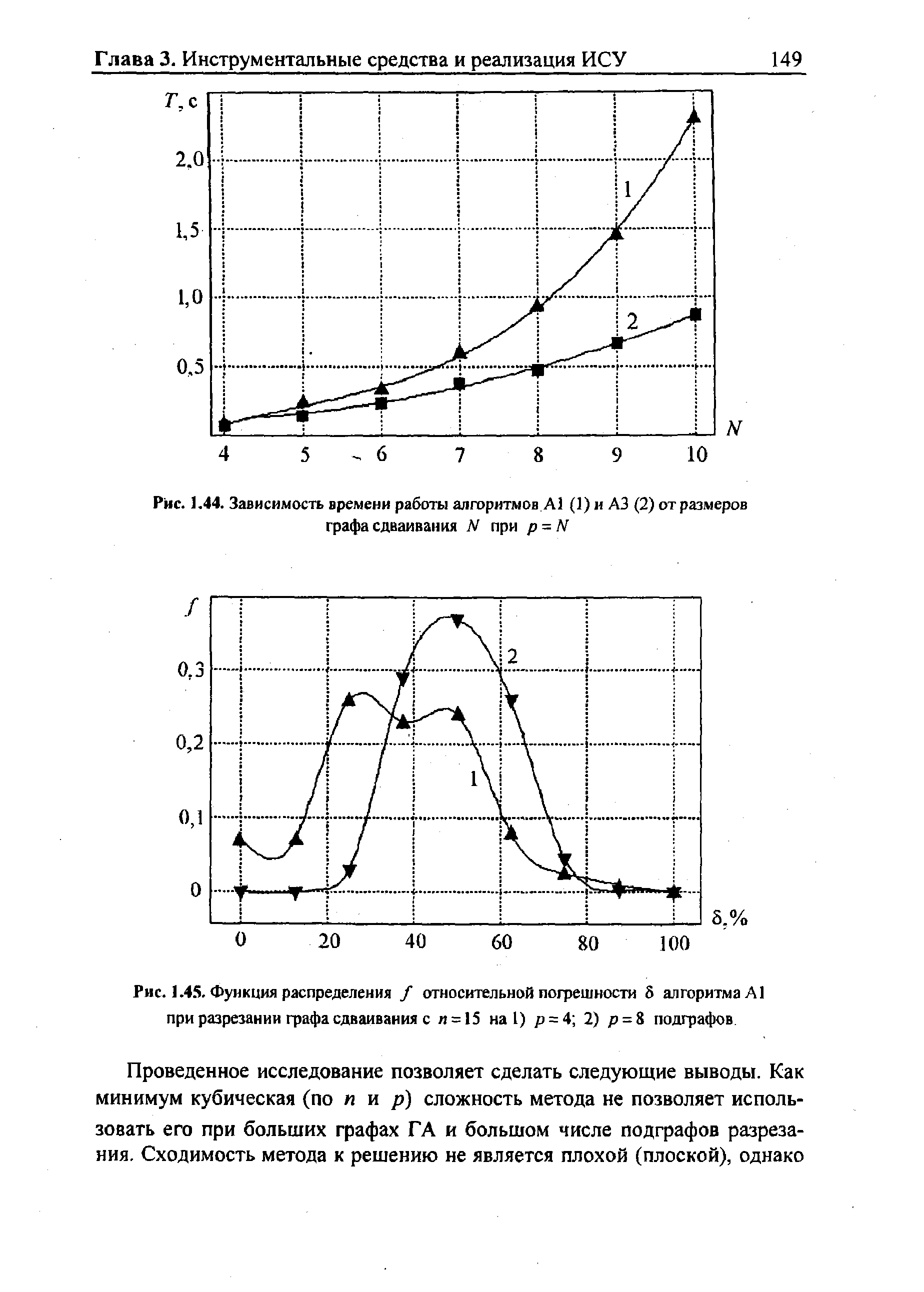 |
Проведенное исследование позволяет сделать следующие выводы. Как минимум кубическая (no n и р) сложность метода не позволяет использовать его при больших графах ГА и большом числе подграфов разрезания. Сходимость метода к решению не является плохой (плоской), однако [c.149]
Выбираем подграфы, связность которых с 1 равна. [c.150]
Вершину 1 заносим в тот из выбранных подграфов, который имеет наименьший вес и переходим на 1. [c.150]
Алгоритм заканчивает работу, когда все вершины распределены по подграфам. Было проведено аналогичное исследование алгоритма A3 (метод А1 с выбором начального разрезания А2) на сложность, сходимость и точность. Результаты исследования представлены на рис. 1.44, 1.46. Выигрыш по сравнению с А1 очевиден. Уменьшилась сложность алгоритма. Улучшилась точность метода. Зато оказалась очень плоской зависимость функционала J по итерациям. Это объясняется тем, что алгоритм А2 в большинстве случаев сразу приводит к локальному минимуму. [c.150]
| Рис. 1.46. Функция распределения / относительной ошибки S алгоритма A3 при разрезании графа сдваивания с и = 15 на ) / = 4 2) р = подграфов | 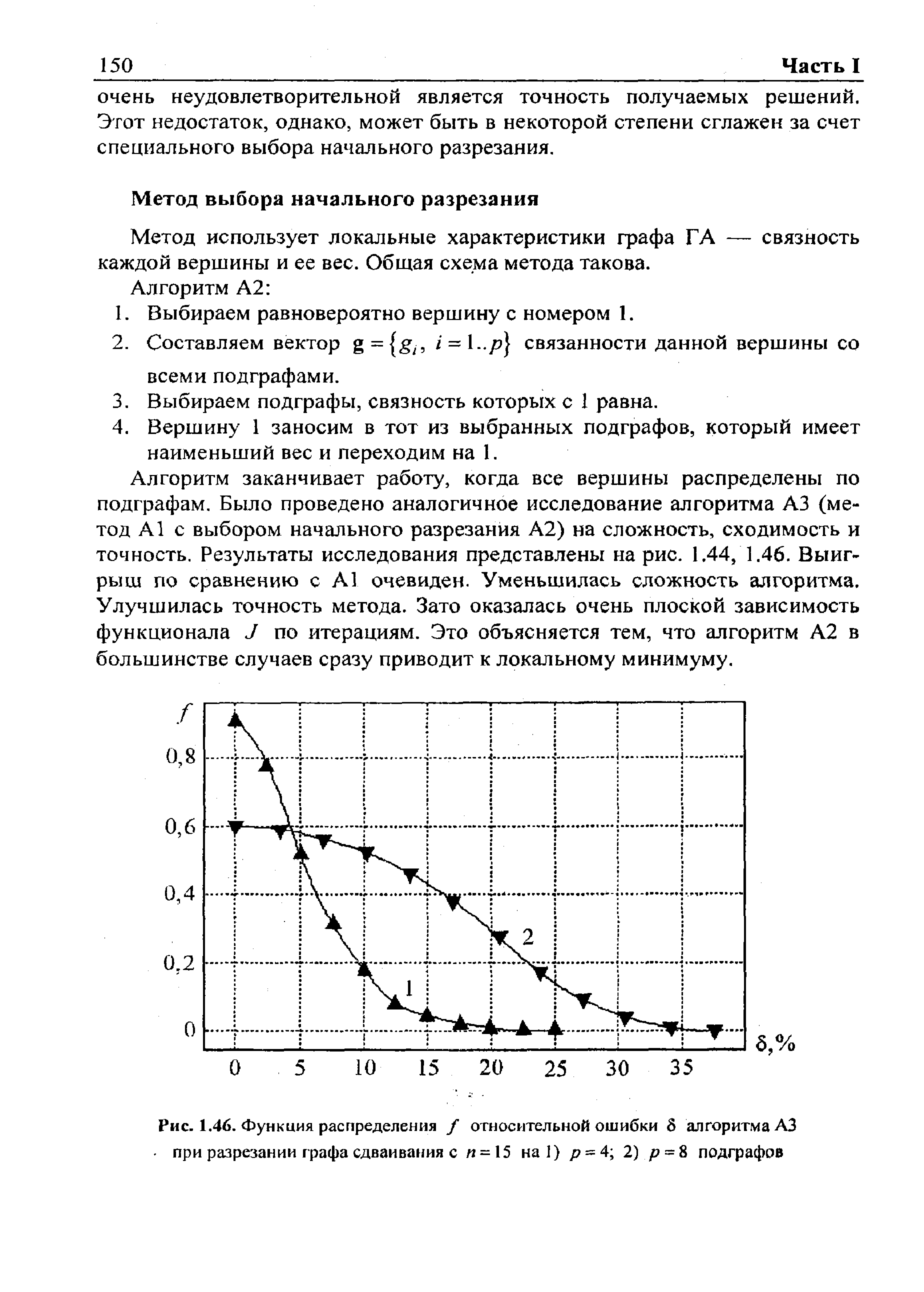 |
На каждой итерации t случайным образом перебираем все частицы-вершины. Для каждой из вершин случайно выбираем новый подграф и определяем приращение функционала Л У при переносе в него данной вершины. Если Л J < О, то вершина переносится в новый подграф, иначе она переносится в него с вероятностью ехр(-ДУ/б). [c.152]
На рис, 1.49 отражены результаты сравнительного анализа предложенного алгоритма и алгоритма попарной оптимизации подграфов A3. Изображена зависимость времени работы алгоритмов от р при ГА = В(8р, 1). Кривая 1 соответствует времени работы алгоритма попарной оптимизации, а кривая 2 — времени работы алгоритма Монте-Карло по достижении точности, достигнутой при реализации метода A3. Видно преимущество подхода, основанного на методе Монте-Карло, при решении больших задач распараллеливания. [c.155]
На каждой итерации t случайным образом перебираем все частицы-вершины. Для каждой из вершин определяем вектор значений функционала J, при переносе данной вершины во все подграфы. Случайным образом перемещаем вершину в другой подграф, при этом вероятность переноса вершины в /-ый подграф равна [c.155]
В [87] описывается очень популярный в последнее время метод решения различных дискретных задач оптимизации — метод имитации отжига, являющийся модификацией известного алгоритма Метрополиса. В [87] решается задача о разбиении графа на два подграфа с равным числом вершин и с минимальным числом ребер, соединяющих эти подграфы. Эта задача соответствует задаче назначения с р = 2. Вершины графа трактуются [c.147]
Под действием поля частицы — вершины графа — будут стремиться расположиться по подграфам так, чтобы доставить минимум функционалу /. Однако расчет координат по детерминистическому уравнению (1.155) может привести к попаданию частиц в один из локальных минимумов, из которого они не в состоянии выбраться. Поэтому в систему вводятся дополнительные стохастические силы, приводящие к тепловым флюктуаци-ям частиц, которые помогают им выбраться из локальных минимумов. Тогда процесс поиска оптимального расположения частиц в подграфах будем моделировать процессом случайного блуждания в потенциальном силовом поле J(R). Пусть вероятность P(R,f) обнаружить частицу в момент t в точке с координатами R подчиняется уравнению Фоккера-Планка [c.151]
Максимум вероятности (1.157) соответствует такому расположению частиц по подграфам, которое доставляет минимум функционалу J. Соотношение Эйнштейна D = у9 связывает подвижность у и коэффициент диффузии Q, характеризующий тепловые флюктуации. Распределение (1. 157) является распределением Больцмана с температурой 6. [c.152]
Смотреть страницы где упоминается термин Подграф
: [c.84] [c.17] [c.19] [c.27] [c.29] [c.31] [c.31] [c.128] [c.7] [c.80] [c.51] [c.90] [c.90] [c.90] [c.266] [c.481] [c.141] [c.143] [c.147] [c.147] [c.148] [c.148] [c.150]Ситуационное управление теория и практика (1986) -- [ c.205 ]
