Марковские цепи

из "Математические методы моделирования экономических систем Изд2 "

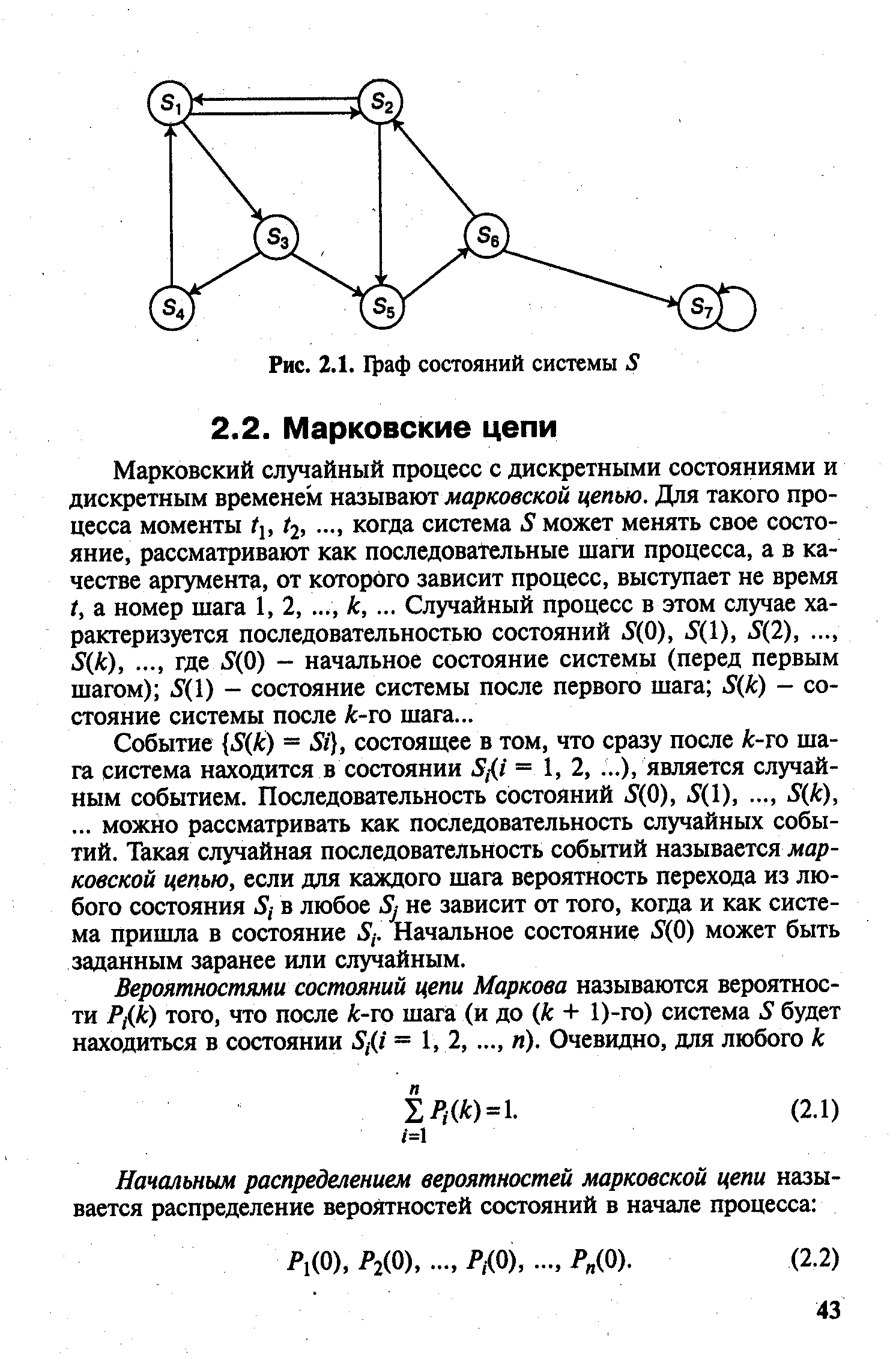
Марковский случайный процесс с дискретными состояниями и дискретным временем называют марковской цепью. Для такого процесса моменты fj, /2,. .., когда система S может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время t, а номер шага 1, 2,. .., k,. .. Случайный процесс в этом случае характеризуется последовательностью состояний 5(0), S(l), 5(2),. .., S(k),. .., где 5(0) — начальное состояние системы (перед первым шагом) 5(1) - состояние системы после первого шага S(k) - состояние системы после Л-го шага... [c.43]
Событие (S(k) — Si , состоящее в том, что сразу после k-то шага система находится в состоянии 5Д/ - 1, 2,. ..), является случайным событием. Последовательность состояний 5(0), 5(1),. .., S(k),. .. можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния 5,- в любое Sj не зависит от того, когда и как система пришла в состояние 5,-. Начальное состояние 5(0) может быть заданным заранее или случайным. [c.43]
В частном случае, если начальное состояние системы S в точности известно (0) = Sj, то начальная вероятность Pj(0) = 1, а все остальные равны нулю. [c.44]
Вероятностью перехода (переходной вероятностью) на k-u шаге из состояния Si в состояние S/ называется условная вероятность того, что система S после k-ro шага окажется в состоянии А при условии, что непосредственно перед этим (после k — 1 шага) она находилась в состоянии Sj. [c.44]
Матрица (2.3) называется переходной или матрицей переходных вероятностей. [c.44]
Если переходные вероятности не зависят от номера шага (от времени), а зависят только от того, из какого состояния в какое осуществляется переход, то соответствующая цепь Маркова называется однородной. [c.44]
Пример 2.1. Рассмотрим процесс функционирования системы автомобиля. Пусть автомобиль (система) в течение одной смены (суток) может находиться в одном из двух состояний исправном (S ) и неисправном (S2). Граф состояний системы представлен на рис. 2.2. [c.45]
Вектор начальных вероятностей состояний автомобиля задан Р(0) = И, т.е. /1(0) = 0 и/ (0) = 1. [c.45]
Требуется определить вероятности состояний автомобиля через трое суток. [c.46]
Таким образом, после третьих суток автомобиль будет находиться в исправном состоянии с вероятностью 0,819 и в состоянии неисправен с вероятностью 0,181. [c.46]
Определите вероятности состояний ЭВМ после трех проверок. [c.47]
Граф состояний имеет вид, показанный на рис. 2.3. Против каждой стрелки проставлена соответствующая вероятность перехода. Начальные вероятности состояний Pj(0) = 1 Р2(0) = P (Q) - Р4(0) 0. [c.47]
вероятности состояний ЭВМ после трех проверок следующие Р З) - 0,027 Р2(3) = 0,076 Р3(3) - 0,217 Р4(3) = 0,680. [c.47]

Вернуться к основной статье