Модель 2 (метод цепей Маркова). При построении общего алгоритма воспользуемся тем же подходом, что и в модели 1, то есть при фиксированном k найдем распределение с.в. щ, HI, И2, из. Вычисление показателей надежности в конечном счете проведем с помощью формулы полной вероятности (2.1.8). Однако для поиска распределений с.в. и, (z= =0, 1, 2, 3) будем пользоваться не комбинаторными методами, а методом марковских цепей. [c.117]
Общее число состояний J марковской цепи, вероятность которых в принципе может быть отлична от 0, не очень велико, поскольку переменные и, (/ = 0,1,2,3) удовлетворяют соотношениям (2.1.4), (2.1.5). [c.118]
Процесс o(t) предполагается нестационарной марковской цепью, начальное состояние которой га(0) = сцз считается известным. Множество /2(/) состояний процесса конечно. Оно может формироваться для каждого t — 1,..., Т экспертом или программой с учетом следующих известных взаимосвязей между макроэкономическими показателями [72,95,96] [c.261]
| Рис.4.1 Переходы между состояниями марковской цепи эволюции макросреды Распределение переходных вероятностей на различных временных срезах характеризует уровень доверия эксперта к экономическим действиям существующего и будущих правительств. Оценки эксперта позволяют построить марковский прогноз развития экономической ситуации. Иллюстративный прогноз на 2001-2005 гг. в предположении, что в настоящее время Россия испытывает период стагнации, представлен в табл. 4.2. В последней графе приведено стационарное распределение марковской цепи, которое практически достигается уже через 6 лет. Из прогноза видно, что, если так пойдет и впредь, то вероятность кризисов и периодов быстрого роста достаточно велика и ее нельзя сбрасывать со счетов. Отметим, что даже в столь простом случае цепь содержит 55=3125 различных траекторий, то есть сценариев, каждый из которых имеет вероятность реализации, не превышающую 0,00032. | 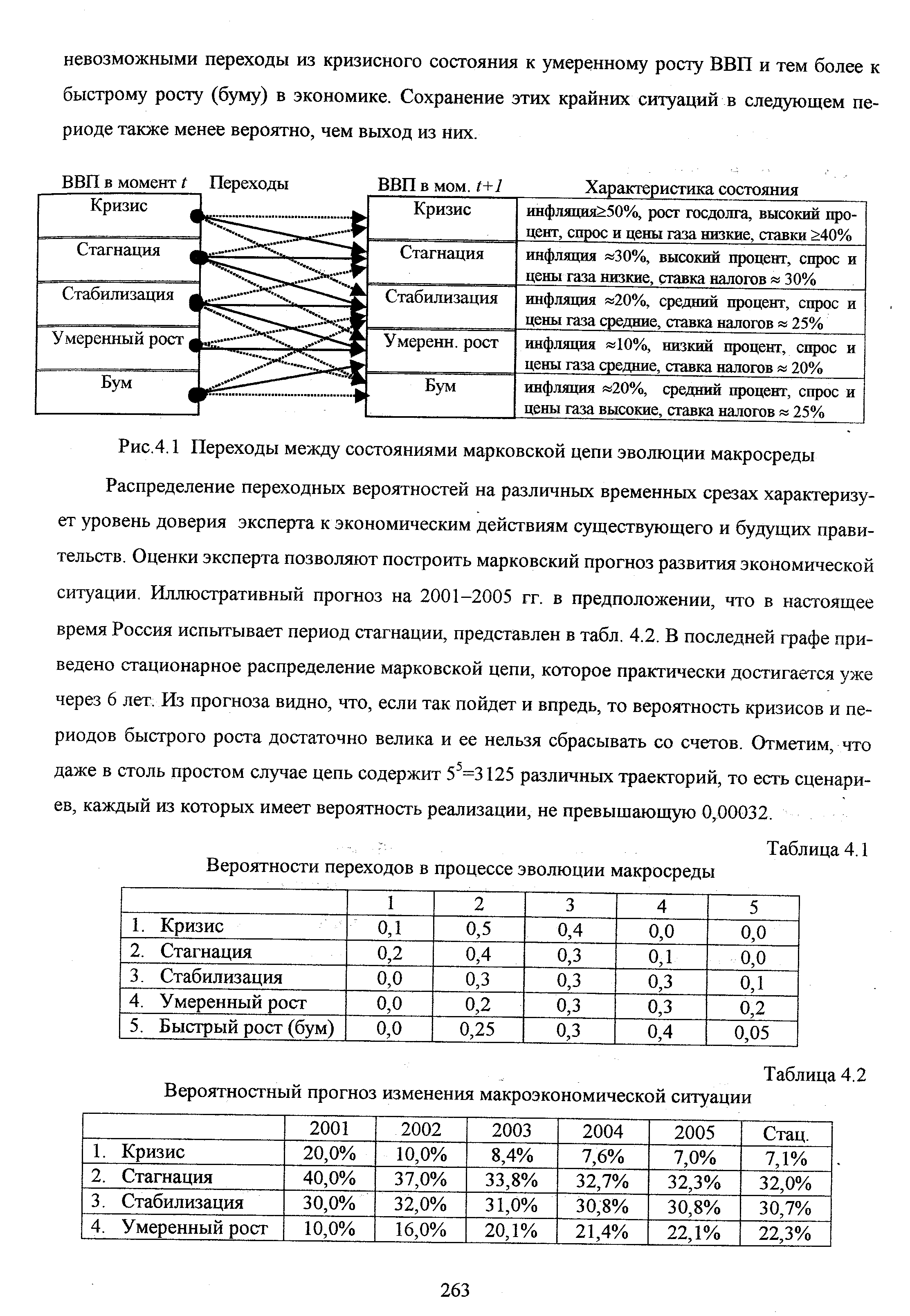 |
Обсуждение и выводы. Принципиальное отличие предлагаемого подхода от традиционных состоит в использовании многоэтапной стохастической процедуры выбора стратегии развития, в которой стратегия рассматривается как набор "решающих правил", которые определяют оптимальное поведение компании во всех возможных состояниях в будущем. Решение определяет марковскую цепь, которая дает вероятностный прогноз эволюции состояния СТГ и финансового положения компании в зависимости от развития макроэкономических показателей внешней среды. Процедура имитирует процесс принятия решений в зависимости от текущей ситуации. Сейчас и в будущем компания выбирает свою стратегию, зная лишь текущее состояние СТГ и макросреды при гипотетическом вероятностном прогнозе будущего. [c.273]
Центральным является предположение о том, что в любом состоянии на каждом шаге компания стремится к максимизации математического ожидания результата на оставшемся отрезке времени. Решением является выбор для каждого состояния <%t) марковской цепи оптимального управления u(f), то есть номеров тех проектов (из портфеля), реализацию которых компания должна начать в момент попадания в данное состояние. Если компания примет эту стратегию, то ей гарантируется на оставшемся промежутке времени максимум среднего (ожидаемого) эффекта. [c.274]
После выбора оптимального реализуемого варианта вывода нового товара (услуги) на рынок руководству фирмы необходимо принять решение какую принять политику сбыта, как развиваться на рынке, как увеличить долю рынка этого товара, чтобы в конечном счете возросла прибыль. При этом должно быть гарантировано получение надежной информации для принятия объективного решения. Естественно, что любой выбранный вариант освоения новинки принесет фирме трудно предсказуемый результат. Для уменьшения этой неопределенности можно рассматривать и анализировать перспективу деятельности фирмы с использованием теории марковских цепей и теории принятия решений Байеса. [c.183]
Марковский случайный процесс с дискретными состояниями и дискретным временем называют марковской цепью. Для такого процесса моменты fj, /2,. .., когда система S может менять свое состояние, рассматривают как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, выступает не время t, а номер шага 1, 2,. .., k,. .. Случайный процесс в этом случае характеризуется последовательностью состояний 5(0), S(l), 5(2),. .., S(k),. .., где 5(0) — начальное состояние системы (перед первым шагом) 5(1) - состояние системы после первого шага S(k) - состояние системы после Л-го шага... [c.43]
Событие (S(k) — Si , состоящее в том, что сразу после k-то шага система находится в состоянии 5Д/ - 1, 2,. ..), является случайным событием. Последовательность состояний 5(0), 5(1),. .., S(k),. .. можно рассматривать как последовательность случайных событий. Такая случайная последовательность событий называется марковской цепью, если для каждого шага вероятность перехода из любого состояния 5,- в любое Sj не зависит от того, когда и как система пришла в состояние 5,-. Начальное состояние 5(0) может быть заданным заранее или случайным. [c.43]
Начальным распределением вероятностей марковской цепи называется распределение вероятностей состояний в начале процесса [c.43]
Переходные вероятности однородной марковской цепи Ру образуют квадратную матрицу размера п х п. Отметим некоторые ее особенности [c.44]
Если для однородной марковской цепи заданы начальное распределение вероятностей (2.2) и матрица переходных вероятностей Py (2.3), то вероятности состояний системы P, k) (i = l,n j =l,n) определяются по рекуррентной формуле [c.45]
В начальный момент времени ЭВМ полностью исправна (состояние iSj). Проверка ЭВМ производится в фиксированные моменты времени fj, /2> /3- Процесс, протекающий в системе S, может рассматриваться как однородная марковская цепь с тремя шагами (первая, вторая, третья проверки ЭВМ). Матрица переходных вероятностей имеет вид [c.46]
При исследовании непрерывных марковских цепей, как было уже отмечено, часто бывает удобно представить переход системы из состояния в состояние как воздействие каких-то потоков событий (поток заявок на обслуживание, поток автомобилей, поток документов и т. п.). Различают следующие основные свойства, которыми могут обладать случайные потоки событий [c.53]
Рассмотрим еще одну типичную схему непрерывных марковских цепей, так называемую схему гибели и размножения, часто встречающуюся в разнообразных практических задачах. [c.55]
Марковские цепи 43, 48 Матрица переходных вероятностей 44 [c.425]
Если е = (en)n>i последовательность независимых случайных величин, ho не зависит от е = (en)n i, то последовательность /i = (/in)n i будет классическим примером конструктивно заданной марковской цепи. Рекуррентным образом из (6) находим [c.157]
Марковский случайный процесс с дискретными состояниями и дискретным временем обычно называют марковской цепью. Для такого процесса моменты времени г,, t2,. .., когда система S может менять свое состояние, удобно рассматривать, как последовательные шаги процесса, а в качестве аргумента, от которого зависит процесс, рассматривать не время t, а номер шага 1, 2,. .., /с,. ... [c.147]
Марковская цепь называется однородной, если переходные вероятности не зависят от номера шага (т. е. от момента времени tk), а зависят только от того, из какого состояния и в какое осуществляется переход. В дальнейшем мы ограничимся рассмотрением однородных марковских цепей. [c.147]
Распределение вероятностей состояний в начале процесса Р,(0), Р2(0),. .., Р(0),. .., Р (0) называется начальным распределением вероятностей марковской цепи. [c.151]
Формализация модели. Проанализируем динамику переходов системы из одного состояния в другое в процессе времени, т. е. построим марковские цепи, рассчитывая одновременно соответствующие вероятности переходов. [c.156]
Определение 2.3. Случайная последовательность называется марковской цепью, если для каждого шага вероятность перехода из любого состояния у в любое состояние s.He зависит от того, когда и как система S оказалась в состоянии sf [c.22]
Основными характеристиками марковских цепей являются вероятности (k) = pdS k)) (i=l,. .., п k=l,2,. ..) событий St(k). [c.23]
Если же хотя бы одна вероятность изменяется с изменением шага k, то марковскую цепь называют неоднородной. [c.24]
В этой главе мы рассмотрим однородные марковские цепи. Запишем переходные вероятности в виде квадратной матрицы и-го порядка [c.24]
Теорема 2.1. Для однородной марковской цепи вектор-строка вероятностей состояний от k-го до (k+ )-to шага равна произведению вектор-строки вероятностей состояний от (k-l)-zo до k-го шага на матрицу пере ых вероятностей [c.26]
Следствие 2.1. Для однородной марковской цепи имеет место следующая формула [c.28]
Таким образом, в системе S протекает однородный марковский дискретный случайный процесс с дискретным временем, т.е. имеем однородную марковскую цепь. [c.29]
У однородной марковской цепи переходные вероятности постоянны, не зависят от шагов (практически каждая переходная вероятность на любом шаге пренебрежимо мало отличается от постоянной для нее величины). [c.31]
Основными вероятностными прогнозными характеристиками марковской цепи являются вероятности состояний на любом шаге p. (k), г=1, 2..... [c.32]
Что такое марковская цепь [c.32]
Дайте определение однородной марковской цепи. [c.33]
Одной из основных моделей случайных процессов, используемой в прогнозировании, является модель марковских цепей. Такими моделями, которые могут быть включены в системы поддержки принятия решений, описывается большое количество физических, биологических, экономических, технических и других явлений. Применительно к нефтяной и газовой промышленности - это процессы технического обслуживания и ремонта нефтяных и газовых скважин, объектов транспорта нефти и газа, оборудования нефте-(газо)перерабатывающих заводов процессы планирования и организации проведения геолого-технических мероприятий и геофизических исследования скважин, управления запасами и др. [c.339]
Нами построены 3 модели для расчета показателей надежности комплекса дожимных станций ГДП. Первая модель использует лишь случайные величины, вторая - аппарат марковских цепей и третья - метод Монте-Карло. Отпишем первые две, опустив третью, так идеи имитационного моделирования стандартны. [c.115]
Эксперт пользуется также предположением, что распределения переходных вероятностей не зависят от времени 7ty(f)=P a(t+r)=j aj(i)=i = onst, ie %t), j f t+l) и марковская цепь однородна. Из представленных в табл. 4.1 распределений видно, что эксперт считает [c.262]
Совокупность ограничений на состояния и управления для каждого периода [ , + ] в векторной форме принимает вид G (t, )>0, t = 0,1,..., Т. В каждый момент времени t агрегат "внешняя среда и система" находится в состояниях из фазового множества E(t, U). Например, если реконструкция или строительство объекта осуществляется за один период [t, t+l], то переход системы (агрегата) из произвольного состояния i
Определение 2.6. Если переходные вероятности не зависят от шагов k, то марковская цепь называется одно юдной. [c.24]
Процесс с дискретным временем процесс с непрерывным временем случайная последовательность марковская цепь вероятности состояний переходные вероятности матрица переходных вероятностей вероятности задержки однородная марковская цепь стохастическая матрица двоякосто-хастическая матрица размеченный граф состояний вектор начального распределения вероятностей. [c.32]
Смотреть страницы где упоминается термин Марковские цепи
: [c.182] [c.15] [c.101] [c.147] [c.270] [c.43] [c.290] [c.130]Смотреть главы в:
Математические методы моделирования экономических систем Изд2 -> Марковские цепи
