Сущность инвестиционного риска. Классификация инвестиционных рисков. Источники риска. Систематическая и несистематическая компонента риска инвестиций. Способы оценки риска. Статистический метод, метод Монте-Карло, экспертный метод, метод чувствительности. [c.82]
Теории массового обслуживания, статистических испытаний (или метод Монте-Карло) и статистических решений применимы для решения организационных задач. [c.152]
На практике возникает большое число задач, где необходимо определить оптимальный способ организации работ и использования оборудования. В этом случае применяют имитационные модели, заключающиеся в имитации экономических и производственных условий на ЭВМ путем воспроизведения элементарных явлений и актов процесса в последовательности, содержащей реальные связи и взаимосвязи. Из методов статистического моделирования используются метод Монте-Карло, сетевые модели и др. Содержание и методика использования конкретных моделей рассматривается далее. [c.19]
Планировку участка предметной специализации определяют по ведущему технологическому процессу, а при его отсутствии — по критерию оптимальности. На участках изготовления изделий электронной техники таким критерием могут быть минимальный объем незавершенного производства, наименьшая длительность процессов изготовления изделия, минимальная себестоимость. При этом целесообразно использование методов статистического моделирования (метода Монте-Карло, метода направленного перебора, обеспечивающего путем перестановок приближение к оптимуму с помощью транспозиций матриц). [c.114]
Метод Монте-Карло может быть использован при решении вопроса о рациональности использования бурового оборудования, определении мощности производственных процессов, оптимальных условий работы. [c.89]
Для анализа стохастических моделей, особенно многокритериальных, в последнее время широко используется подход имитационного типа, получивший название метода Монте-Карло. Он состоит в следующем с помощью специально реализованного в ЭВМ генератора случайных чисел строят последовательность чисел г/ , г/2, . ., UN, которые в совокупности можно интерпретировать как последовательность реализаций случайной величины у. Выбирают конечное число вариантов управления xt, xz,. . ., хп. Рассчитывают значения W(xt, ys) для всех i = 1,. . ., п j = 1,. ... . ., N. Числа W(xi, z/j) (/ = 1,. . ., N) дают представление о распределении показателя W при управлении xt, т. е. о функции распределения FXi(r ), и могут использоваться для оценки этого [c.155]
Для того чтобы хорошо оцепить распределение FXi(r ), необходимо взять достаточно большое значение. /V — числа реализации случайной величины у. Чтобы хорошо аппроксимировать множество всех решений X, приходится брать большое число п. Это приводит к очень большому (п X N) числу расчетов, что делает метод Монте-Карло не всегда реализуемым на практике. Все же, несмотря на описанный недостаток, метод используется очень часто, поскольку является во многих случаях единственным пригодным средством анализа модели. [c.155]
К сожалению, при непосредственном применении методов теории вероятностей исследовать достаточно сложные системы удается не всегда. В таком случае приходится прибегать к имитационным экспериментам на вычислительной машине, которые в данном случае называются методами Монте-Карло. [c.205]
Наиболее распространенными методами анализа рисков являются анализ чувствительности (уязвимости), анализ сценариев и моделирование рисков по методу Монте-Карло. [c.322]
МЕТОД МОНТЕ-КАРЛО. Этот метод воссоединяет методы анализа чувствительности и анализа сценариев на базе вероятностного подхода. Он достаточно сложен, его реализация возможна только при помощи компьютера. Итог такого анализа — распределение вероятностей возможных результатов проекта (например, вероятность получения А/РУ < 0), на основании чего принимают решение о степени рисковости данного проекта. [c.323]
Определение оптимального уровня денежных средств. Смысловая нагрузка последнего блока определяется необходимостью нахождения компромисса между, с одной стороны, желанием обезопасить себя от ситуаций хронической нехватки денежных средств и, с другой стороны, желанием вложить свободные денежные средства в какое-то дело с целью получения дополнительного дохода. В мировой практике разработаны методы оптимизации остатка денежных средств, в основе которых заложены те же идеи, что и в методах оптимизации производственных запасов. Наибольшую известность получили модели Баумоля, Миллера — Орра, Стоуна и имитационное моделирование по методу Монте-Карло [Ковалев, 1999]. Суть данных моделей состоит в том, чтобы дать рекомендации о коридоре варьирования остатка денежных средств, выход за пределы которого предполагает либо конвертацию денежных средств в ликвидные ценные бумаги, либо обратную процедуру. [c.375]
Получение характеристик систем массового обслуживания подобного класса возможно с помощью метода статистических испытаний — метода Монте-Карло, т.е. путем создания имитационной модели, на которой проигрывают различные ситуации, возникающие в процессе выполнения оперативного плана. [c.232]
Наиболее сложным, трудоемким и дорогостоящим методом анализа рисков является метод Монте-Карло. Он, в основном, используется для анализа рисков крупных проектов в условиях недостаточного объема априорной информации. Этот метод заключается в построении имитационных моделей, позволяющих создать множество сценариев, согласующихся с заданными ограничениями на исходные переменные. [c.281]
Рассмотрим следующий модельный пример. Методом Монте-Карло (см. 12.2) была сымитирована модель [c.214]
Метод Монте-Карло [c.285]
Эксперимент по методу Монте-Карло — это эксперимент, основанный на компьютерном моделировании случайных величин. [c.285]
Суть метода Монте-Карло заключается в том, что с помощью компьютера можно многократно наблюдать случайную величину с заранее известным распределением. Это позволяет получить (или проверить) статистические результаты экспериментально. [c.285]
В эконометрическом моделировании значение метода Монте-Карло особенно велико. С его помощью можно построить модель с заранее известными параметрами (отметим еще раз, что в реальных моделях параметры никогда не бывают известны). [c.286]
Метод Монте-Карло позволяет проверить экспериментально результаты, полученные теоретически. В качестве примера рассмотрим задачу выбора спецификации модели. Пусть имеются фиксированные выборки переменных X, Z, а случайные выборки переменной К генерируются по формуле [c.286]
С помощью метода Монте-Карло можно наглядно демонстрировать результаты применения тестов, а также экспериментально оценить последствия нарушения тех или иных условий. [c.287]
Наконец, отметим особенно значимую роль экспериментов по методу Монте-Карло в процессе обучения. Именно с помощью таких экспериментов можно увидеть различия между методами оценивания моделей, наблюдать эффекты, вызванные нарушением тех или иных условий и т. д. [c.287]
С помощью метода Монте-Карло построить следующие величины [c.287]
Методом Монте-Карло сгенерировать следующие временные ряды [c.288]
С помощью теории массового обслуживания можно получить аналитические выражения и при других дисциплинах обслуживания очереди и конфигурациях вычислительной системы. Рассматривая модель обслуживания заданий, мы исходим из предположений того, что процессы в системе - марковские, а потоки - простейшие. Если эти предположения неверны, то получить аналитические выражения трудно, а чаще всего невозможно. Для таких случаев моделирование проводится с помощью метода статистических испытаний (метода Монте-Карло), который позволяет создать алгоритмическую модель, [c.76]
Наиболее часто встречающимися методами количественного анализа рисков проекта, как уже отмечалось, являются анализ чувствительности (уязвимости), анализ сценариев и имитационное моделирование рисков по методу Монте-Карло. [c.213]
| Рис. 7.6. Анализ рисков (по методу Монте-Карло) | 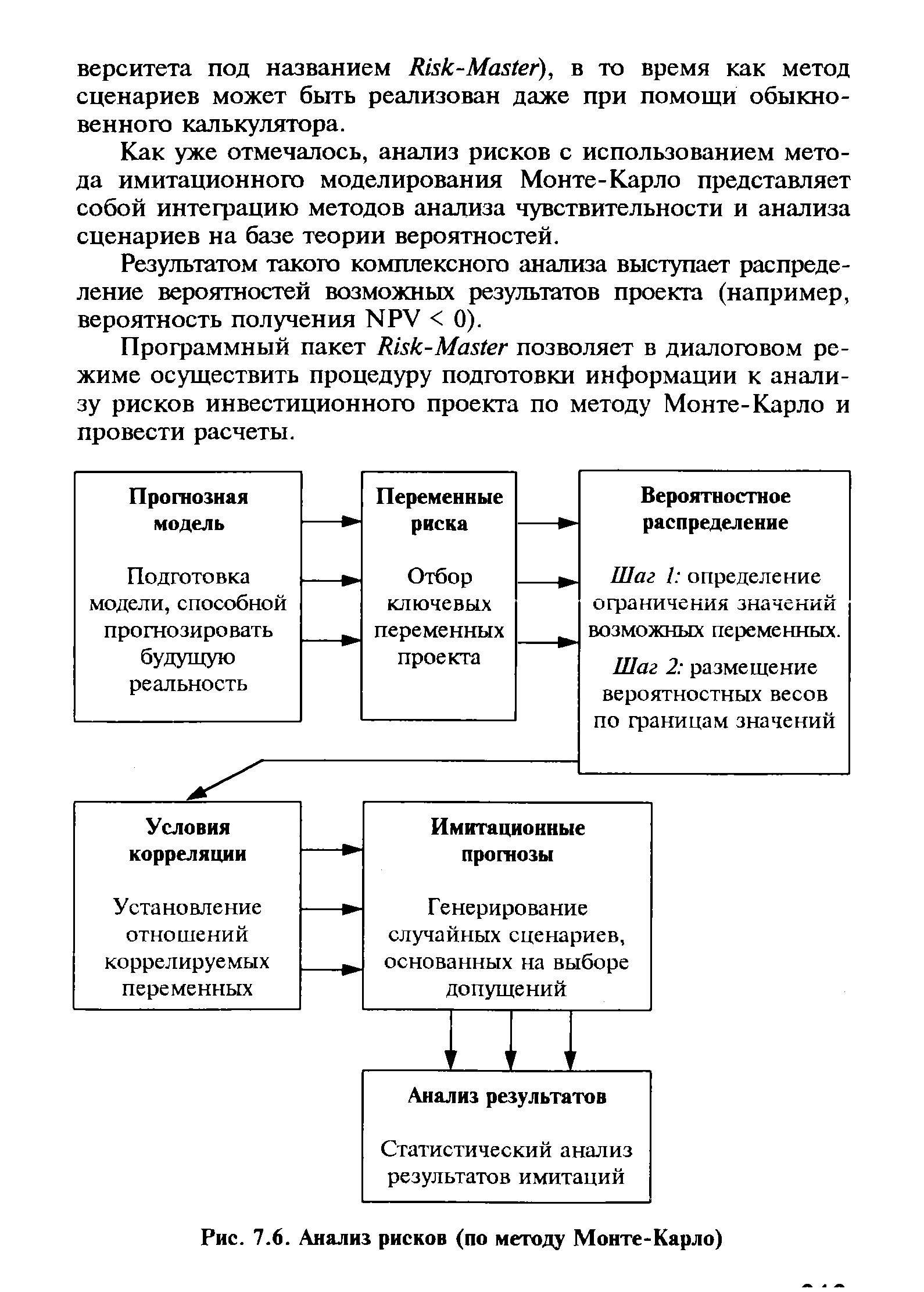 |
В результате анализа, проведенного методом Монте-Карло, эксперт получает значение ожидаемой чистой приведенной стоимости проекта и плотность распределения этой случайной величины. Однако этих данных недостаточно для того, чтобы аналитик установил, действительно ли прибыльность проекта настолько велика, что компенсирует риск по проекту, оцененный стандартным отклонением и коэффициентом вариации. Ряд исследователей избегает использования данного метода ввиду сложности построения вероятностной модели и множества вычислений, однако при корректности модели метод дает весьма надежные результаты, позволяющие судить как о доходности проекта, так и о его устойчивости (чувствительности). [c.252]
Каковы основы анализа рисков по методу Монте-Карло [c.255]
Данные формулы остаются в значительной степени справедливыми при любых законах распределения времени обслуживания при наличии простейшего потока отказов. В случае, если последний отличается от простейшего, решение задачи находится путем статистического моделирования процесса (метод Монте-Карло). [c.227]
В этой программе процесс генерации псевдослучайных чисел по отношению к известным методам генерации упрощен. Напомним, что в основе этих методов лежит метод статистических испытаний, или метод Монте-Карло, применение которого обосновывается предельными теоремами теории вероятностей. [c.154]
В процессе реализации метода Монте-Карло производится моделирование случайных событий и соответствующих им случайных величин. При таком моделировании определяется, произошло или не произошло в данном испытании некоторое событие А, вероятность которого известна и равна Р(А), и устанавливается, какое значение приняла соответствующая случайная величина X, закон распределения которой известен. С этой целью решают вспомогательную задачу, состоящую в моделировании равномерно распределенной в интервале (0,1) случайной величины со, Пусть, например, известна вероятность некоторого события А [c.154]
Учитывая матричную форму изложения в учебнике вопросов множественной регрессии, в приложении (главе 11) приведены основные сведения из линейной алгебры. Кроме того, в ыаве 12 рассмотрено применение компьютерных пакетов для оценивания эконометрических моделей, а также проведение эксперимента по методу Монте-Карло, основанного на компьютерном моделировании случайных величин. [c.4]
Однако оказывается, что тест Дики—Фуллера в этом случае неприменим При его использовании гипотеза о нестационарности комбинации будет отвергаться слишком часто. На самом деле критические значения для /-статистики в этом случае другие. Они были оценены методом симуляции (методом Монте-Карло, см. гл. 12). Сравнение наблюдаемого значения Г-статистики с этими уточненными оценками критических зна- [c.221]
Система EXPRESS разработана для принятия управленческих решений и содержит стандартный набор функций финансового планирования и анализа, в том числе, функции по формированию прогнозных финансовых отчетов, бюджетированию, анализу, проектированию, анализу целей и консолидации данных. К специальным функциям системы относится, в частности, анализ рисков (в том числе, моделирование методом Монте-Карло). [c.326]
Имитационное моделирование по методу Монте-Карло (Monte- arlo Simulation) позволяет построить математическую модель для проекта с неопределенными значениями параметров, и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию), получить распределение доходности проекта. Блок-схема, представленная на рис. 7.6, отражает укрупненную схему работы с моделью. [c.242]
Программный пакет Risk-Master позволяет в диалоговом режиме осуществить процедуру подготовки информации к анализу рисков инвестиционного проекта по методу Монте-Карло и провести расчеты. [c.243]
Соболь ИМ. Метод Монте-Карло. — М. Физматгиз, 1968. - 218 с. [c.262]
Смотреть страницы где упоминается термин Метод Монте-Карло
: [c.448] [c.154] [c.219] [c.391] [c.329] [c.257]Смотреть главы в:
Эконометрика -> Метод Монте-Карло
Количественные методы в финансах -> Метод Монте-Карло
Имитационное моделирование экономических процессов -> Метод Монте-Карло
Энциклопедия финансового риск-менеджмента -> Метод Монте-Карло
Введение в экономико-математическое моделирование (1984) -- [ c.155 ]
Эконометрика (2002) -- [ c.285 , c.287 ]
Приближенное решение задач оптимального управления (1978) -- [ c.405 ]
Большая экономическая энциклопедия (2007) -- [ c.178 , c.367 ]
Математические методы моделирования экономических систем Изд2 (2006) -- [ c.118 ]
Опционы полный курс для профессионалов (2003) -- [ c.335 ]
Справочник по математике для экономистов (1987) -- [ c.303 ]
