V) — плотность распределения вероятностей, для размеров месторождений, оставшихся неоткрытыми (по форме совпадает с исходным, [c.83]
Статистическое описание. Эту форму описания риска и неопределенности применяют, когда модель объекта определяется по результатам выборочных экспериментов в условиях действия случайных помех и ошибок. Эта форма тесно связана с предыдущей, но принципиально отличается от нее тем, что в условиях ограниченного эксперимента удается получить лишь выборочные оценки параметров плотности распределения или ее моментов. Таким образом, вместо истинных значений моментов M(Z) и [c.46]
Если приходится иметь дело с вариационным рядом с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала. Полученное отношение называется плотностью распределения [c.99]
Плотность распределения используется как для расчета обобщающих показателей, так и для графического изображения вариационных рядов с неравными интервалами. [c.99]
В интервальном вариационном ряду, тем более при непрерывной вариации признака, строго говоря, каждое значение признака встречается только один раз. Модальным интервалом является интервал с наибольшей частотой. Внутри этого интервала находят условное значение признака, вблизи которого плотность распределения, т.е. число единиц совокупности, приходящееся на единицу измерения варьирующего признака, достигает максимума. Это условное значение и считается точечной модой. Логично предположить, что такая точечная мода располагается ближе к той из границ интервала, за которой частота в соседнем интервале больше частоты в интервале за другой границей модального интервала. Отсюда имеем обычно применяемую формулу (5.15) [c.103]
Наибольшее распространение получили величины, распределенные по нормальному закону или закону Гаусса. Плотность распределения такой величины выражается формулой [c.262]
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение и получения возможности сравнивать частоты. [c.32]
Плотность распределения — это частота, рассчитанная на единицу ширины интервала. Она показывает, сколько единиц в каждой группе приходится на единицу величины интервала. [c.32]
Плотностью вероятности (плотностью распределения или просто плотностью) ф(х) непрерывной случайной величины X называется производная ее функции распределения [c.30]
Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X,Y) называется вторая смешанная частная производная ее функции распределения, т.е. [c.37]
При каком значении параметра С эта функция является плотностью распределения некоторой случайной величины Найти математическое ожидание и дисперсию случайной величины X. [c.49]
A5/S (см. также следующий раздел). Эту характеристику по /-му ресурсу можно задавать величиной Е] — математического ожидания недопоставки АР/Р°. В случае непрерывной функции эластичности ф/ при известной плотности распределения (k.S ISj) случайной величины A5 75j она выражается так [c.29]
Шаги 1 и 2 многократно повторяют, например 1000 раз, и полученные 1 000 значений NPV проекта используют для построения плотности распределения значений чистого приведенного дохода с его математическим ожиданием и стандартным отклонением. [c.244]
В результате анализа, проведенного методом Монте-Карло, эксперт получает значение ожидаемой чистой приведенной стоимости проекта и плотность распределения этой случайной величины. Однако этих данных недостаточно для того, чтобы аналитик установил, действительно ли прибыльность проекта настолько велика, что компенсирует риск по проекту, оцененный стандартным отклонением и коэффициентом вариации. Ряд исследователей избегает использования данного метода ввиду сложности построения вероятностной модели и множества вычислений, однако при корректности модели метод дает весьма надежные результаты, позволяющие судить как о доходности проекта, так и о его устойчивости (чувствительности). [c.252]
Например, если плотность распределения вероятностей будет равномерной функцией в интервале от т(1) до т(2), то расчетное выражение упрощается и будет иметь вид [c.90]
Избыточно закупленный товар приносит дополнительные издержки а(1)руб./т. Дефицит товара влечет потери а(2) руб./т. Требуется определить т — предпочтительный размер закупаемой партии товара, если потребность при розничной реализации является случайной величиной и описывается функцией /(s) — плотностью распределения вероятностей. [c.90]
Нормальный закон распределения имеет две формы представления плотность распределения (рис. 8.1 а) и функцию распределения (рис. 8.1 б). [c.117]
В случае нормальности плотности распределений / (s) [c.204]
| Рис. 4.2.3. Вид плотности распределения для суммы логарифмически нормально распределенных случайных величин | 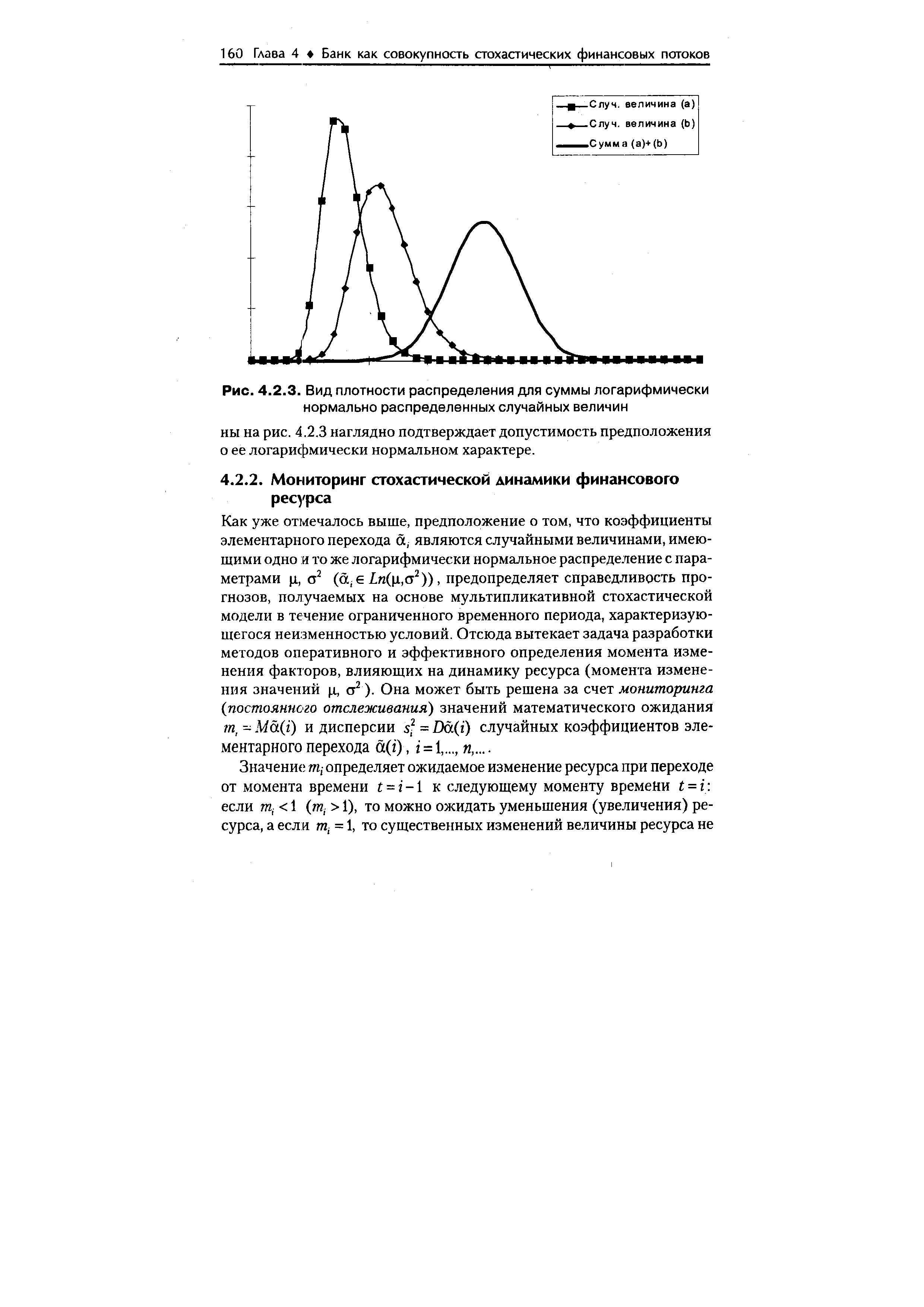 |
В (1) % - среднестатистическая скважность импульсов. шу - среднеквадратическое значение аддитивного Гауссовского шума, л" =о дБм, J > - плотность распределения вероятности 0, Ареал — наблюдаемая амплитуда принимаемого сигнала, А и Е- пороговые амплитуда и энергия, Е (в) - энергия в реальном такте. [c.87]
Принимаем, что плотность распределения смешанных случайных величин стремится к нормальному закону распределения. Предельную точку кривой нормального распределения выражаем через функцию Лапласа [c.91]
Пусть плотность распределения поступления нефтепродукта от НПЗ fk (Qkt) имеет, например, вид представленный на рис. 8, а. Тогда зависимость риска срыва функционирования этого узла Rkt ( ft,) от принимаемых решений, определенного в соответствии с уравнением (4), имеет вид, представленный на рис. 8,6. [c.93]
АППРОКСИМАЦИЯ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ СДАЧИ НЕФТЕПРОДУКТОВ НЕФТЕПЕРЕРАБАТЫВАЮЩИМ ЗАВОДОМ И ПОТРЕБЛЕНИЯ НЕФТЕПРОДУКТОВ [c.257]
Если задана плотность распределения ресурсов f(t), то дисперсия вычисляется аналитически из выражения [c.47]
Для связей характерна разветвленная сеть с параллельным, последовательным и смешанным соединением элементов (действий). Взаимозависимые (последовательная цепь) и взаимовлияющие (параллельная и смешанная цепи) связи, их форма, плотность распределения, активность существенно неодинаковы на разных стадиях процесса бурения скважин и динамического преобразования ЧМС. Производственные операции, приемы и виды реализуемой деятельности, состав и структура вовлеченных в нее функций и свойств человека характеризуются, как видно, большим разнообразием показателей значимости и сложности. Следствием этого является неравномерность распределения производственных несчастных случаев во времени и пространстве, среди профессионалов [c.242]
Пусть далее точное число Л/ объектов в области поиска заранее неизвестно. Предполагается известной лишь производящая функций- соответствующей случайной величины Ц, (z)= 2Lp(N= )i.. Каждый из объектов поиска характеризуется своим 1 —мерным вектором значений параметров X = (X , .,.Х . Априорная информация о, значениях параметров каждого из объектов задается t —мерной плотностью распределения . / °(л L) X Lez j 7 < R г (I - J, < ,.,. N). Пару V/o (2.) ffaj будем называть априорным состоянием природы. [c.79]
Был проведен анализ работы отечественной УЗК на Ново-Уфимском НПЗ для исследования уровня надежности реакторов. Практика показывает, что в современном производственном процессе наиболее слабым (и ответственным) звеном в технологической цепи УЗК являются реакторы. Следует отметить, что особое значение безотказного функционирования реакторов определяется их влиянием на отказ всей системы. Реактор УЗК представляет собой цилиндрический вертикальный пустотелый аппарат, снабженный верхним (полушаровым) и нижним (коническим) днищами с горловинами для ввода гидрорежущего инструмента и выгрузки кокса. Информация об отказах оболочки собрана из ремонтных журналов и дефектных ведомостей по эксплуатации УЗК. Анализ обработки статистической информации показал, что дифференциальная функция плотности распределения отказов реакторов подчиняется закону Вейбула. 1,0 [c.51]
Нами предлагается использовать для всех изделий технологического назначения более универсальный закон распределения — закон Вейбула. Плотность распределения и его функция имеют вид [1] [c.45]
При обработке полупроводниковых структур обнару живается наличие дефектов, вызываемых структурными дефектами в кремниевой пластине, проколами (дефектами) в процессе фотолитографии, и других дефектов в результате многочисленных процессов нанесения сло в, связанных с недостатками технологии, оборудования. В общем случае считают, что все эти дефекты некорре-лированы. Плотность распределения дефектов различна, наименьшая плотность дефектов характерна для центра пластин, по краям плотность дефектов увеличивается. Плотность дефектов состоит из двух составляющих плотности дефектов материалов и плотности технологических дефектов. Достаточно подробно данное явление рассматривается в учебных пособиях и монографиях по технологии интегральных микросхем. Зависимость уровня выхода годных изделий от проколов (дефектов) для стадии обработки пластин имеет вид [c.73]
Асимметрия служит для оценки симметричности распределения случайной величины относительно средней. Если асимметрия — положительное число, распределение имеет сдвиг в сторону положительных значений, иначе — в сторону отрицательных значений. Эксцесс является характеристикой остроконечности или сглаженности кривой распределения плотности вероятности случайной величины. Эксцесс равен нулю для нормального распределения, положителен для остроконечных и отрицателен для сглаженных по сравнению с нормальной плотностью распределения. [c.462]
Использование бейесовского подхода (6.47) требует знания априорных вероятностей и плотностей распределения вероятностей. [c.204]
Предполагается, что поступление нефтепродукта к поставщикам Qftl, потребление нефтепродукта потребителями /< и время движения нефтепродукта Та — величины случайные, а fkt №i) fk2 (Vftz) и fd(Td)—плотности распределения величин [c.88]
Смотреть страницы где упоминается термин Плотность распределения
: [c.152] [c.77] [c.80] [c.82] [c.83] [c.83] [c.44] [c.61] [c.99] [c.99] [c.203] [c.204] [c.19] [c.19]Смотреть главы в:
Практическое руководство по управлению качеством -> Плотность распределения
Математические методы моделирования экономических систем Изд2 (2006) -- [ c.12 ]
Эконометрика начальный курс (2004) -- [ c.510 , c.513 ]
Справочник по математике для экономистов (1987) -- [ c.296 ]
