На левой гистограмме мы делаем предположение, что для предприятия г-жи Хартии Вольнэсти возможны только два исхода - высокий спрос или низкий спрос. На гистограмме показана приведенная стоимость в первом году при допущении, что бизнес не останавливается. Логарифмическое нормальное распределение на правом рисунке более реалистично, поскольку подразумевает бесконечный ряд возможных значений приведенной стоимости и учитывает промежуточные результаты Модель Блэка—Шольца основана на логарифмическом распределении. [c.567]
Гипотеза о логарифмически нормальном распределении коэффициентов элементарного перехода обеспечивает удобство и простоту про- [c.158]
| Рис. 4.2.3. Вид плотности распределения для суммы логарифмически нормально распределенных случайных величин | 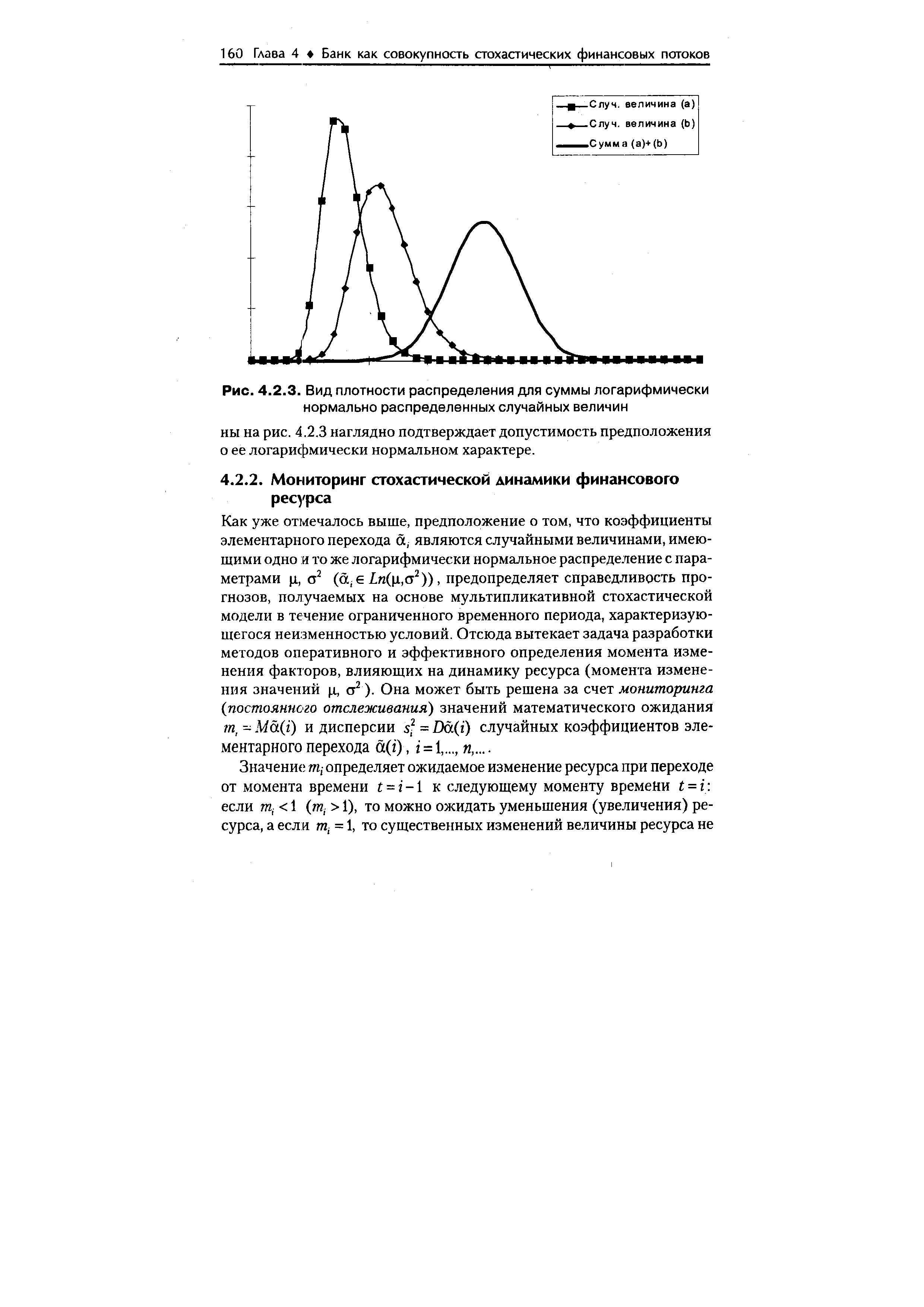 |
Предположим, что случайная величина а имеет логарифмически нормальное распределение (ае 1и( ха,а2)) с математическим ожиданием ц и с дисперсией а2, то есть предположим, что логарифм этой случайной величины имеет нормальное распределение с математическим ожиданием ц и с дисперсией a2 ( In a e N( i, сг2)). Плотность распределения [c.182]
Логарифмически-нормальное распределение. Распределение случайной величины Y называется логарифмически-нормальным, если логарифм этой величины распределяется по нормальному закону [46] [c.26]
Логарифмически нормальное распределение [c.99]
| Рисунок 3-15 Нормальное и логарифмически нормальное распределения | 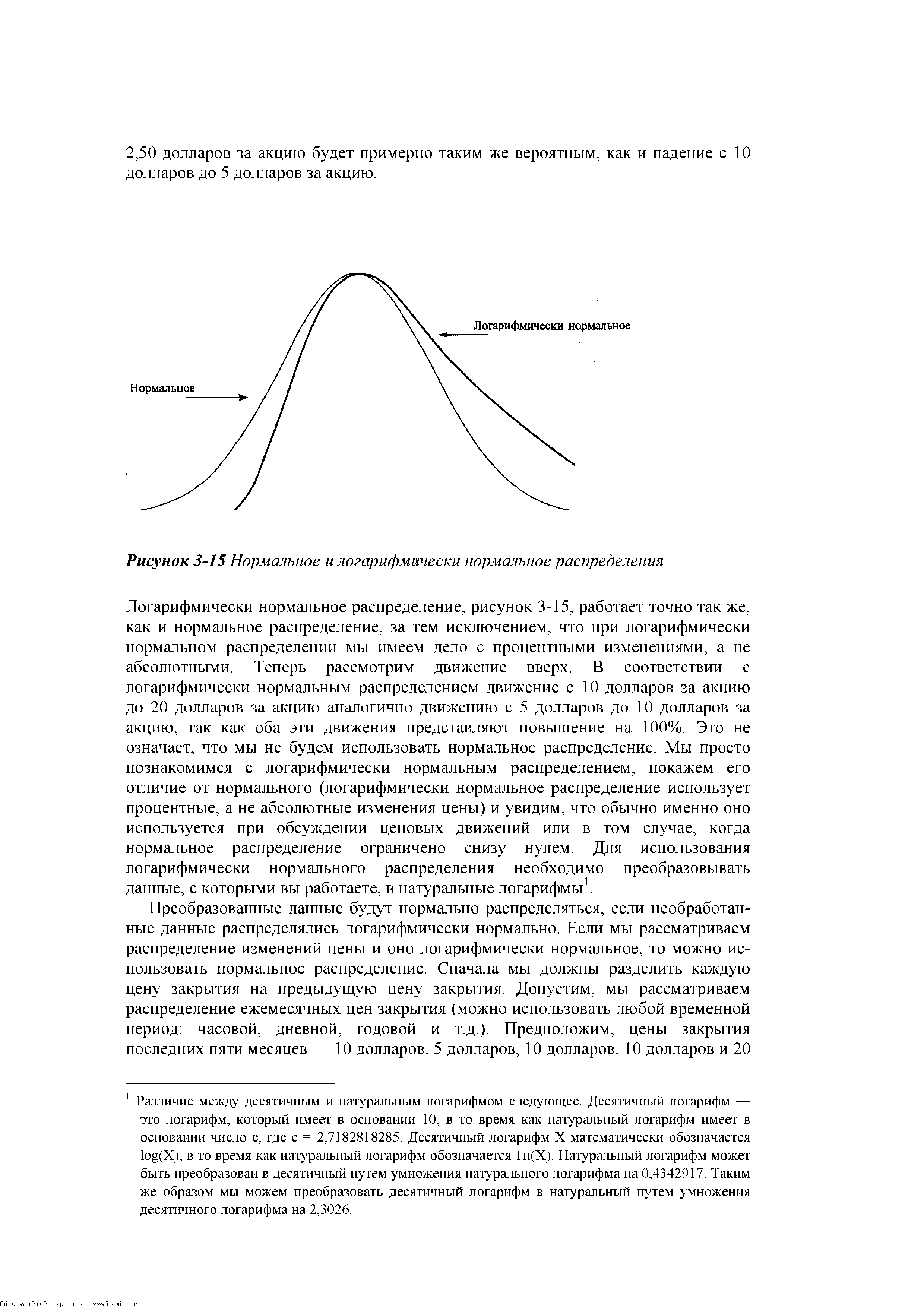 |
Среднедушевой денежный доход в единицу времени (за месяц) рассматривается как случайная величина, имеющая логарифмически нормальное распределение. Это означает, что X = ег, а случайная величина Y, представляющая собой логарифм среднедушевого дохода (Y = InZ), является нормально распределенной случайной величиной. [c.356]
Можно показать, что математическое ожидание случайной величины X, имею-щей логарифмически нормальное распределение, равно Е(Х) = ехр а+ —). Отсюда [c.357]
Распределения вероятностей доходности и доверительные интервалы. Значительная часть данных, используемых в финансовом анализе, имеет нормальное или логарифмически нормальное распределение. Свойства нормального распределения, как было указано ранее, точно определяют связь между величинами интервала, в котором с определенной доверительной вероятностью реализуются исходы событий по получении определенной доходности, и средним квадратическим отклонением. Так, можно утверждать 68,3% всех исходов лежит в пределах одного среднего квадратического отклонения от ожидаемого значения, 99,5% — в пределах двух средних квадратических отклонений и 99,73% — в пределах трех средних квадратических отклонений. Другие [c.61]
Логнормальное, логарифмически-нормальное распределение 176 [c.472]
Весьма часто физические параметры подчиняются так называемому логарифмически нормальному распределению. На основании анализа табл. 95 и 96 можно утверждать, что парные коэффициенты корреляции, подсчитанные по параметрам в логарифмическом масштабе, будут незначимо отличаться от линейных парных коэффициентов корреляции. В табл. 95 и 96 приведены парные коэффициенты корреляции в линейном (верхняя строка) и логарифмическом (нижняя строка) масштабах. Незначимым различие считается, если доверительные интервалы для парных коэффициентов корреляции пересекаются. Рамкой обведены те клетки, в которых различие парных коэффициентов корреляции оказалось значимым. Как видно, для всех приборов существенно нелинейна взаимосвязь 1-го и 6-го, 2-го и 6-го, 2-го и 5-го параметров. Для годных приборов то же относится к взаимосвязи 1-го и 6-го, 2-го и 6-го параметров. [c.189]
К математическим средствам оценки рисков относятся статистические расчеты, нормальное распределение, логарифмически нормальное распределение, линейное программирование, эконометрические методы и т.д. [c.734]
ГОСТ 11.009—79 Система управления качеством продукции. Прикладная статистика. Правила определения оценок и доверительных границ для параметров логарифмически нормального распределения . [c.26]
Стандарт устанавливает правила определения оценок и доверительных границ для параметров логарифмически нормального распределения по совокупности статистических данных, если эти данные подчинены логарифмически нормальному распределению. [c.26]
Стандарт содержит общие положения оценки параметров а и о определение доверительных границ для параметров а и а и т. д. Приведены примеры применения правил стандарта способ нахождения оценки параметра а через размах, а также оценки для математического ожидания и дисперсии логарифмически нормального распределения доверительные границы для математического ожидания теоретические основы стандарта. [c.26]
| Рис. 12.4. Логарифмически нормальное распределение с разными | 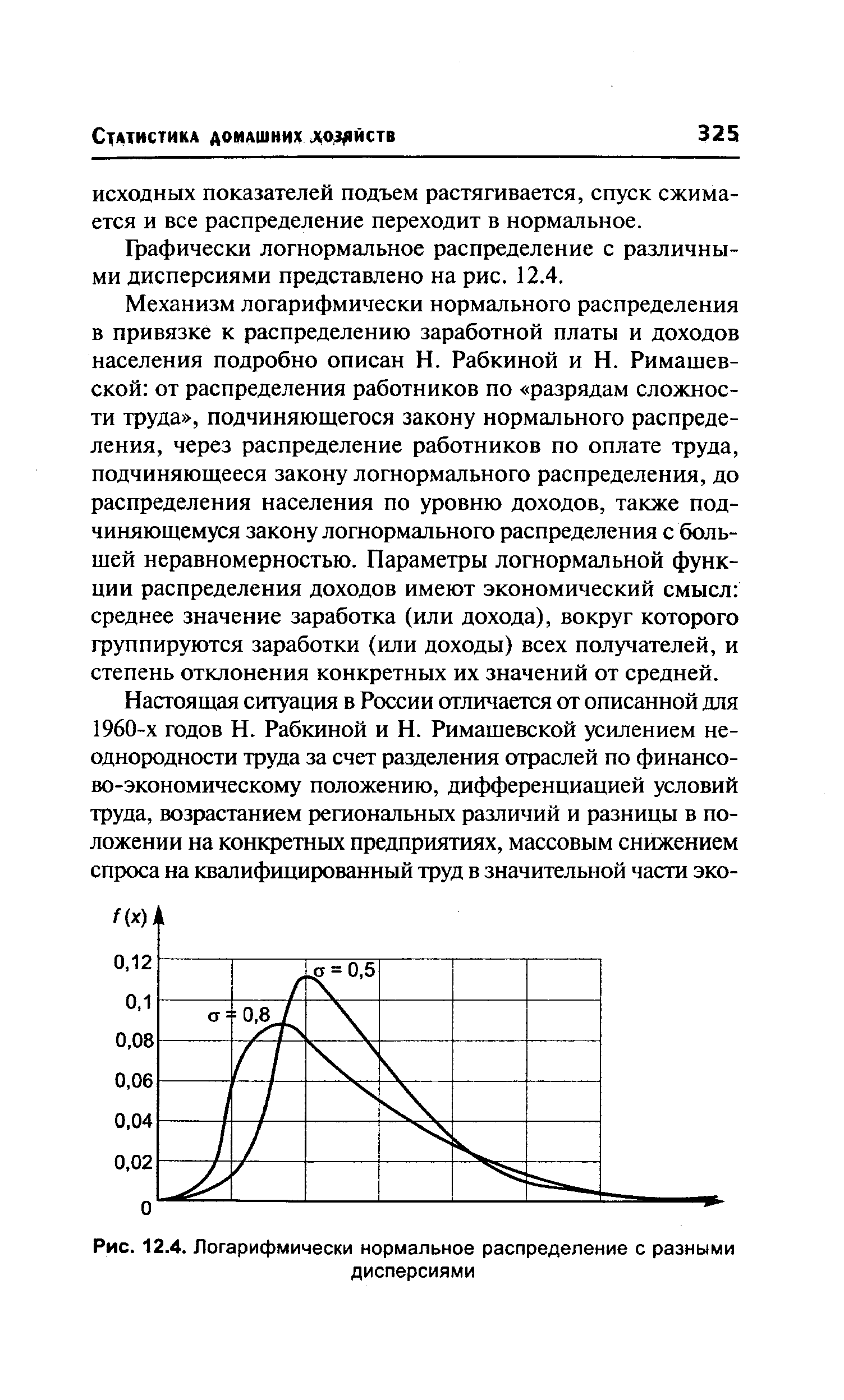 |
Логарифмически нормальное распределение возникает в ситуации, когда исследуемая случайная величина формируется под воздействием большого числа мультипликативных случайных факторов. Можно показать, что [c.520]
В случае курсов акций диапазон значений может быть смоделирован как процесс с логарифмически нормальным распределением. Следующая проблема состоит в том, что решения относительно базисного актива или проекта, вероятно, придется принимать непрерывно или цена основной акции может непрерывно эволюционировать, причем не только в дискретных стадиях. Как отмечалось выше, дискретные стадии с различным риском требуют различных ставок дисконта. Если предположить непрерывность процесса и, соответственно, непрерывность множества возможных решений, то возникает бесконечное множество стадий. Таким образом, ставка дисконта теперь также непрерывно колеблется, изменяясь во времени вместе со стоимостью соответствующего актива. Следующая классическая формула, известная как модель Блэка-Шольца, дает цену европейского колл опциона для случая непрерывного времени [c.178]
С помощью этой модификации нормальное распределение преобразуется в логарифмически нормальное распределение. Цена любого свободно котируемого инструмента имеет нулевое значение в качестве нижнего предела1. Поэтому когда цена этого инструмента падает и приближается к нулю, то, теоретически, цене инструмента должно быть все труднее понизиться. Рассмотрим некую акцию стоимостью 10 долларов. Если бы акция упала на 5 долларов до 5 долларов за акцию (50% понижение), то в соответствии с нормальным распределением она может также легко упасть с 5 долларов до 0 долларов. Однако при логарифмически нормальном распределении подобное падение на 50% с цены в 5 долларов за акцию до цены [c.100]
Логарифмически нормальное распределение, рисунок 3-15, работает точно так же, как и нормальное распределение, за тем исключением, что при логарифмически нормальном распределении мы имеем дело с процентными изменениями, а не абсолютными. Теперь рассмотрим движение вверх. В соответствии с логарифмически нормальным распределением движение с 10 долларов за акцию до 20 долларов за акцию аналогично движению с 5 долларов до 10 долларов за акцию, так как оба эти движения представляют повышение на 100%. Это не означает, что мы не будем использовать нормальное распределение. Мы просто познакомимся с логарифмически нормальным распределением, покажем его отличие от нормального (логарифмически нормальное распределение использует процентные, а не абсолютные изменения цены) и увидим, что обычно именно оно используется при обсуждении ценовых движений или в том случае, когда нормальное распределение ограничено снизу нулем. Для использования логарифмически нормального распределения необходимо преобразовывать данные, с которыми вы работаете, в натуральные логарифмы1. [c.101]
Мы немного познакомились с математикой нормального и логарифмически нормального распределения и теперь посмотрим, как находить оптимальное f по нормально распределенным результатам. Формула Келли является примером параметрического оптимального f, где f является функцией двух параметров. В формуле Келли вводные параметры — это процент выигрышных ставок и отношение выигрыша к проигрышу. Однако формула Келли даст вам оптимальное f только тогда, когда возможные результаты имеют бернуллиево распределение. Другими словами, формула Келли даст правильное оптимальное f, когда есть только два возможных результата, в противном случае, как, например, в нормально распределенных результатах, формула Келли не даст вам правильное оптимальное f2. [c.102]
Логарифмически нормальное распределение зависит от двух параметров математического ожидания а и среднего квадратичес-кого отклонения о случайной величины Y (логарифмов доходов) а = E(Y) = E(InX), а2 = var(F) = var(hiA). Расчет второго параметра проводится на основе данных выборочного бюджетного обследования по следующей формуле [c.357]
Для изучения особенностей дифференциации населения по уровню доходов используются структурные характеристики радов распределения, такие, как мода, медиана, квартили, децили и др. Эти статистические характеристики могут быть выражены и исчислены через параметры логарифмически нормального распределения (а и о). Вместе с тем приближенную оценку структурных характеристик можно получить и на основе уже построенных статистических рядов, публикуемых органами государственной статистики. [c.358]
ЛОГНОРМАЛЬНОЕ, ЛОГАРИФМИЧЕСКИ-НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ [log-normal distribution] — распределение случайной величины, логарифм которой характеризуется нормальным распределением. С его помощью удобно описывать некоторые экономические явления, напр., дифференциацию заработной платы, распределение доходов. [c.176]
При использовании вероятностных моделей риска распространены два характерных заблуждения. Во-первых, если величина ущерба зависит от множества причин, то она должна иметь нормальное распределение. Это ошибочное мнение, так как все зависит от способа их взаимодействия. Если причины действуют аддитивно (суммарно), то согласно Центральной предельной теореме теории вероятностей величина ущерба действительно имеет приблизительно нормальное (гауссово) распределение. Если же причины действуют мультипликативно, то в силу той же теоремы следует приближать распределение величины ущерба X с помощью логарифмически нормального распределения. Если же основное влияние оказывает слабое звено , то согласно теоремам, доказанным академиком Б. В. Гнеденко, величину ущерба Xследует описывать с помощью распределения из семейства Вейбулла—Гнеденко. [c.276]
Предположение о нормальном или логарифмически-нормальном распределении запасов месторождения. В зависимости от объема запасов и типа нефтеносного пласта возможно сильно выраженное логарифмически-нормальное распределение. Однако в зависимости от типа пласта оно может быть и нормальным. Нормальное распределение легче поддается оценке, а логарифми- [c.161]
Когда а < 2 и (3 = 0, оба хвоста следуют закону Парето. Как мы говорили ранее, Парето (Pareto, 1897) нашел, что логарифмическое нормальное распределение не описывало частоту уровней дохода у верхних 3 процентов населения. Вместо этого хвосты становились все более и более длинными, так что [c.199]
Помимо гауссового распределения в аналитике, особенно при определении следовых количеств, некоторую роль играет и логарифмическое нормальное распределение. Асимметрия этого распределения вносит две особенности [c.41]
Механизм логарифмически нормального распределения в привязке к распределению заработной платы и доходов населения подробно описан Н. Рабкиной и Н. Римашев-ской от распределения работников по разрядам сложности труда , подчиняющегося закону нормального распределения, через распределение работников по оплате труда, подчиняющееся закону логнормального распределения, до распределения населения по уровню доходов, также подчиняющемуся закону логнормального распределения с большей неравномерностью. Параметры логнормальной функции распределения доходов имеют экономический смысл среднее значение заработка (или дохода), вокруг которого группируются заработки (или доходы) всех получателей, и степень отклонения конкретных их значений от средней. [c.325]
Предположим, что все случайные коэффициенты элементарных переходов независимы, и каждый из этих коэффициентов имеет логарифмически нормальное распределение. Последнее будем обозначать а,, е 1я(ц,,а2), где ц., а2 — параметры логарифмически нормально распределенной случайной величины а,-. Иными словами, предполагается, что натуральный логарифм Ina, случайной величины а, имеет нормальное распределение с математическим ожиданием М1па,=ц, и с дисперсией Dlna, = о2 (Ina,.e JV(n,,а2)). Знание плотности распределения [c.153]
