Нормальное распределение случайной величины [c.59]
В других случаях сами величины Y или X могут не иметь нормального распределения, но некоторые функции от них распределены нормально. Например, известно, что логарифм доходов населения — нормально распределенная случайная величина. Вполне естественно считать нормально распределенной случайной величиной пробег автомобиля. Часто гипотеза о нормальном распределении принимается во многих случаях, когда нет явного ей противоречия, и, как показывает практика, подобная предпосылка оказывается вполне разумной. [c.18]
Из формул (2.34), (2.36) следует, что линии регрессии Му (X) и MX(Y) нормально распределенных случайных величин представляют собой прямые линии, т. е. нормальные регрессии Y по X и X по Y всегда линейны. [c.40]
Для нормально распределенных случайных величин термины некоррелированность и независимость равносильны. [c.40]
Возмущение е, (или зависимая переменная у,) есть нормально распределенная случайная величина. [c.61]
Полагая выполнение предпосылки 5 (с. 61) регрессионного анализа, т. е. нормальную классическую регрессионную модель (3.22), будем рассматривать значения у/ как независимые нормально распределенные случайные величины с математическим ожиданием М(у,-)=р0+Р,, -, являющимся функцией от х и постоянной дисперсией ст2. [c.63]
Следовательно, плотность нормально распределенной случайной величины у [c.63]
В этом случае гипотеза о гомоскедастичности будет равносильна тому, что значения е, ..., ет и en-m+i,..., е (т. е. остатки е, регрессии первых и последних т наблюдений) представляют собой выборочные наблюдения нормально распределенных случайных величин, имеющих одинаковые дисперсии. [c.159]
Пусть в этой двойственной задаче t-ro этапа планового периода элементы матрицы А (и ) и составляющие вектора 6f( of) являются независимыми друг от друга нормально распределенными случайными величинами [c.82]
Регрессионный анализ - один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регрессионного анализа необходимо выполнение ряда специальных требований (в частности, х[,х2,...,хп у должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. Зависимости в экономике могут быть не только прямыми, но и обратными и нелинейными. Регрессионная модель может быть построена при наличии любой зависимости, однако в многофакторном анализе используют только линейные модели вида [c.101]
| Рис. 4.2.3. Вид плотности распределения для суммы логарифмически нормально распределенных случайных величин | 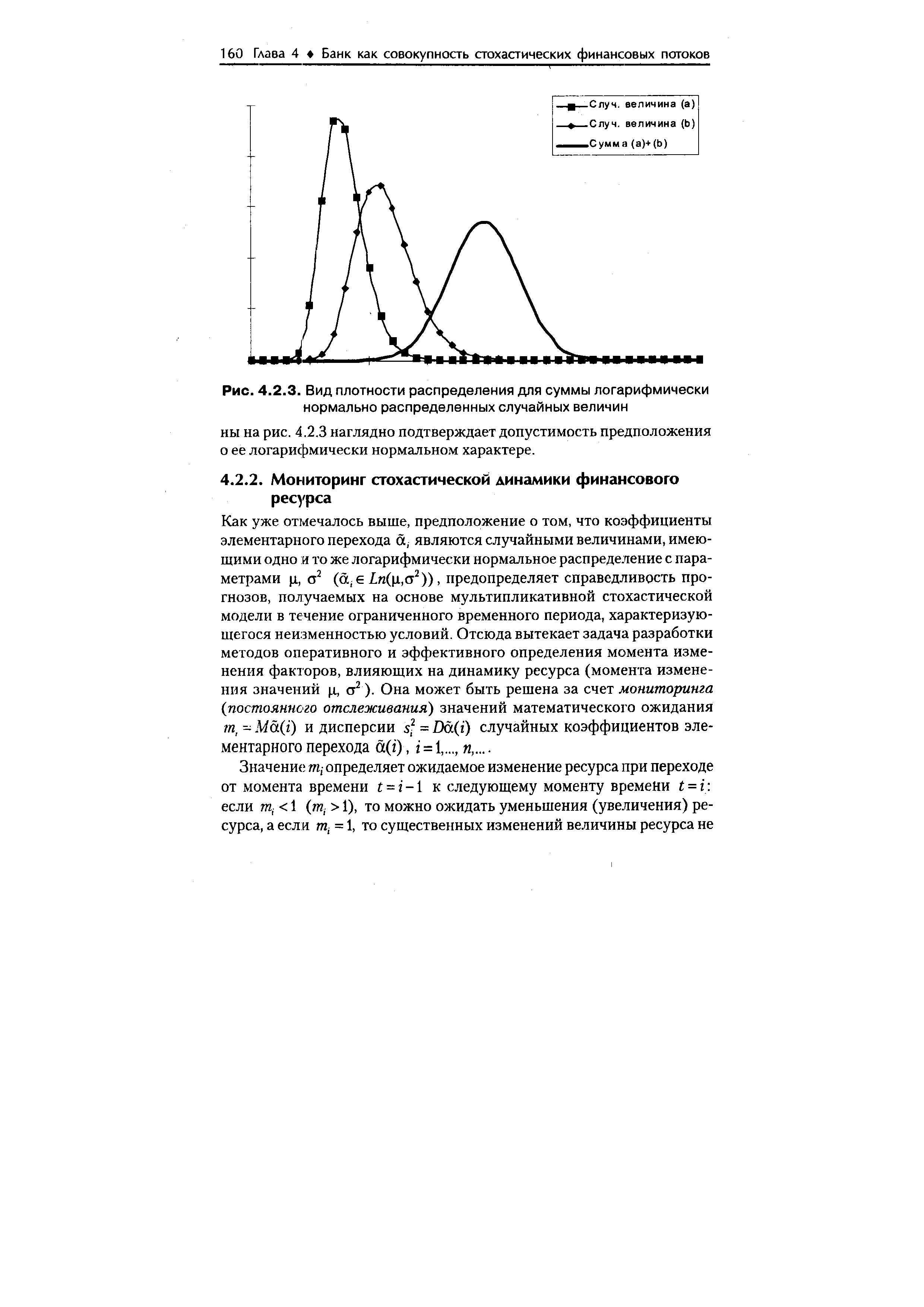 |
Для приведения нормально распределенной случайной величины к стандартному виду, то есть для вычисления z = (х - //)/сг используется функция [c.36]
Пусть х - нормально распределенная случайная величина с плотностью распределения [c.37]
Например, мы знаем, что центрированная нормально распределенная случайная величина с вероятностью 0,9772 не превышает двух стандартных отклонений, а с вероятностью 0,9986 — трех стандартных отклонений. Если один из сценариев спектра состоит в том, что нормально распределенная случайная величина попадает в пределы от +2 до +3 стандартных отклонений, то мы знаем, что вероятность этого сценария равна 0,0214 (0,9986 -0,9772). Значит, мы можем определять совместные вероятности для непрерывных распределений. Кроме того, мы можем сделать сценарий таким маленьким, как нам нужно. В упомянутом ранее примере мы можем использовать сценарий, который состоит в том, что нормально распределенная случайная величина попадает в пределы от +2 до +2,1 стандартных отклонений, или между +2 и +2,000001 стандартных отклонений. [c.164]
Можно попытаться изобразить модель ценообразования как график нормального распределения случайных величин (см. рис. 2-2). В диапазоне вершины находятся допустимые, или оптимальные, значения, а правый и левый края графика представляют собой две крайности одного явления. Крайности практически без споров признаются всеми как недопустимые или плохие состояния, когда есть возможность сравнить их с идеальным состоянием. Идеальное же состояние точно определить нельзя, ибо существует достаточно широкий диапазон допустимых значений. Именно в его пределах и ведутся основные споры о том, хорошо то или иное состояние или плохо. Если принять существование диапазона идеальных значений, то становится понятным, что такие споры бессмысленны, поскольку все эти состояния являются допустимыми. [c.9]
Среднедушевой денежный доход в единицу времени (за месяц) рассматривается как случайная величина, имеющая логарифмически нормальное распределение. Это означает, что X = ег, а случайная величина Y, представляющая собой логарифм среднедушевого дохода (Y = InZ), является нормально распределенной случайной величиной. [c.356]
Для нормально распределенной случайной величины с мате- [c.59]
Если Ek> О, то кривая островершинная, при Ek <0 — плосковершинная (пологая). Метод моментов, как правило, приводит к состоятельным оценкам. Однако при малых выборках оценки могут оказаться значительно смещенными и малоэффективными. Метод моментов достаточно эффективен для оценки параметров нормально распределенных случайных величин. [c.48]
Для оценки величины рассеивания средних выборочных относительно математического ожидания генеральной совокупности в случае нормального распределения случайной величины х можно применить формулу [c.49]
Для нормально распределенной случайной величины доверительный интервал определяется по формулам [c.54]
При проверке гипотез о равенстве средних вначале необходимо проверить гипотезу о независимости одинаково нормально распределенных случайных величин в выборке (х,, х2,..., xt) при неизвестных параметрах М(х) и Дх). Выборку записывают в том же порядке, в каком записывались результаты наблюдений, например, (42, 63, 23, 47, 52, 98, 97, 73, 85, 88). По имеющейся выборке вычисляем D(x) двумя способами [c.60]
Наиболее часто используемой функцией является гауссовское или нормальное распределение. В каноническом виде нормальное распределение случайной величины х записывается следующим образом [c.92]
Подобно функции Лапласа уравнение (2.8) представляет собой квантиль-ное распределение энтропии нормированной нормально распределенной случайной величины на любом отрезке числовой оси. [c.24]
Рассмотрим случай нормально распределенной случайной величины. Из формул (2.5) и (2.6) вытекает, что оценка S(x) среднего квадратического отклонения ст(х) может быть получена так [c.41]
Проведенные эксперименты позволяют сделать выводы о том, что оценка с.к.0., определяемая формулой (2.33) для нормально распределенной случайной величины, не только не уступает по точности, но и в большинстве случаев превосходит оценку Sk, получаемую с помощью формулы (2.32). Причем, как для фиксированного k, так и для k, рекомендуемого для определения закона распределения случайной величины по выборочным данным информационным методом. Во всех случаях обе оценки не выходят за пределы доверительных интервалов, что позволяет рекомендовать формулу (2.32) для практического применения. [c.43]
Вероятность попадания нормально распределенной случайной величины на участок от L до определяется общей формулой [c.136]
Предполагая, что параметры dij, 5ц, k j независимые между собой нормально распределенные случайные величины, можно в соответствии с указаниями 1 гл. 3 записать следующий детерминированный эквивалент стохастической задачи планирования угледобычи [c.33]
Откажемся теперь от требования детерминированности матрицы А. Пусть элементы матрицы Л и составляющие вектора b — независимые между собой нормально распределенные случайные величины. [c.66]
Случайные величины как линейные комбинации нормально распределенных случайных величин распределены нормально. Поэтому соотношения (1.5) эквивалентны неравенствам [c.86]
Будем рассматривать только задачи, в которых г распределена нормально. К ним относятся, в частности, задачи вида (1.16) — (1.18), у которых компоненты Ьг вектора b образуют систему нормально распределенных случайных величин, а вектор с детерминирован. Легко видеть, что [c.87]
Диаметр детали, обрабатываемой на токарном станке, вообще говоря, случайная величина. При определенных условиях механизм возникновения случайных отклонений размеров деталей от заданных позволяет в первом приближении считать диаметр /-и детали нормально распределенной случайной величиной Xj N ( j,j, aj). Дисперсия ст2 отклонения размеров деталей от заданных зависит от различных параметров, определяющих режим работы станка. Вид зависимости предполагается известным. Деталь, прошедшая технический контроль, идет в продажу по цене j за штуку (/-го типа), если ее диаметр не выходит из допустимого интервала di x d . Если диаметр детали /-го типа меньше d деталь признается негодной. Если диаметр превышает величину d j, деталь поступает на доработку, и, следовательно, затраты на ее выпуск повышаются. Ясно, что выбор параметров режима станка, гарантирующего максимальное значение средней прибыли при заданных ресурсах и фиксированной вероятности удовлетворения спроса на детали всех типов, сводится к решению задачи стохастического программирования с вероятностными ограничениями. Решение задачи (размеры диаметров деталей) целесообразно определять в виде нормального решающего распределения, статистические характеристики которого зависят известным образом от искомых значений параметров режима работы станка. [c.142]
Регрессионный анализ — один из наиболее разработанных методов математической статистики. Строго говоря, для реализации регресси-онногс анализа необходимо выполнение ряда специальных требований (в частности, Х1,Х2,...х , у должны быть независимыми, нормально распределенными случайными величинами с постоянными дисперсиями). В реальной жизни строгое соответствие требованиям регрессионного и корреляционного анализа встречается очень редко, однако оба эти метода весьма распространены в экономических исследованиях. [c.122]
Тест Голдфелда—Квандта. Этот тест применяется в том случае, если ошибки регрессии можно считать нормально распределенными случайными величинами. [c.159]
Предполагая, что ошибки регрессии представляют собой нормально распределенные случайные величины, проверить гипотезу о гомоскедастичности, используя тест Голдфедда— Квандта. [c.188]
Основное преимущество постановки (3.74) -(3.79) заключается в том, что в главной задаче (3.74) случайным является только вектор ограничений о= Ьг- , а варьируемые векторы условий фиксированы на некотором номинальном уровне R° и R . При этих условиях и нормальном распределении случайных величин ЬДсо) детерминированный аналог главной задачи (3.74), построенный по аналогии с рассмотренным в [47] случаем, будет иметь линейный вид. [c.72]
Согласно теореме Муавра — Лапласа биномиальное распределение стремится к нормальному с ростом объема выборки п. Была выдвинута гипотеза о нормальности распределения случайной величины Дх, которая проверялась методом имитационного моделирования. Для проверки гипотезы использовался критерий согласия Колмогорова. [c.58]
Запись OfjG (a ji al bi N(Bt,b2t) означает, что ац (соответственно bi) — нормально распределенная случайная величина с математическим ожиданием а (соответственно Ij) и дисперсией а (соответст- [c.66]
Смотреть страницы где упоминается термин Нормальное распределение случайной величины
: [c.182] [c.286] [c.287] [c.288] [c.301] [c.82] [c.27] [c.89] [c.60] [c.128] [c.419] [c.434]Смотреть главы в:
Теория экономического анализа -> Нормальное распределение случайной величины
