Итак, здесь RI выше, чем в случае, если система не покупается. Положительное решение, принятое на основании этого критерия, согласуется с решением, принятым по критерию NPV. (Отметим, что увеличение чистого годового денежного потока увеличивает и чистую приведенную стоимость, вычисленную в табл. 15.1.) [c.741]
В последнем разделе мы измеряли риск для одного инвестиционного предложения. Могут иметь место составные инвестиционные проекты. В этом случае существует комбинированный риск и методика измерения риска отличается от той, что использовалась для одного проекта. Метод, который мы будем использовать, напоминает портфельный метод в анализе ценных бумаг. Теория портфеля была рассмотрена в гл. 5 здесь мы применим данный метод к проектам капиталовложений. Ограничения и условия, при которых используется этот метод, будут обсуждены в гл. 15, где мы рассмотрим критерий согласия для рисковых инвестиций. Наша цель здесь — только показать, как измеряется риск для комбинаций рисковых инвестиций, допуская, что такой критерий необходим. [c.398]
Следующий этап связан с использованием высших производных (формула Тейлора), и завершается этот этап обзором метода в целом.Далее рассматриваются некоторые вопросы численной характеристики функций — численных методов (приложение дифференциального исчисления к приближенным вычислениям). На этом этапе устанавливается погрешность уклонения ломаных из секущих, ломаной из касательной, кусочных кривых из парабол Тейлора более высоких степеней от данной функции в зависимости от ее дифференциальных свойств, и сравнивается погрешность. Для простоты рассматривается случай равноотстоящих узлов. Тем самым, устанавливаются границы применимости метода дифференциального исчисления. В качестве дальнейшего развития этого этапа можно рассматривать и другие приближающие модели, конструирование их, руководствуясь, например, следующей схемой 1.Какие узлы мы мы будем использовать 2. Какой класс приближающих функции будем использовать 3. Какой критерий согласия мы применим 4. Какую точность мы хотим [c.12]
В данном анализе при оценке степени согласованности эмпирического и теоретического распределения использовался основанный на критерии Пирсона критерий согласия В. И. Романовского [c.190]
Результаты расчетов параметров кривых распределения приведены в табл. 10. Расчетные частоты вычислялись по формулам 10, 11, 12. Объективной оценкой степени совпадения эмпирических и теоретических частостей является критерий согласия (в данном исследовании использовался критерий согласия В. И. Романовского [47, 88]). Проверка показала, что исследуемые эмпирические интервальные ряды распределения времени пролеживания предметов труда в переходящих заделах достаточно точно описываются найденными кривыми функции плотности р (х). [c.78]
Число единиц в выборке, N Величина интервала, Н Показатель асимметрии ряда, гл Показатель эксцесса, Ех Дисперсия, а Среднее значение, X Критерий согласия, К [c.81]
Полученное эмпирическое распределение будет аппроксимировано непрерывной аналитической функцией, то есть будет идентифицирован закон распределения случайной величины. Также рассмотрено использование критериев согласия при идентификации закона распределения. [c.79]
Использование критериев согласия при идентификации закона распределения случайной величины. [c.87]
После построения гистограммы распределения можно выдвинуть гипотезу о том, что данная гистограмма может быть аппроксимирована одним из изученных ранее законов распределения. При этом степень близости гистограммы и принятой аналитической модели может быть проверена с использованием критериев согласия. Здесь будет рассмотрен один из этих критериев - критерий Пирсона. [c.87]
При использовании критерия согласия Пирсона необходимо вычислить величину [c.87]
Следует особо подчеркнуть, что при проверке модели по критерию согласия определенным является лишь отрицательный ответ, то есть отклонение модели. [c.88]
Положительный ответ означает лишь то, что модель не противоречит эмпирическим данным. Это вовсе не означает, что именно этой моделью данные описываются на самом деле, что это наилучшая модель, что нельзя подобрать другую модель для описания данных и т.д. Фактически, положительный ответ при проверке по критерию согласия следует понимать как "возможно эти данные описываются такой-то моделью", и не более того. [c.88]
Полученная гистограмма проверяется на соответствие нормальному распределению с помощью критерия согласия Пирсона. [c.123]
| Таблица 6.4. Критерии согласия для выходов регрессии и сети | 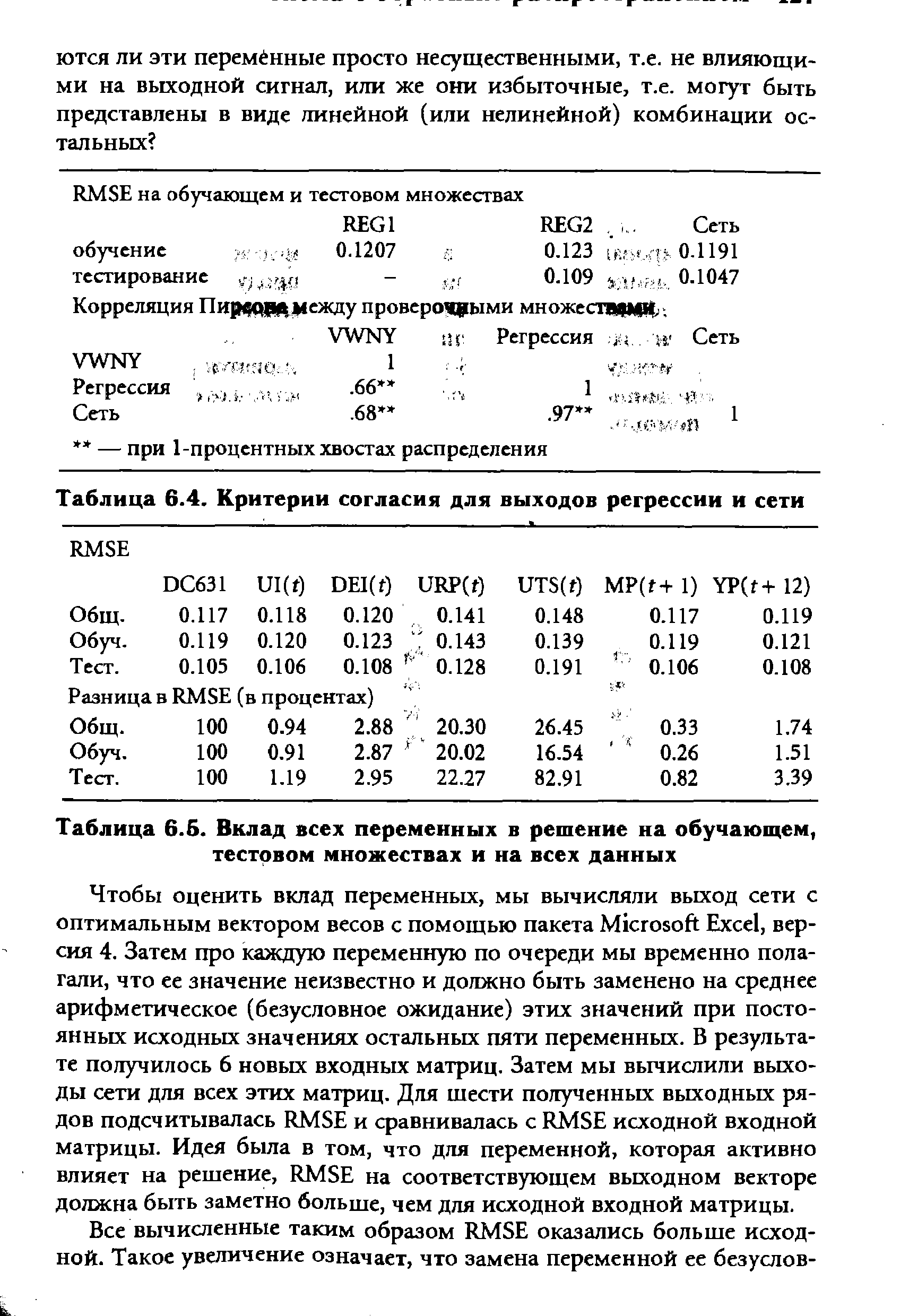 |
По данным задачи 21 проведите выравнивание ряда распределения населения по размеру среднедушевых денежных доходов по кривой нормального распределения. Постройте графики эмпирического и теоретического распределений. Оцените близость эмпирического и теоретического распределений, используя критерии согласия [Пирсона (хи-квадрат), Колмогорова или др.] [c.373]
Т-распределение Стьюдента относится к критериям согласия и основано на использовании средних [c.119]
Независимо от вида используемого критерия согласия в про- [c.68]
Оценка значимости коэффициента конкордации производится по критерию согласия х2 ( хи-квадрат ), который подчиняется распределению с числом степени свободы п - 1. В нашем примере число степени свободы равно /1-1=6-1=5. [c.125]
Для С.п.г. используются разные критерии. В частности, когда проверяется согласие между выборочным и гипотетическим распределениями, используется критерий согласия, напр., т.н. критерий Пирсона "хи-квадрат". См. также Ошибка. [c.344]
При определении закона распределения обратимся к критерию, при помощи которого проверяют, удовлетворяет ли рассматриваемая случайная величина X заданному закону распределения F0(x), - критерию согласия. Критерий согласия %г служит для проверки гипотезы о том, что Fx(x)-F0(x), где Fx(x) - функция распределения X, a Fa(x) - заданное (гипотетическое) распределение. [c.99]
При генерировании случайных величин по нормальному закону с параметрами N(0,1) семь интервалов будут соответствовать примерному соотношению Дх = ст. В этом случае эмпирическая энтропия стремится к постоянному числу Я = 1п- /2ле, что уменьшает погрешности дискретизации непрерывного распределения. Проверка гипотезы проводилась с помощью критериев согласия Пирсона и Колмогорова-Смирнова. При проверке по Х2-критерию вычислялась критическая статистика [c.21]
Заменяя в формуле (2.15) М[Н(х) и D[H(x)] уравнениями (2.3), выводим окончательную формулу информационного критерия согласия [c.29]
В табл. 2.3 приведены значения энтропийных параметров наиболее часто встречающихся в технических приложениях законов распределения. Таблица энтропийных параметров различных законов распределения предоставляет возможность при применении информационного критерия согласия проверить одновременно несколько гипотез, что по существующим методикам сделать без дополнительных расчетов нельзя. [c.29]
Поскольку наиболее распространенным является критерий согласия Пирсона, проведем сравнение информационного критерия J с критерием %2. [c.33]
При выравнивании эмпирического распределения нулевая гипотеза принимается, если при применении информационного критерия согласия [c.33]
Центральная задача математической статистики — определение вида закона распределения генеральной совокупности по выборке из нее. Методика определения во многом зависит от применяемого критерия согласия. Принимая во внимание возможность использования информационного метода определения закона распределения, выберем в качестве критерия оптимизации числа интервалов информационный критерий согласия. В качестве метода исследования используем вновь метод статистических испытаний. [c.38]
ГОСТ 8.532-85 предлагает с помощью критериев согласия не менее чем при 10 %-ном уровне значимости при и>50 и при 15 < п < 50 (для нормального распределения - с помощью критерия Вилкоксона для разностей пар - для проверки симметричности распределения) относить массив результатов аттестации СО к одному из классов распределений нормальному, симметричному, несимметричному. Для каждого класса распределений значения основных метрологических характеристик СО определяют различными способами. [c.30]
При решении задач (3) (5) и (4) (5), которые представляют собой две классические однокритериальные задачи линейного программирования, получаем крайне противоречивые результаты. В первом случае цена Ц равна нулю, а доля накладных расходов вуза л стремится к максимуму и превышает 100 %. Во втором случае получаем обратную ситуацию, когда Ц достигает своего максимального уровня, а А. рана нулю. Таким образом, можно сделать вывод, что критерии А, и Ц являются крайне противоречивыми. В связи с этим необходимо найти некое компромиссное решение. Компромисс в этом случае будет заключаться в том, что мы ослабляем требования по каждому критерию и вводим критерий согласия, обозначив его через переменную j.. Максимальное значение критерия согласия равно 1 [2]. [c.26]
Для определения степени согласованности эмпирического и теоретического распределений предложены различные критерии согласия. Так, известны критерий согласия Пирсона, Романовского, Колмогорова, Ястремского. Критерий согласия Пирсона сводится к исчислению по распределению Пирсона вероятности достижения л 2 данного значения Р = х2. При этом х2 рассчитывается по формуле (9.3) [c.189]
Оценка качества модели обычно основывается на критерии согласия типа средней квадратичной ошибки (MSE) или квадратного корня из нее (RMSE). Эти критерии показывают, насколько предсказанные значения оказались близки к обучающему, подтверждающему или тестовому множествам. Для рядов с большим разбросом Лапедес [171] предложил критерий средней относительной вариации [c.62]
Самый распространенный метод выбора нейронно- сетевой модели с наилучшим обобщением — это проверка критерия согласия (MSE, ARV и др.) на тестовом множестве, которое не использовалось при обучении. Если же данных мало, разбивать их на обучающее и подтверждающее множество нужно разными способами. Такое перекрестное подтверждение может потребовать много времени, особенно для нейронных сетей с их длительным процессом обучения. [c.65]
В линейном анализе временных рядов можно получить несмещенную оценку способности к обобщению, исследуя результаты работы на обучающем множестве (MSE), число свободных параметров (W) и объем обучающего множества (N). Оценки такого типа называются информационными критериями (1 ) и включают в себя компоненту, соответствующую критерию согласия, и компоненту штрафа, которая учитывает сложность модели. Барроном [30] были предложены следующие информационные критерии нормализованный 1 Акаике (NAI ), нормализованный байесовский 1 (NBI ) и итоговая ошибка прогноза (FPE) [c.65]
В отсутствие каких-либо готовых схем для оптимального выбора модели исследователь должен опробовать различные статистические критерии согласия. Так, Утанс и Муди [270] оценивали риск предсказания, полученный при различных архитектурах сети, а Каяма и др. [157] находили общее число дублирующих друг друга элементов в скрытом слое. Мы же просто сравнивали величины квадратного корня из среднеквадратичной ошибки (RMSE) на тестовом множестве, состоящем из 60 наблюдений, относящихся к последним 5 годам интервала наблюдений (1981-85 гг.). Для дальнейшей работы была взята та архитектура сети, которая давала наименьшее RMSE. [c.140]
Эти критерии согласия позволяют провести проверку гипоте- [c.68]
При оценивании энтропии н.с.в. встает вопрос о выборе количества интервалов разбиения экспериментальных данных. Эта задача аналогична типичным задачам математической статистики определение закона распределения, расчет оценок эмпирических распределений, вычисление критериев согласия. А. Хальд [101] показал, что существует оптимальное число интервалов группирования, когда ступенчатая огибающая гистограмма наиболее близка к плавной кривой распределения генеральной совокупности. Можно сформулировать ряд критериев такой близости, используя показатели в виде эксцесса, критерия %2 и т. д. [64]. Различные критерии дают несколько различающиеся значения оптимального числа интервалов группирования. Однако сам факт существования оптимума не зависит от выбора критерия близости, так как при группировании данных в слишком большое число мелких интервалов некоторые из них окажутся пустыми или мало заполненными. Гистограмма будет отличаться от плавной кривой распределения вследствие изрезанности многими всплесками и провалами. [c.37]
Шторм Р. [120] рекомендует для определения оптимального числа интервалов формулу Брукса и Каррузера k = 5 lg п. В работе [95] рекомендуется соотношение k = 4п. В работе [52] приводится таблица, согласно которой числа интервалов назначаются от 7 до 22 в зависимости от объема выборки от 40 до 10000. Сравнение указанных рекомендаций, приведенное на рис. 2.2, указывает на близость рекомендаций при п — 100 с последующим увеличивающимся расхождением их по мере увеличения объема выборки. Отдельную группу составляют рекомендации по использованию критерия согласия %2. Применение критерия %2 к интервалам постоянной длины неэффективно [64]. Исходная посылка всех работ по эффективности критерия х2 — рассмотрение интервалов с равной вероятностью. Однако практически эти рекомендации не используются из-за сложности их применения. Учитывая разнородность перечисленных рекомендаций, возникает необходимость отдельного исследования влияния числа интервалов при использовании информационных методов анализа технологических процессов. [c.38]
Можно выбрать 6 или 7 интервалов. Определяем зону рассеяния размеров R. Устанавливаем максимальное значение размера х = 0,126 и минимальное хт а= — 0,149, размах R = дгтах - xmin = 0,275 мм. Выбираем 7 интервалов и определяем их цену деления С = RI k 0,04 мм. Подсчитаем число отклонений размеров, попавших в соответствующий интервал. Результаты (табл. 2.5) позволяют выдвинуть гипотезу о распределении исследуемых погрешностей по закону Гаусса. Для проверки гипотезы необходимо подготовить данные, входящие в состав информационного критерия согласия J [см. формулу (2.20)]. [c.43]
Смотреть страницы где упоминается термин Критерий согласия
: [c.462] [c.189] [c.171] [c.63] [c.99] [c.471] [c.94] [c.207] [c.472] [c.35]Смотреть главы в:
Моделирование и управление в экономике Часть 1 -> Критерий согласия
