Математическая модель задачи оптимального компаундирования представляет собой частный случай общей задачи линейного программирования о смесях. При построении математической модели процесса необходимо учитывать те же условия и ограничения, которыми руководствуются при объемных расчетах компаундирования, например подчиненность компонентов правилу аддитивности, приемистость их к ГЭС, технические условия на нефтепродукты согласно ГОСТ, ресурс каждого компонента и др. [c.134]
Задачи линейного программирования направлены на нахождение способа эффективного использования или распределения ограниченных ресурсов для достижения поставленных целей. Условия задачи записывают в виде системы линейных уравнений или неравенств (системы ограничений), а результат в виде целевой функции, являющейся суммой произведений найденных значений переменных на присваиваемые им показатели эффективности. Искомыми неизвестными величинами могут быть, например, различные виды оборудования. Коэффициенты при неизвестных в системе ограничений являются заданными постоянными числами и выражают удельные затраты. Коэффициенты при неизвестных в целевой функции — также постоянные величины. Они могут представлять собой себестоимость, цену оборудования, материалов, степень загрузки оборудования и т. п. Свободные члены в ограничениях — это величины тех или иных ресурсов, которые нужно распределить оптимальным образом (запасы материалов, фонды времени работы оборудования). [c.153]
После того, как задача сформулирована в терминах линейного программирования, решение ее состоит в применении того или иного расчетного алгоритма. Наиболее распространенными методами решения задач линейного программирования являются симплексный (или метод последовательного улучшения плана), распределительный и индексный. Существует также ряд приближенных методов решения, разработанных для отдельных видов задач (пример решения задачи методом линейного программирования дан ниже). [c.153]
Транспортную задачу линейного программирования успешно применяют для планирования перевозок. Другая разновидность ее позволяет выбрать наилучшее местоположение для вновь создаваемых предприятий. [c.146]
Характерным и наиболее распространенным примером задачи линейного программирования является известная транспортная 24 [c.24]
Решаемая задача является статической задачей линейного программирования, хотя с принципиальной точки зрения задача оптимального перспективного планирования должна быть динамической. Поэтому окончательные результаты оптимальности производства и распределения продукции получаются итеративно путем последовательного пересчета показателей на каждой итерации в соответствии с полученными объемами переработки. [c.166]
Оптимизация ТЭБ осуществляется по производственно-транспортной экономико-математической модели, которая формулируется как распределительная задача линейного программирования. Модель ТЭБ страны состоит из 27 районных подмоделей. При необходимости и при наличии исходной информации количество подмоделей (районов) может быть увеличено. В результате оптимизации топливно-энергетического баланса на перспективу определяются [c.209]
Основной математической моделью, используемой для составления оптимальных планов поставок и грузовых перевозок, является транспортная задача линейного программирования. [c.284]
Следовательно, задача определения оптимальной производственной программы предприятия сводится к решению задачи линейного программирования, в которой необходимо найти количество изделий каждого наименования ( X/ = 1,2,. .., п ), которое нужно выпускать за год данным предприятием, чтобы целевая функция [c.116]
Использование такого подхода позволяет перейти от рейтингового метода к построению задачи линейного программирования. [c.182]
Сформулированная задача является задачей линейного программирования и может быть решена даже при [c.141]
В общем виде задача линейного программирования, к которой сводится значительная часть производственно-экономических проблем, может быть сформулирована следующим образом необходимо так выбрать вектор х, составленный из п величин х, . .., х%, чтобы на этом векторе х достигался максимум (или минимум) линейной функции [c.150]
Мы не будем заниматься интерпретацией или свойствами задачи линейного программирования, не будем говорить и о методах ее решения, отметим лишь тот факт, что, кроме методов решения общей задачи линейного программирования, разработано значительное число методов и стандартных программ, предназначенных для решения ее различных частных случаев. Мы рассмотрим два наиболее распространенных класса задач линейного программирования транспортную задачу и обобщенную транспортную (распределительную) задачу. [c.151]
Эта задача проще общей задачи линейного программирования, поскольку ее ограничения имеют весьма специальный вид. Интересно, что к транспортной задаче сводятся проблемы планирования экономических объектов разного типа. Поэтому были предприняты значительные усилия по построению эффективных методов решения транспортной задачи, и эти усилия увенчались успехом. В настоящее время умеют решать задачи транспортного типа значительно быстрее и с большим числом неизвестных, чем обычные задачи [c.151]
Легко заметить, что эта задача отличается от транспортной задачи лишь наличием величин Кц в ограничениях одного из типов (отсюда и одно из названий такой задачи — -задача). Для обобщенной транспортной задачи также разработаны алгоритмы решения, более эффективные, чем алгоритмы решения общей задачи линейного программирования. Транспортная задача проще обобщенной транспортной задачи с точки зрения алгоритма ее решения с помощью ЭВМ, а обобщенная транспортная задача проще общей задачи линейного программирования. При построении моделей их стараются сформулировать так, чтобы свести проблему к возможно более простой задаче. Конечно, такое сведение не должно осуществляться за счет искажения существенных черт изучаемой экономической системы. [c.152]
Заметим, что во втором варианте транспортной задачи с открытой моделью потребитель, спрос которого не будет удовлетворен, выбирается в соответствии с затратами на перевозку грузов. Такой подход верен не всегда часто приходится учитывать в критерии задачи потери потребителей от неполучения грузов, поэтому задача может уже не быть транспортной задачей и даже задачей линейного программирования вообще. Однако если эти потери пропорциональны величине недополученного груза, то критерий остается линейным и мы опять приходим к задаче линейного программирования. [c.156]
Зта задача является задачей линейного программирования общего вида и может быть решена при помощи соответствующих алгоритмов. [c.166]
Поставленная здесь задача оптимального перспективного планирования свелась к задаче линейного программирования, причем довольно частного вида, очень близкого к транспортной задаче. Это большое достоинство модели такого типа, поскольку оказывается возможным решать задачу с большим числом пунктов производства и пунктов потребления. Кроме того, число параметров, входящих в модель, невелико, что облегчает сбор необходимой для расчетов информации. [c.171]
Проведенные нами изменения в модели не приводят к ее принципиальному усложнению. Задача оптимизации по-прежнему остается задачей линейного программирования, так что методы решения остаются прежними. Далее мы рассмотрим модификации модели, которые приведут к изменению типа задачи оптимизации. [c.173]
Сформулированная задача является задачей линейного программирования общего типа. Поставленную здесь задачу выбора оптимального рациона питания часто называют также задачей о диете или задачей о смесях. [c.177]
Без этих и других уточнений исходная задача о выборе оптимального рациона не будет давать правильных решений. Все сформулированные дополнения не выводят задачу за рамки задачи линейного программирования. [c.178]
Обратим внимание читателя на тот факт, что это — задача линейного программирования общего типа. [c.179]
Пример 8.9. Задача линейного программирования графическое решение [c.367]
На первой стадии решения данной задачи линейного программирования сформулируем ограничения алгебраически так, обозначив количество единиц краски буквой х, а лака — у, получим [c.367]
| Рис. 8.3. Графическое решение задачи линейного программирования | 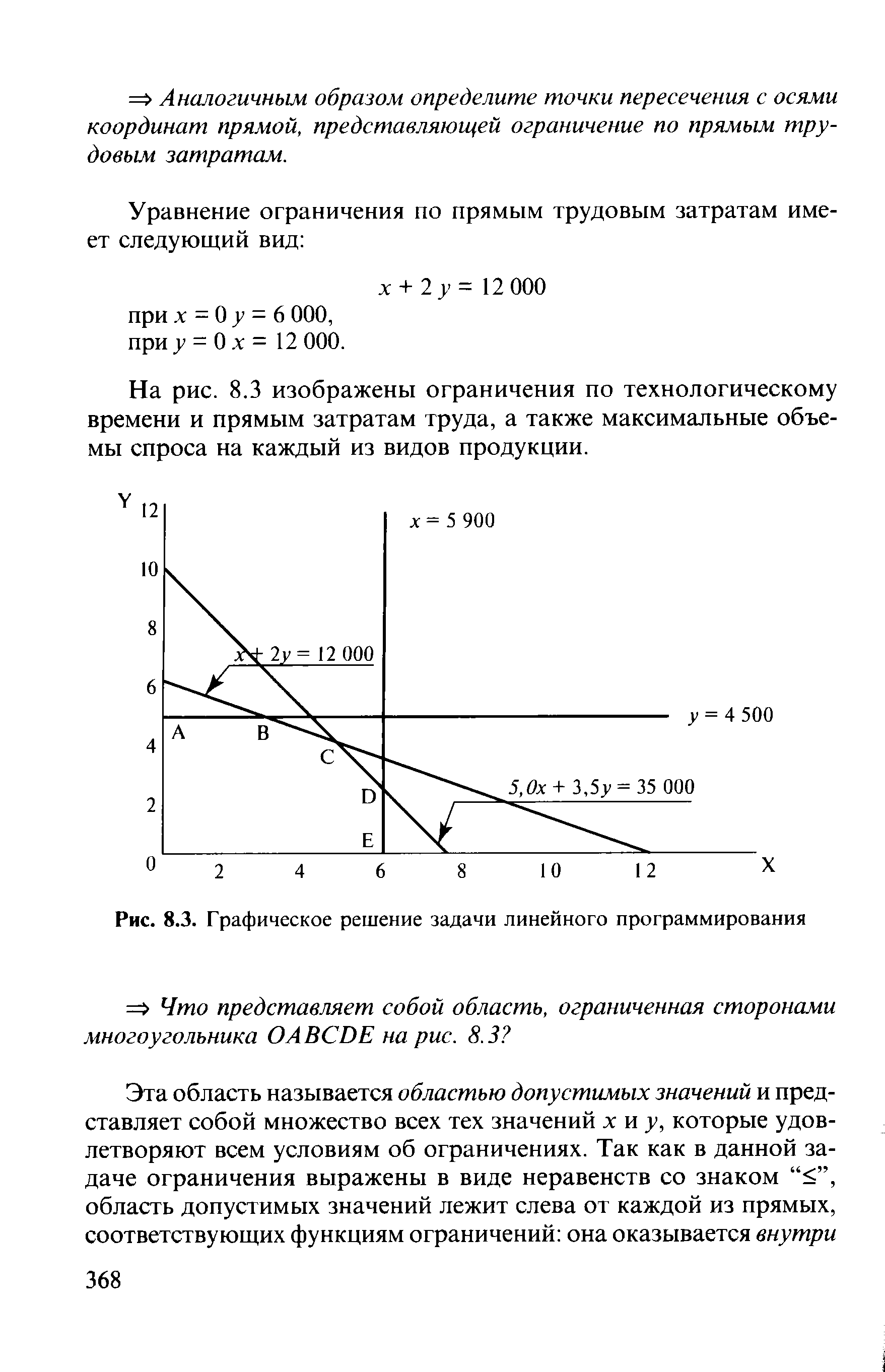 |
В случае, если видов товара всего два, задачу линейного программирования можно решить графически. [c.378]
На рис. 8.4 представлено графическое решение задачи линейного программирования. Известно, что все ограничения, изображенные на рис. 8.3, являются неравенствами со знаком "<". Какова область допустимых значений [c.380]
Новый этап в развитии методов экономико-математического моделирования начался в конце пятидесятых годов, когда появление вычислительной техники сделало многовариантные плановые расчеты на основе экономико-математических моделей реализуемыми по крайней мере принципиально. На развитие экономико-математических методов в это время большое влияние оказали работы Л. В. Канторовича, который в результате анализа некоторых задач планирования производства сформулировал новый важный для экономики класс математических задач, получивших название задач линейного программирования. В линейном программировании рассматривается вопрос о поиске среди всех допустимых решений, удовлетворяющих системе линейных равенств и неравенств, наилучшего (оптимального) решения, доставляющего максимум (или минимум) некоторому линейному критерию. В настоящее время линейное программирование является основным математическим методом анализа задач планирования производства. [c.16]
В общем виде задачу линейного программирования можно представить в следующей форме [c.50]
Как мы уже говорили в предыдущем параграфе, множество, описываемое системой (4.23), (4.24), является выпуклым и многогранным. В связи с линейностью критерия (4.22) можно утверждать, что решение задачи (если, конечно, оно существует) достигается па границе множества допустимых решений (4.23), (4.24), его выпуклость гарантирует, что найденный локальный максимум будет совпадать с глобальным. Поскольку это множество является многогранным, то из линейности критерия следует, что решение достигается в вершине множества. Если решение задачи (4.22) —(4.24) не единственно (например, целая грань множества), то среди решений хотя бы одно является вершиной. На этом. факте основано большинство методов решения задач линейного программирования. [c.50]
Рассмотрим, например, задачу линейного программирования, уже встречавшуюся в предыдущем разделе [c.51]
Как видно, описанный здесь метод решения, основанный на полном переборе вершин, является значительно более простым л эффективным, нежели непосредственное использование метода множителей Лагранжа. В то же время не следует считать, что решение задач линейного программирования является простым делом, состоящим просто в полном переборе вершин множества допустимых значений переменных. Для того чтобы понять это, достаточно заметить, что вершина множества допустимых точек (в том случае, когда это множество имеет внутренние точки) в задаче (4.22) — (4.24) связана с обращением в равенства п ограничений из их совокупности (4.23), (4.24). Таким образом, вообще говоря, число вершин множества (4.23), (4.24) может равняться числу различных сочетаний по п ограничений из общего числа т + п. Число различных сочетания [c.51]
Для того чтобы получить обшее представление об используемых сейчас методах решения задач линейного программирования, вернемся к нашей простой двумерной задаче. Рассмотрим произвольную вершину, например xw. Для нее Шж(1))=0. Затем рассмотрим какую-либо соседнюю вершину, например х(г Имеем U(xm — 1 > U(x(l ). Эта вершина предпочтительнее исходной (1), поэтому переходим в нее. Далее, взяв за исходную вершину ж(2), рассмотрим соседние с ней вершины. Одна из них, ж(3), предпочтительнее ж(2>, так как U(xw) = 10/7 > U(x(Z ). Переходим в эту вершину и сравниваем ее с соседними, хт и xw. Как видно, они являются менее предпочтительными. В силу выпуклости задачи линейного программирования найденный локальный максимум совпадает с глобальным. Поэтому в точке ж<3) находится решение поставленной задачи. [c.52]
Существуют методы, в которых решение задачи линейного программирования находится точно за бесконечное число шагов. [c.53]
Характерный и наиболее распространенным примером задачи линейного программирования является известная транспортная задача. Сущность этой задачи состоит в следующем. В различных пунктах производства имеется однородный груз (например, однотипные яелезобетонние пригруэы), который требуется доставить в несколько пунктов потребления (участков балластировки трубопроводов). Известно, сколько груза производится в каждом пункте и сколько должно поступить в каждый пункт потребления. Требуется определить такой план перевозки грузов, который обеспечивает общие минимальные затраты на транспортировку. [c.5]
Разработанный комплекс средств первой очереди математического обеспечения применялся в основном для решения отдельных задач функциональных подсистем АСПР на ЭВМ разных типов с использбванием общесистемного математического обеспечения АСПР. В этот комплекс входят программы ввода информации ( Документ ) и средства программирования процедурно-ориентированное математическое обеспечение для ЭВМ Минск-32 , система программ Счет-1 , типовые средства обработки данных на ЭВМ, типовые программы статистического анализа, задач линейного программирования, программы решения информационно-поисковых задач, терминальной отладки программ, универсальные программы печати таблиц, комплекс программ обмена данными между ЭВМ Минск-32 и ЕС ЭВМ через магнитные ленты в соответствии со стандартами системы Документ . [c.174]
При решении задач (3) (5) и (4) (5), которые представляют собой две классические однокритериальные задачи линейного программирования, получаем крайне противоречивые результаты. В первом случае цена Ц равна нулю, а доля накладных расходов вуза л стремится к максимуму и превышает 100 %. Во втором случае получаем обратную ситуацию, когда Ц достигает своего максимального уровня, а А. рана нулю. Таким образом, можно сделать вывод, что критерии А, и Ц являются крайне противоречивыми. В связи с этим необходимо найти некое компромиссное решение. Компромисс в этом случае будет заключаться в том, что мы ослабляем требования по каждому критерию и вводим критерий согласия, обозначив его через переменную j.. Максимальное значение критерия согласия равно 1 [2]. [c.26]
Если jt Jo, то в условии (11) будут присутствовать искомые коэффициенты а (i //), для которых далжны применяться условия (4) -(8). Исходя из правила выбора столбца для ввода в базис, значения ati должны минимизировать выражение (11). Для нефтеперерабатывающего производства условия (4) — (8) образуют задачу линейного программирования с. Целевой функцией (11) которую будем называть вспомогательной. Поскольку с имеет фиксированное значение, то вспомогательная задача будет иметь вид . - . [c.99]
В нескольких следующих параграфах мы рассмотрим различные задачи планирования, сводящиеся к задаче линейного программирования одного из трех видов. Приво- [c.152]
Графическим методом можно решать задачи линейного программирования с любым количеством ограничений (в отличие от рассмотренного выше метода оценки вклада в расчете на единицу ограничивающего фактора). Однако он применим только к двухпродуктовым моделям, так как каждому товару/услуге должна соответствовать одна координатная ось. [c.370]
Пример 8.10. Решение задачи линейного программирования средствами пакета LINDO [c.372]
Для построения двойственной задачи обратимся к методу множителей Лагранжа, который хотя и не эффективен при решении задач линейного программирования, но полезен для их качественного анализа. Функция Лаграижа для задачи (4.22) — (4.24) имеет вид [c.53]
