| Рис. 8.3. Графическое решение задачи линейного программирования | 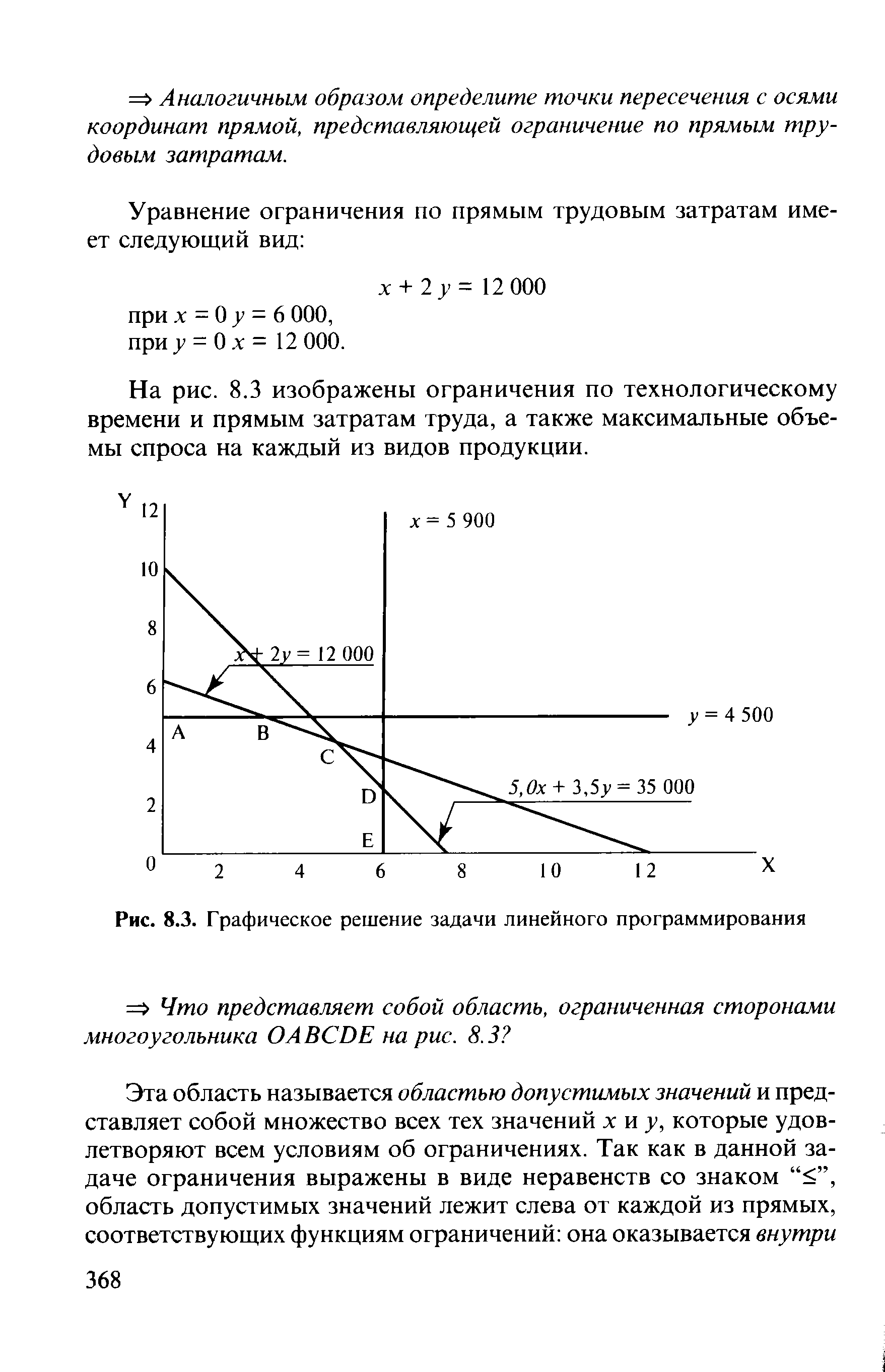 |
Графическое решение задачи показано на рис. 12.4. По горизонтали показывается объем реализации продукции в процентах от производственной мощности предприятия, или в натуральных единицах (если выпускается один вид продукции), или и денежной оценке (если график строится для нескольких видов продукции), по вертикали — себестоимость проданной продукции и прибыль, которые вместе составляют выручку от реализации. [c.239]
| Рис. 6.2. Графическое решение задачи деления | 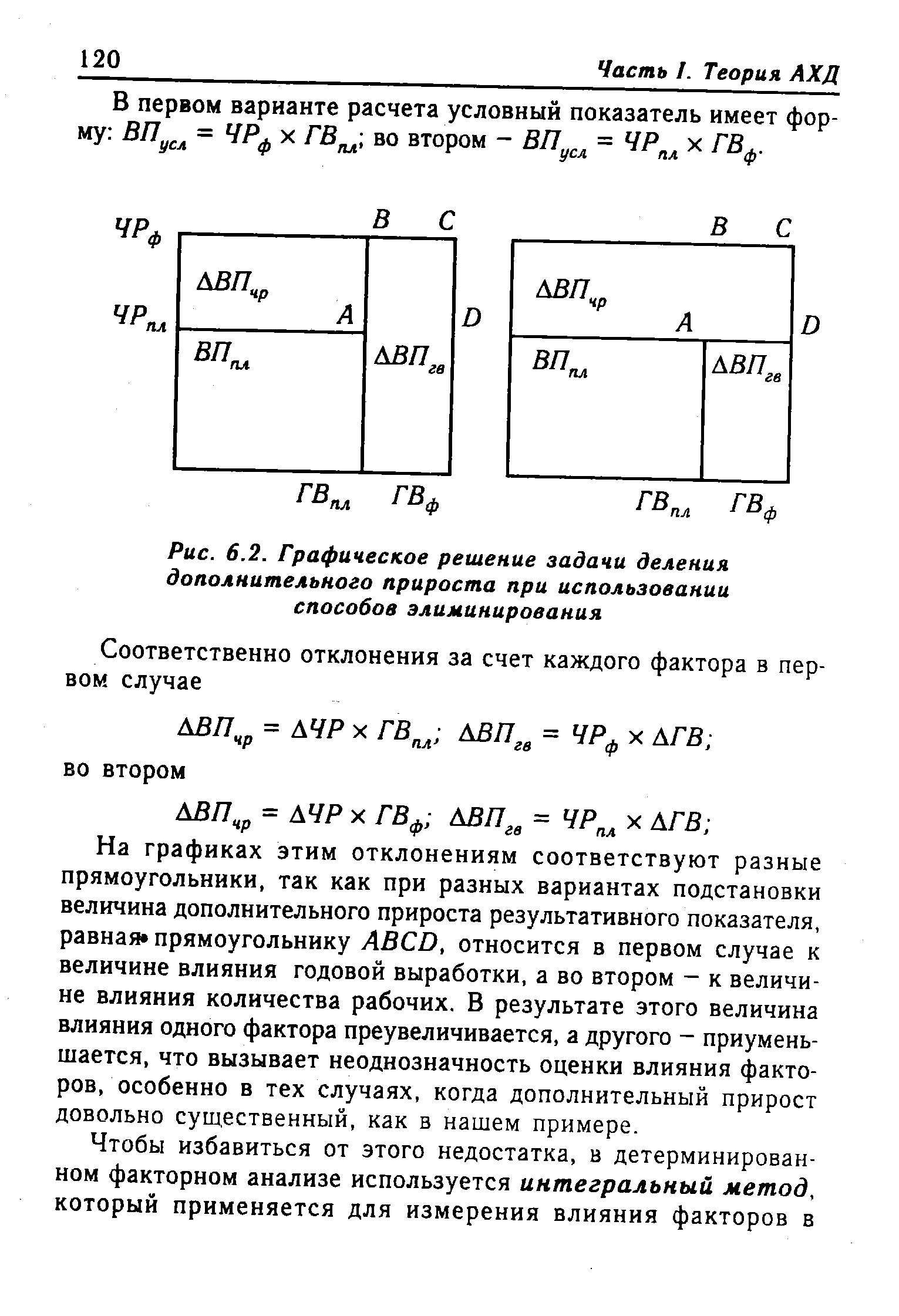 |
Графическое решение задачи (рис. 2.6) показывает, что при равномерном распределении капитальных вложений оптималь- [c.62]
Графическое решение задачи при различных значениях затрат позволяет получить границу АВ, характеризующую зоны рационального использования комплекта машин при вариантах [c.246]
Мы рассмотрим графическое решение задач линейного программирования на данных тех примеров, что приведены в предыдущем разделе. В принципе, метод состоит из двух этапов [c.266]
Давайте рассмотрим решение этой задачи в два этапа (1) Отображение области допустимых решений. Первое, что необходимо сделать при графическом решении задачи, это отобразить ограничения. Рас- [c.266]
Графическое решение задачи определения оптимального уровня запасов приведено на рисунке 3. [c.54]
На рис. 5.3 показано графическое решение задачи разложения прироста объема продукции на составляющие в соответствии с влиянием отдельных факторов для случая, когда один фактор растет (например, производительность труда, т.е. W > W), а другой — уменьшается (например, затраты труда, т.е. 71 < То). Площадь заштрихованного прямоугольника / соответствует приросту объема продукции за счет изменения производительности труда, а площадь прямоугольника 2 — уменьшению объема продукции за счет сокращения затрат труда. Совокупное изменение объема продукции за счет двух факторов соответствует разности площадей указанных прямоугольников. Если площадь прямоугольника / больше площади прямоугольника 2, то общий прирост объема продукции будет положительным, в противном случае — отрицательным. [c.79]
Графически решение задачи на поиск наилучшей комбинации факторов аналогично решению задачи потребительского вы- [c.209]
Графическое решение задачи об оптимальном плане выпуска продукции мебельного цеха [c.56]
Графическое решение задачи об оптимальном плане мебельного цеха [c.57]
| Рис. 1.21. Графическое решение задачи об оптимизации смеси | 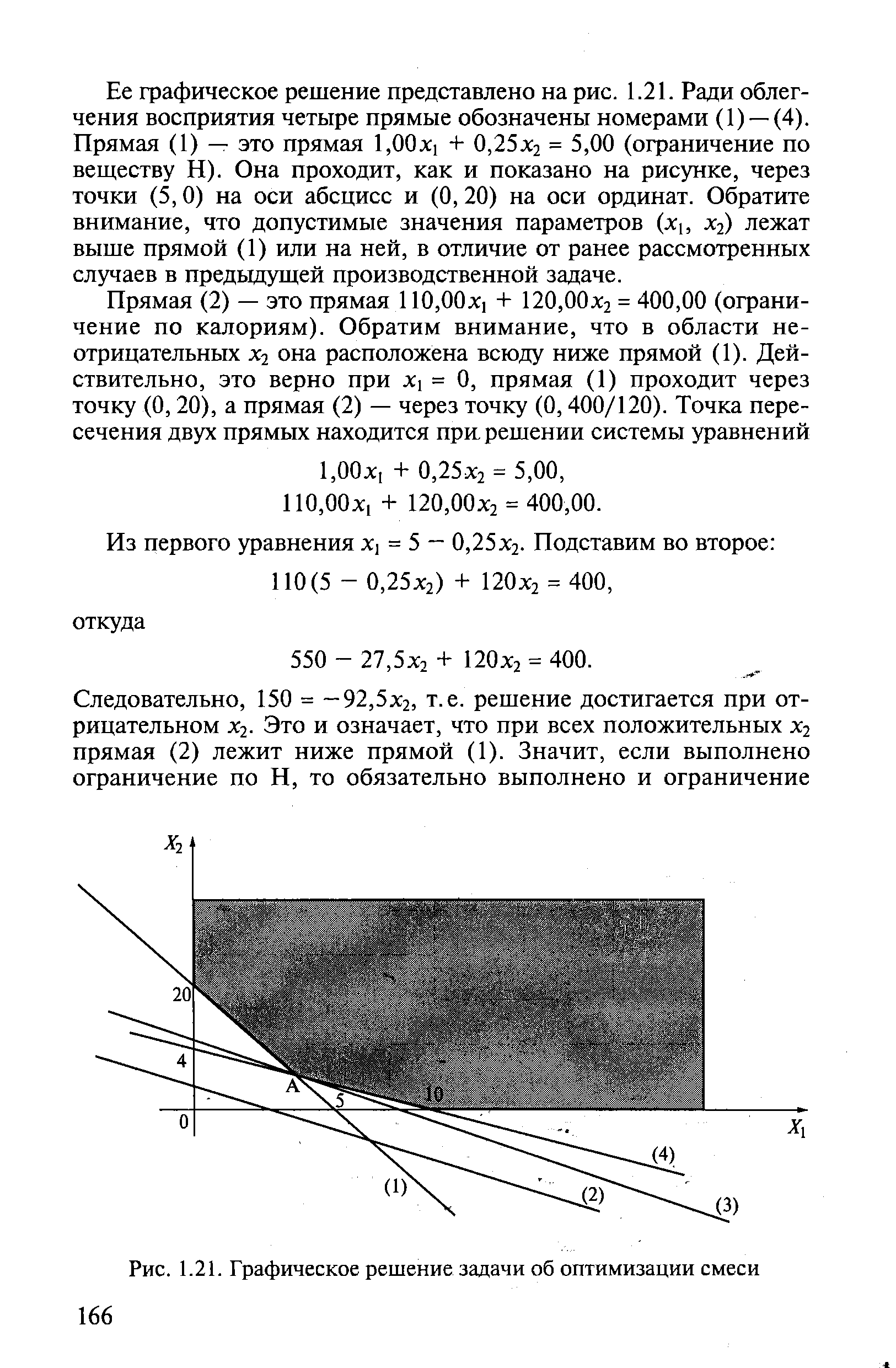 |
На рис. 4.5, а, б, в, приведено графическое решение задачи для различных случаев в зависимости от того, где находится q по отношению к зонам 1,2,3. [c.558]
Рис. 4.5, а,б,в. Графическое решение задачи для трех случаев [c.560]
Графическое решение задачи [c.413]
При графическом решении задачи мы ограничивались двумя компонентами. Но для составления смеси требуемого состава могли быть использованы и другие компоненты. Для решения задачи при п компонентах, если заданы т ограничений, целесообразно применить симплексный метод. Он позволяет находить допускаемое решение и осуществлять последующие систематические переходы к другим допустимым решениям, предусматривающим меньшую стоимость. При этом необходимо установить, является ли данное решение оптимальным и каким образом следует производить переходы от одной точки к другой, чтобы уменьшить стоимость требуемой смеси. Симплекс метод дает ответы на эти вопросы, и решение будет оптимальным, если какой-либо использованный компонент дает чистый выигрыш. [c.191]
Суть графического решения задачи заключается в сложении двух зависимостей и нахождении точки минимума у полученной суммы (рис. 5.2.1). [c.156]
Зи , = /(а), получим сумму (П"п +3"3 ) =/(< ). Это графические решение задачи. [c.161]
Покажем графическое решение задачи в разных вариантах (рис. 6.2). [c.117]
Наилучший способ графического решения задачи — построение графика зависимости прибыли от объема реализации по каждому варианту (рис. 18.7). [c.457]
Графическое решение задачи 2 при двух заготовках. Чтобы графически решить задачу 2, можно действовать в порядке, совершенно аналогичном ходу решения задачи 1, с той только разницей, что, во-первых, придется рассматривать возможные раскрои для каждого из габаритов материала, который можно использовать, и, во-вторых, точки, соответствующие каждому из возможных раскроев, следует наносить на вспомогательный график по несколько иному правилу. Для каждого раскроя изображающая его точка строится таким образом, что ее координата х принимается равной отношению числа получаемых заготовок первого вида к весу расходуемого целого куска материала. Вместо веса можно брать объем, длину, площадь, стоимость — в зависимости от того, по какому из показателей мы должны добиться минимального значения для расходуемого материала. Координата у берется равной отношению числа получаемых при этом раскрое заготовок второго вида к весу (или другому показателю) расходуемого куска. [c.23]
Графическое решение задачи 3 уже при двух заготовках значительно сложнее. Мы не будем здесь его приводить. [c.25]
Подготовьте графическое решение задачи для диапазона от 0 до 2000 ед. [c.42]
Графическое решение задачи представлено на рис. 3.32., Пх = 15х + 60 000 х = 30 000. При потреблении менее 30 000 прутков в год покупать их выгоднее на стороне. [c.265]
ЦХ) Рис. 2.2. Графическое решение задачи № 2.01 [c.33]
| Рис.2.3. Графическое решение задачи №2.02 | 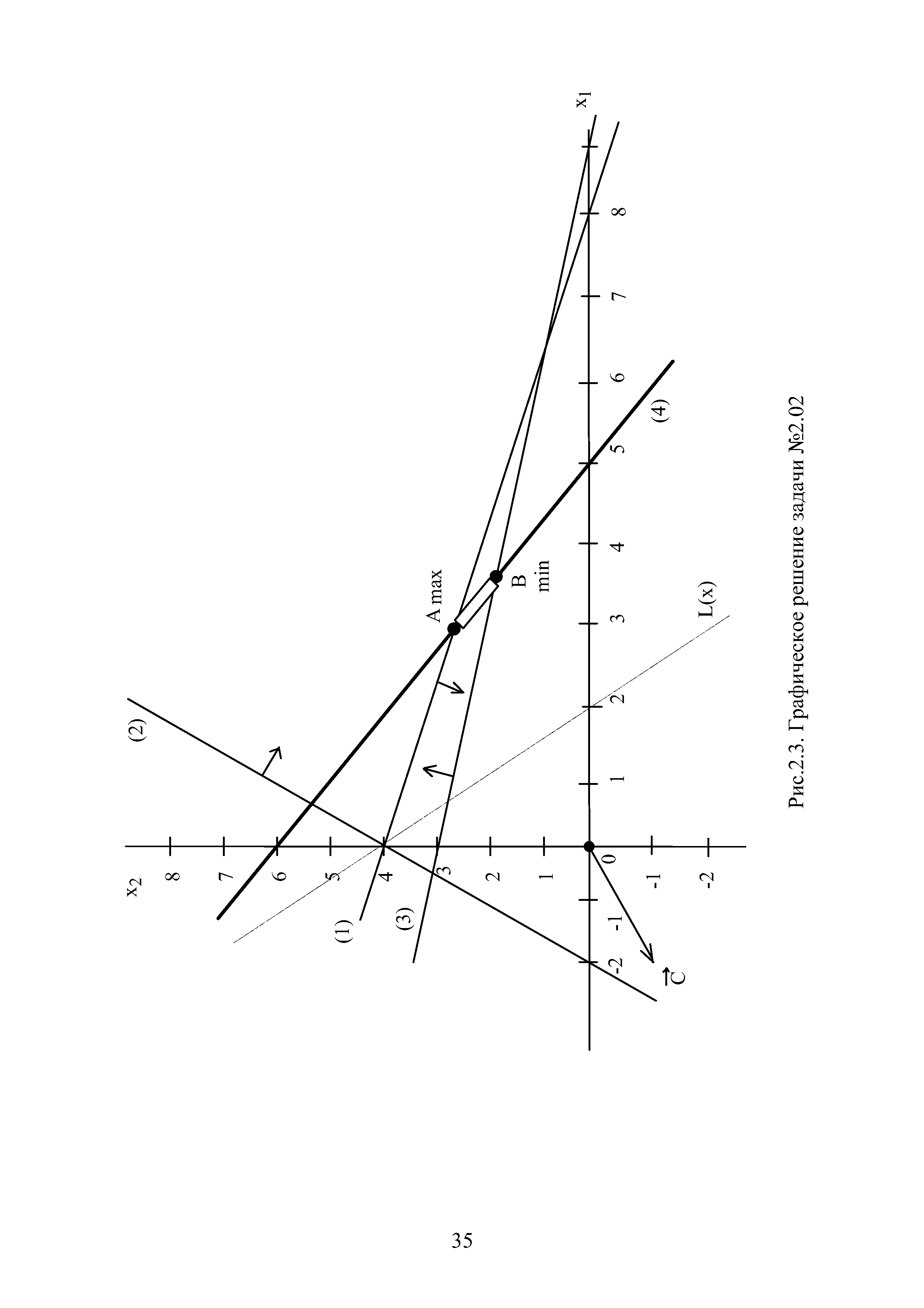 |
| Рис. 2.4. Графическое решение задачи № 2.03 | 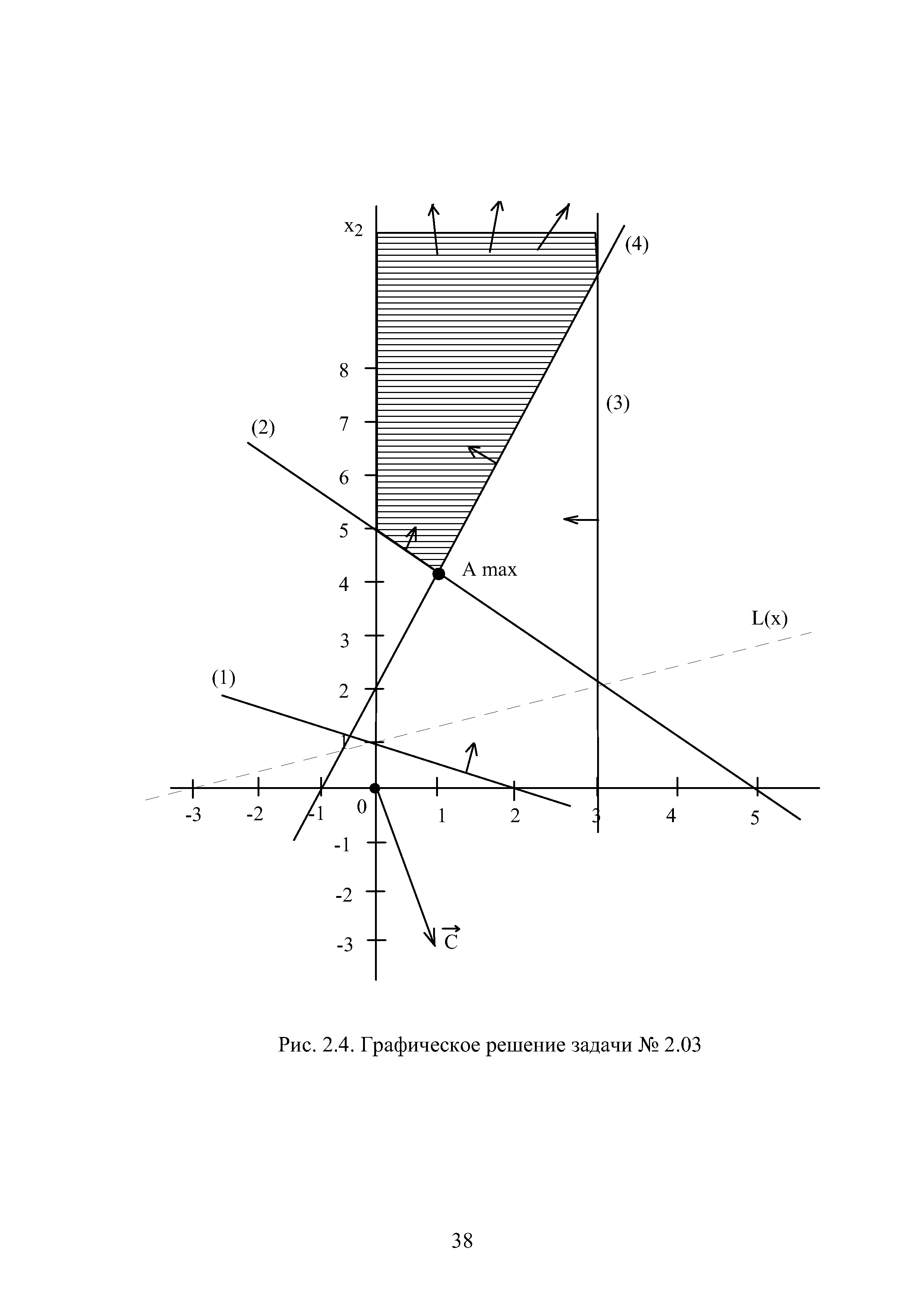 |
| Рис. 3.1. Графическое решение задачи № 1.01 о красках | 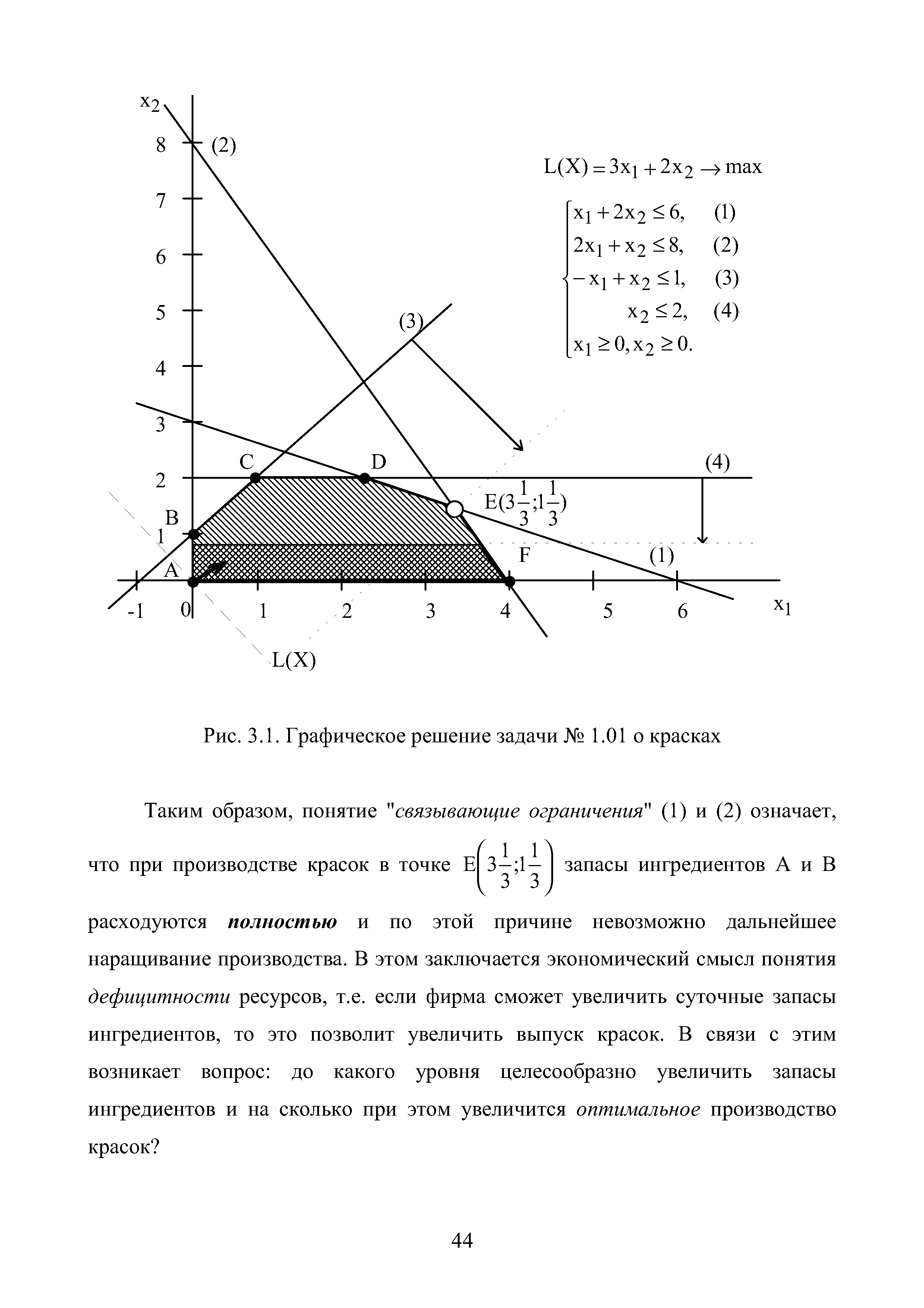 |
Однородность нулевой степени данных функций означает, что если все цены и доход потребителя изменятся в одно и то же число раз, то количество каждого из благ, покупаемых потребителем на рынке, останется неизменным. Покажем это для случая двух благ, используя графическое решение задачи потребительского выбора. [c.30]
Построить график безубыточности для графического решения задачи (диапазон — 0—2000 единиц). [c.426]
Д5Ягв = 200000 - 160000 = +40000 млн руб. Покажем графическое решение задачи в разных вариантах (рис. 6.2). [c.119]
Продемонстрируем однородность нулевой степени относительно цен данных функций для случая двух благ, используя графическое решение задачи минимизации расходов. Рассмотрим рис. 2.2. На графике видно, что при первоначальных ценах (j915j92) и требуемом уровне полезности С/3 наш потребитель выбирает набор [c.37]
Построить график безубыточности для графического решения задачи и определить тенденцию изменений операционной прибыли при различных уровнях активности [c.426]
