| Рис. 8.3. Графическое решение задачи линейного программирования | 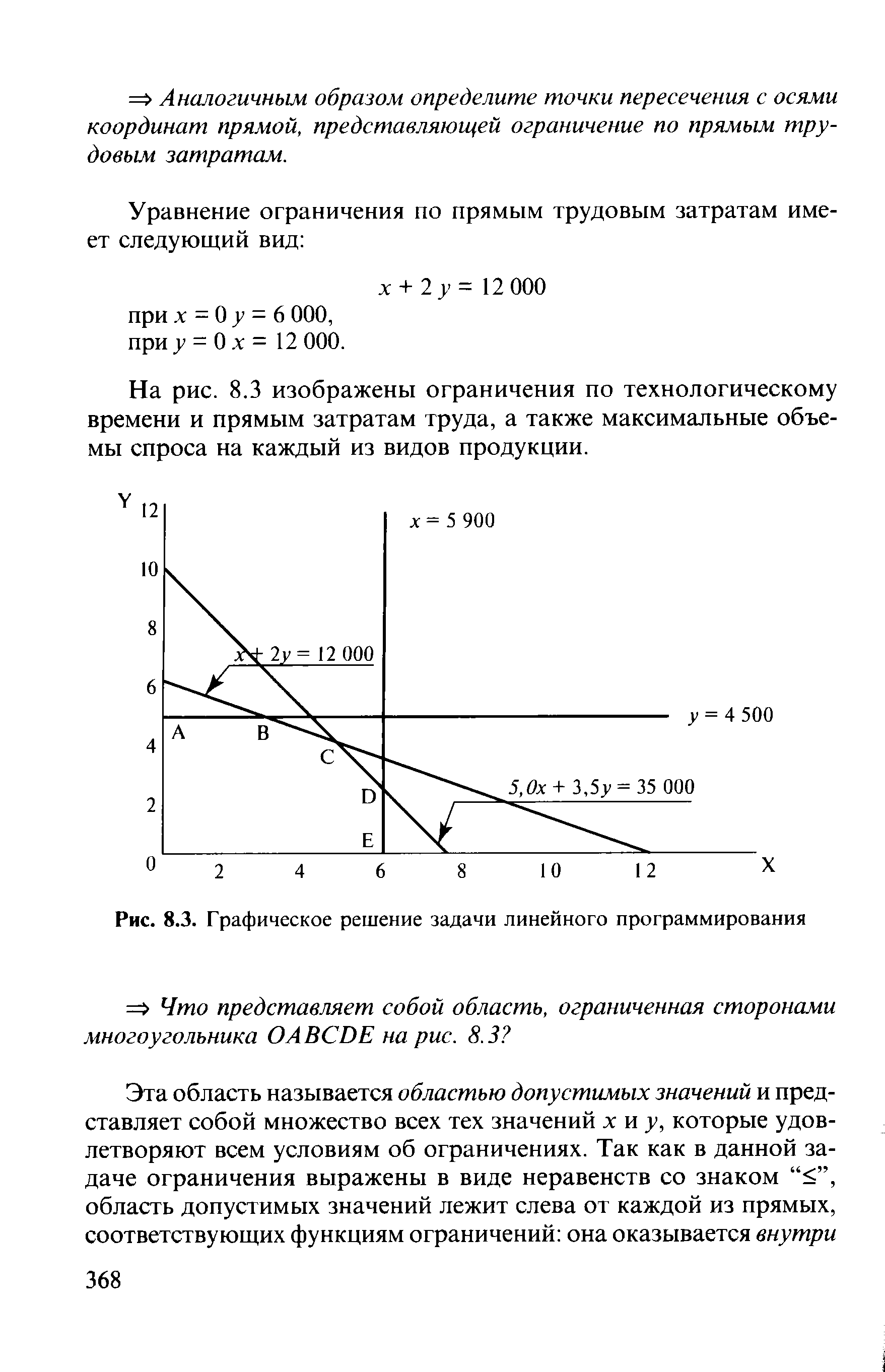 |
Мы рассмотрим графическое решение задач линейного программирования на данных тех примеров, что приведены в предыдущем разделе. В принципе, метод состоит из двух этапов [c.266]
Ситуации такого рода, требующие максимизации или минимизации заданного линейного выражения зависимости от различных линейных ограничений, или сдержек, могут быть разрешены с помощью линейного программирования. В данной главе представлены базовые приемы решения задач линейного программирования с помощью графических и других аналитических средств. [c.261]
На последующих примерах мы рассмотрим графический метод решения задачи линейного программирования. В предыдущем примере мы рассматривали задачу максимизации, где все ограничения были выражены в виде неравенств, т. е. < . В принципе, задачи линейного программирования могут иметь различные по виду ограничения, то есть там может быть сочетание >,< и =. Но и задачи минимизации также важны. Так, компания может поставить задачу минимизировать затраты, рабочее время и убытки. На последующих примерах мы и рассмотрим применение графического метода в таких случаях. [c.272]
Как мы уже отмечали, графические методы, описанные в предыдущих разделах, приемлемы только в отношении задач с не более чем двумя неизвестными (например, х и у). В большинстве практических ситуаций число неизвестных может быть гораздо большим. Симплексный метод — один из наиболее известных подходов к решению задач линейного программирования через алгебраические методы. Симплексный метод применяется в самых разнообразных компьютерных программах, предназначенных для решений таких задач. [c.279]
Линейное программирование — математический метод, предназначенный для выявления оптимального решения из большого числа возможных вариантов решения задачи, у которой условия позволяют запись в виде линейных соотношений. Линейное программирование применяется для решения задач типа распределение ресурсов, формирование комбинации кормов, составление портфеля инвестиций, выбор производственной программы. Для постановки задачи линейного программирования необходимо ввести переменные (определяемые) величины, выразить через эти переменные ограничивающие условия и целевую функцию. Для решения задач линейного программирования используют симплекс-метод или графический метод (при наличии двух переменных в решаемой задаче). [c.122]
Решение задач линейного программирования с двумя элементами решения, подобных задаче в рассматриваемом примере, можно получить даже графически. Но на практике для решения используют компьютеры. [c.113]
Для того чтобы сформировать интуитивное представление о том, как может меняться решение задачи линейного программирования при изменении параметров, полезно получить и проанализировать графическое решение нашего первого "игрушечного" примера об оптимальном плане мебельного цеха, а также познакомиться с понятием двойственности задач линейного программирования. [c.55]
Таким образом, графическое решение никоим образом нельзя рассматривать как практический метод решения задач линейного программирования. Однако проведенный графический анализ дает [c.59]
Графический способ решения задач линейного программирования целесообразно использовать для [c.202]
Пример 8.9. Задача линейного программирования графическое решение [c.367]
В этой главе мы рассмотрели приемы линейного программирования при решении задач оптимизации. Типичный пример — максимизация прибыли предприятия за счет определения соответствующей номенклатуры производства. Кроме того, задачи линейного программирования могут быть направлены на минимизацию переменных, в частности затрат. Выражение, которое необходимо оптимизировать, называется объективной функцией. Эта функция высчитывается при наличии ряда ограничений. Одна из самых больших трудностей при решении такого рода задач состоит в исходной постановке задачи, когда необходимо определить ограничения, представить их в виде неравенств и выдать выражение объективной функции. При решении простых задач только с двумя переменными можно применить графический метод. Для более сложных задач применяется симплексный метод. [c.304]
Представьте графическое решение для следующей задачи линейного программирования. [c.457]
Таким образом, с геометрической точки зрения задача максимизации сводится к определению такой точки области Д через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Последнее означает, что для нахождения точки экстремума в задаче линейного программирования мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем необходимо осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору с) до тех пор, пока не достигнем такой точки области допустимых планов Д из которой смещение в направлении вектора с было бы невозможно. Такой метод решения получил название графического. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с). [c.25]
Графические методы решения игр. Следует отметить, что применение для решения задач (6.16)-(6.17), (6.18)-(6.19) стандартных алгоритмов линейного программирования далеко не всегда является рациональным. Помимо этого существуют иные методы, которые основываются на использовании специфики данных задач. В настоящем пункте мы остановимся на очень простом классическом способе поиска оптимальных смешанных стратегий в матричных играх, где один из участников имеет только две стратегии (это так называемые 2 х п и т х 2 игры). [c.194]
Задача об использовании оборудования. Ход решения задач симплексным методом рассмотрим на примере загрузки оборудования, который был использован в одной из предыдущих глав, при изложении графического метода линейного программирования. [c.298]
Наибольшее распространение в экономике в настоящее время получили математическое программирование и статистические методы. Правда, для представления статистических данных, для экстраполяции тенденций тех или иных экономических процессов всегда использовались графические представления (графики, диаграммы и т.п.) и элементы теории функций (например, теория производственных функций). Однако целенаправленное применение математики для постановки и анализа задач управления, принятия экономических решений разного рода (распределения работ и ресурсов, загрузки оборудования, организации перевозок и т.п.) началось с внедрения в экономику методов линейного и других видов ма- [c.60]
Если задача теории игр не имеет решения в чистых стратегиях и не может быть решена графически, то для получения точного решения игры используют методы линейно-го программирования. > Целесообразно задачу х ВТОрОГО игрока решать сим-Рис. Ю.1 плекс-методом. В послед- [c.252]
В этом разделе мы рассмотрим решение задачи линейного программирования с помощью графических методов. Необходимо отметить, что такой метод имеет практический смысл только при рассмотрении двух неизвестных переменных (например, х и у), и он непригоден при решении задач с более, чем двумя неизвестными. Так, если руководитель производства Стенлюкс захочет определиться по количеству трех и более различных моделей холодильников, то в этом случае графический метод применять нельзя. Аналогично, аналитик по инвестициям Вили-Макен не сможет пользоваться графическим методом при оптимизации портфеля из более чем двух акций. То есть вы видите, что графический метод крайне ограничен. Однако он дает полезное представление о том, как вести поиск оптимальных решений, что может оказать помощь при анализе более сложных задач с большим количеством переменных. [c.266]
