Графические методы решения задач [c.472]
| Рис. 1.2. Графический метод решения задачи | 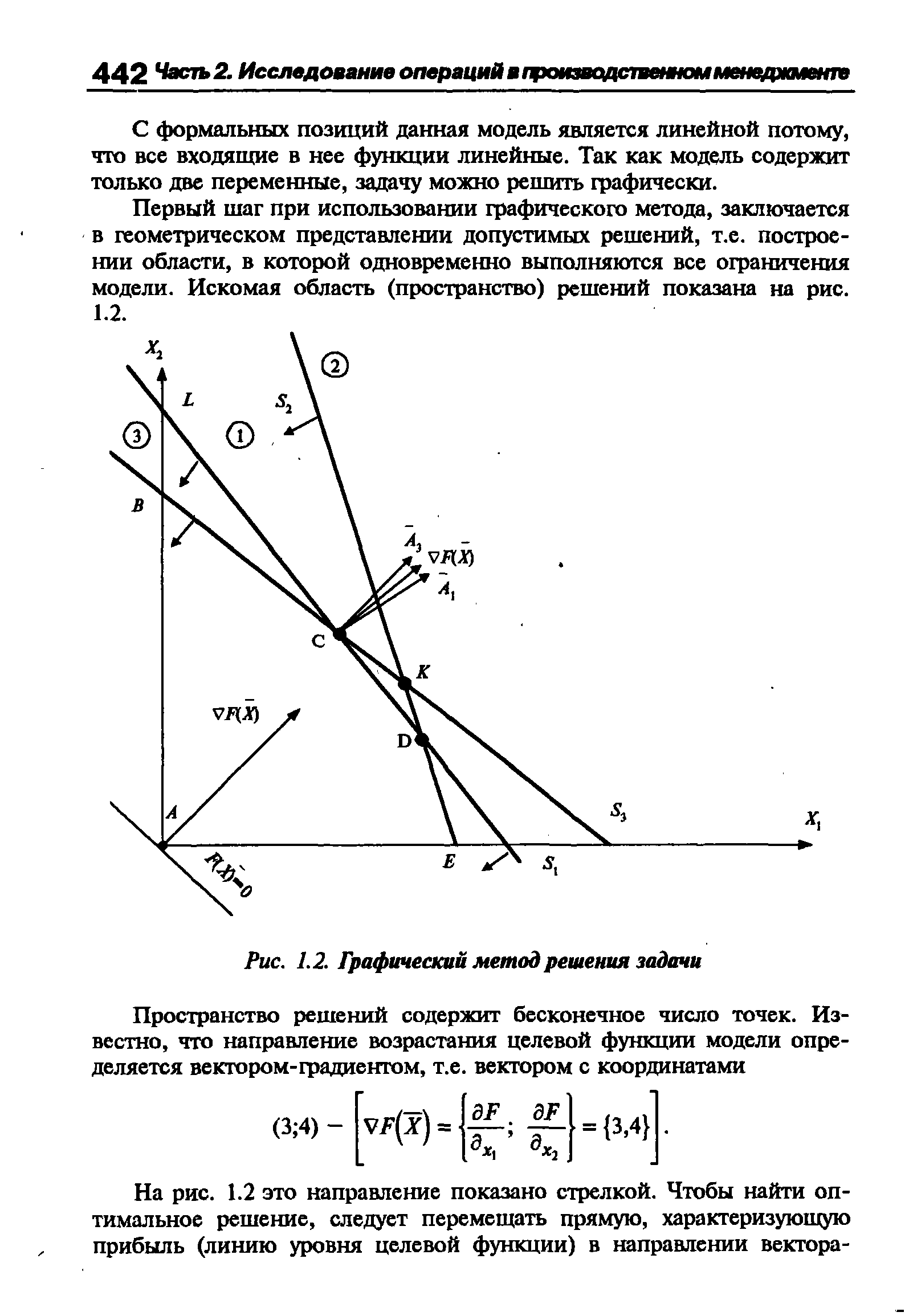 |
ЭВМ семейства СМ, профессиональных персональных ЭВМ. При всех вариантах проектирования АРМ пользователь должен иметь возможность использовать лично устройства, позволяющие ему выполнять должностные функции. К таким устройствам относятся алфавитно-цифровые или графические дисплеи, устройства ввода-вывода, накопители на магнитных носителях. Опосредованное использование могут находить устройства связи ЭВМ между собой и с ЭВМ верхнего уровня, средства передачи и приема информации на расстоянии. Экон. эффект от внедрения АРМ складывается из двух составляющих. Во-первых, это повышение качества управленческих решений, принимаемых с помощью информации, предоставляемой АРМ. Во-вторых, эффект, получаемый за счет снижения трудоемкости выполнения личной работы сотрудников. С помощью АРМ р. целесообразно решать задачи, ограниченные по своим информационным связям на входе и выходе с др. задачами, т.е. локальные в информационном отношении задачи. АРМ р. присущ диалоговый метод решения задач, позволяющий использовать производственный опыт руководителей и специалистов при решении задач с недостаточно четко формализованным алгоритмом. Проектирование и внедрение АРМ р. основывается на принципах проектирования систем обработки данных, основными из которых являются принцип максимальной ориентации на конечного пользователя (реализация данного принципа достигается созданием средств адаптации АРМ к уровню подготовки пользователя и возможностью его обучения (самообучения) непосредственно на данном АРМ) принцип проблемной ориентации — обеспечивает ориентацию АРМ на решение определенного класса задач, объединенных общей технологией обработки данных, единством режимов работы и эксплуатации принцип соответствия информационным потребностям пользователя. К определению состава и функций АРМ р. следует приступать только после установления информационных потребностей пользователя, которые обеспечивают выполнение им возложенных на него функций. Обязательным условием разработки эффективного АРМ р. является совместное участие будущего пользователя и разработчика в этом процессе. Это обеспечивает лучшее осознание всех проблемных ситуаций, стимулирует творческую дея- [c.3]
Q графические методы решения экономических задач и представления результатов анализа [c.436]
Таким образом, графическое решение никоим образом нельзя рассматривать как практический метод решения задач линейного программирования. Однако проведенный графический анализ дает [c.59]
Первая геометрическая интерпретация ЗЛП и графический метод решения. Рассмотрим следующий пример. Пусть дана задача максимизации линейной целевой функции [c.23]
Несмотря на свою очевидную ограниченность, графический метод решения ЗЛП часто оказывается полезным. В частности, он может быть применен не только к задачам с двумя переменными и ограничениями в виде неравенств, но и к каноническим задачам вида (1.7), у которых п - т = 2, где п — количество переменных, am — ранг матрицы А. [c.26]
Графические методы решения игр. Следует отметить, что применение для решения задач (6.16)-(6.17), (6.18)-(6.19) стандартных алгоритмов линейного программирования далеко не всегда является рациональным. Помимо этого существуют иные методы, которые основываются на использовании специфики данных задач. В настоящем пункте мы остановимся на очень простом классическом способе поиска оптимальных смешанных стратегий в матричных играх, где один из участников имеет только две стратегии (это так называемые 2 х п и т х 2 игры). [c.194]
Б. Какая комбинация принтеров и компьютеров будет максимизировать операционную прибыль корпорации IT . Используйте для решения задачи графический метод и метод проб и ошибок. [c.389]
Три первые задачи уже рассмотрены в главе о производственной деятельности. Решение проблемы расчета прибыли предприятия может быть представлено несколькими вариантами применение формул для расчета, графический метод отражения взаимосвязи прибыли и объема производства. [c.258]
При использовании многих аналитических методов на первом этапе часто полезно попытаться графически отобразить полученные данные. Такой подход может привести к решению задачи, и отпадет необходимость прибегать к сложным аналитическим приемам. Но, к сожалению, графическое отображение данных часто недооценивают в качестве инструмента делового общения. График разброса полезен с точки зрения иллюстрации возможного соотношения наборов данных. На последующих примерах мы рассмотрим, как пользоваться этим графиком. [c.100]
Мы рассмотрим графическое решение задач линейного программирования на данных тех примеров, что приведены в предыдущем разделе. В принципе, метод состоит из двух этапов [c.266]
Как мы уже отмечали, графические методы, описанные в предыдущих разделах, приемлемы только в отношении задач с не более чем двумя неизвестными (например, х и у). В большинстве практических ситуаций число неизвестных может быть гораздо большим. Симплексный метод — один из наиболее известных подходов к решению задач линейного программирования через алгебраические методы. Симплексный метод применяется в самых разнообразных компьютерных программах, предназначенных для решений таких задач. [c.279]
В этой главе мы рассмотрели приемы линейного программирования при решении задач оптимизации. Типичный пример — максимизация прибыли предприятия за счет определения соответствующей номенклатуры производства. Кроме того, задачи линейного программирования могут быть направлены на минимизацию переменных, в частности затрат. Выражение, которое необходимо оптимизировать, называется объективной функцией. Эта функция высчитывается при наличии ряда ограничений. Одна из самых больших трудностей при решении такого рода задач состоит в исходной постановке задачи, когда необходимо определить ограничения, представить их в виде неравенств и выдать выражение объективной функции. При решении простых задач только с двумя переменными можно применить графический метод. Для более сложных задач применяется симплексный метод. [c.304]
Известно, что в случае двух переменных решение задачи математического программирования можно провести не только аналитически (например, используя симплекс-метод), но и графически. В нашем примере интерес представляет только целочисленное решение. [c.221]
Линейное программирование — математический метод, предназначенный для выявления оптимального решения из большого числа возможных вариантов решения задачи, у которой условия позволяют запись в виде линейных соотношений. Линейное программирование применяется для решения задач типа распределение ресурсов, формирование комбинации кормов, составление портфеля инвестиций, выбор производственной программы. Для постановки задачи линейного программирования необходимо ввести переменные (определяемые) величины, выразить через эти переменные ограничивающие условия и целевую функцию. Для решения задач линейного программирования используют симплекс-метод или графический метод (при наличии двух переменных в решаемой задаче). [c.122]
В результате проведенных исследований разработаны аналитический и графический методы, позволяющие обосновывать и принимать решения по масштабу, фондоемкости производства, затратам, цене, обеспечивающим заданную прибыльность выпуска продукции. Эти методы позволяют решать и обратную задачу определять уровень относительной прибыли (по отношению к себестоимости) по двум отношениям отношению по- [c.59]
Широкое распространение в мире получила система методов управления проектами, известная в России под названием сетевое планирование и управление (СПУ). Аппарат СПУ предназначен для решения двух основных проблем формирования календарного графика выполнения работ проекта и принятия эффективных решений в процессе его реализации. Эффект, достигаемый при использовании системы СПУ, обусловлен формализацией структуры проекта и количественным выражением его параметров, в первую очередь — временных. Это позволяет использовать строгий математический аппарат и средства вычислительной техники для анализа и синтеза сетевых графиков проектов. Система СПУ — один из наиболее известных примеров использования математического аппарата к решению задач экономико-управленческого характера. Она основана на графическом представлении комплекса работ в виде сетевой модели проекта, которая отражает логические последовательности и взаимосвязи между отдельными работами. Для формального отображения сетевых моделей применяется математический аппарат теории графов. [c.120]
Такая же задача ставится и при составлении бизнес-плана по вновь начинаемому деловому проекту на существующем предприятии. Решение ее позволяет сбалансировать доходы и расходы в рамках утверждаемого и контролируемого бюджета данного проекта. Поставленная задача может быть решена как аналитическим ( формульным ), так и графическим методами. [c.82]
Вероятностные сетки удобны для решения многих задач прикладной статистики графическими методами, не требующими вычислений. В частности с их помощью можно осуществлять оценку согласия опытного распределения с теоретическим, выполнять операции статистического приемочного контроля по количественному признаку и т. п. Они обладают большой наглядностью. [c.26]
При графическом решении задачи мы ограничивались двумя компонентами. Но для составления смеси требуемого состава могли быть использованы и другие компоненты. Для решения задачи при п компонентах, если заданы т ограничений, целесообразно применить симплексный метод. Он позволяет находить допускаемое решение и осуществлять последующие систематические переходы к другим допустимым решениям, предусматривающим меньшую стоимость. При этом необходимо установить, является ли данное решение оптимальным и каким образом следует производить переходы от одной точки к другой, чтобы уменьшить стоимость требуемой смеси. Симплекс метод дает ответы на эти вопросы, и решение будет оптимальным, если какой-либо использованный компонент дает чистый выигрыш. [c.191]
Второй этап — постановка экстремальных задач раскроя, их приближенное и точное решение. Здесь в центре внимания научный анализ возможностей экономии материала при раскрое. Одновременно анализируется роль налагаемых ограничений, а также свобода в технологической реализации оптимальных раскроев. Выделяются подлежащие внедрению решающие моменты в изменении технологии. На первом шаге расчеты ведутся вручную с привлечением подбора и графических методов. Второй шаг — перенос части расчетов на ЭВМ. К этому уровню анализа задач раскроя относится наша книга и большая часть упоминаемой во всем этом обзоре литературы. [c.229]
Выбор методов анализа собранной информации о рынке во многом обусловлен целью работы, квалификацией исследователей, качеством первичной информации, содержанием конкретной задачи. Традиционно для решения задач исследования рынка используются в различных сочетаниях следующие методы группировка, индексный и графический методы, выравнивание и прогнозирование временных рядов, корреляционный и регрессионный анализ, экспертные оценки. Несколько реже применяется метод моделирования [21]. [c.51]
Рассмотрим несколько примеров решения задач графическим методом. [c.347]
Если бы количество заготовок было больше двух, то такой графический способ решения оказался бы слишком сложным, практически трудно реализуемым, так как для изображения множества осуществимых планов потребовалось бы построить многогранник в многомерном пространстве. Для решения задачи в этих случаях на помощь приходят аналитические методы и, в частности, эффективный метод разрешающих множителей— оценок, особых показателей, характеризующих оптимальный план. [c.13]
Если бы количество заготовок было больше двух, то графический способ решения (рис. 3) оказался бы практически трудно реализуемым. Дело в том, что для изображения множества осуществимых планов нужно построить очень сложную геометрическую фигуру — многогранник в многомерном пространстве. Поэтому для решения задачи более рационально использовать аналитические методы и, в частности, эффективный метод разрешающих множителей — оценок, особых показателей, характеризующих оптимальный план. [c.15]
Таким образом, с геометрической точки зрения задача максимизации сводится к определению такой точки области Д через которую проходит линия уровня, соответствующая наибольшему из возможных значений. Последнее означает, что для нахождения точки экстремума в задаче линейного программирования мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции. Затем необходимо осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору с) до тех пор, пока не достигнем такой точки области допустимых планов Д из которой смещение в направлении вектора с было бы невозможно. Такой метод решения получил название графического. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевой функции, т. е. по вектору (-с). [c.25]
Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения основной задачи на решение двойственной, которое в определенных случаях может оказаться более простым. Например, задача, область допустимых значений которой описывается двумя уравнениями, связывающими шесть переменных (т = 2, п = 6), не может быть решена графическим методом. Однако данный метод может быть применен для решения двойственной к ней задачи, которая имеет только две переменные. [c.62]
Решение задач с помощью графического метода содержит элементы не только аналитического, но и графического порядка. Большая наглядность является основным достоинством рассматриваемого метода. Однако область его применения ограничена решением задач с двумя и тремя переменными. [c.188]
Задача об использовании оборудования. Ход решения задач симплексным методом рассмотрим на примере загрузки оборудования, который был использован в одной из предыдущих глав, при изложении графического метода линейного программирования. [c.298]
Среди них можно выделить традиционные логические способы, которые широко применяются и в других дисциплинах для обработки и изучения информации (сравнение, графический, балансовый, средних и относительных величин, аналитических группировок, эвристические методы решения экономических задач на основании интуиции, прошлого опыта, экспертных оценок специалистов и т.д.). [c.15]
Решение задачи произвести аналитическим и графическим методами. [c.364]
В этом разделе мы рассмотрим решение задачи линейного программирования с помощью графических методов. Необходимо отметить, что такой метод имеет практический смысл только при рассмотрении двух неизвестных переменных (например, х и у), и он непригоден при решении задач с более, чем двумя неизвестными. Так, если руководитель производства Стенлюкс захочет определиться по количеству трех и более различных моделей холодильников, то в этом случае графический метод применять нельзя. Аналогично, аналитик по инвестициям Вили-Макен не сможет пользоваться графическим методом при оптимизации портфеля из более чем двух акций. То есть вы видите, что графический метод крайне ограничен. Однако он дает полезное представление о том, как вести поиск оптимальных решений, что может оказать помощь при анализе более сложных задач с большим количеством переменных. [c.266]
Теоретической основой применения графических методов и моделей, по мнению В.М.Цимбалова1, является прежде всего теория графов, которая зародилась в XVIII в. как математическая задача Эйлера о прогулке по замкнутому маршруту в прусском городе Кенигсберге и была развита в XIX в. в связи с возникшей в Англии математической задачей о четырех красках, решенной лишь совсем недавно. В XX в. теория графов прошла определенные стадии формирования и была признана самостоятельной дисциплиной. [c.59]
Смотреть страницы где упоминается термин Графические методы решения задач
: [c.334] [c.33] [c.53] [c.328] [c.28] [c.260] [c.191] [c.213] [c.221] [c.214]Смотреть главы в:
Информационные технологии бухгалтерского учета -> Графические методы решения задач
