| Рис. 8.3. Графическое решение задачи линейного программирования | 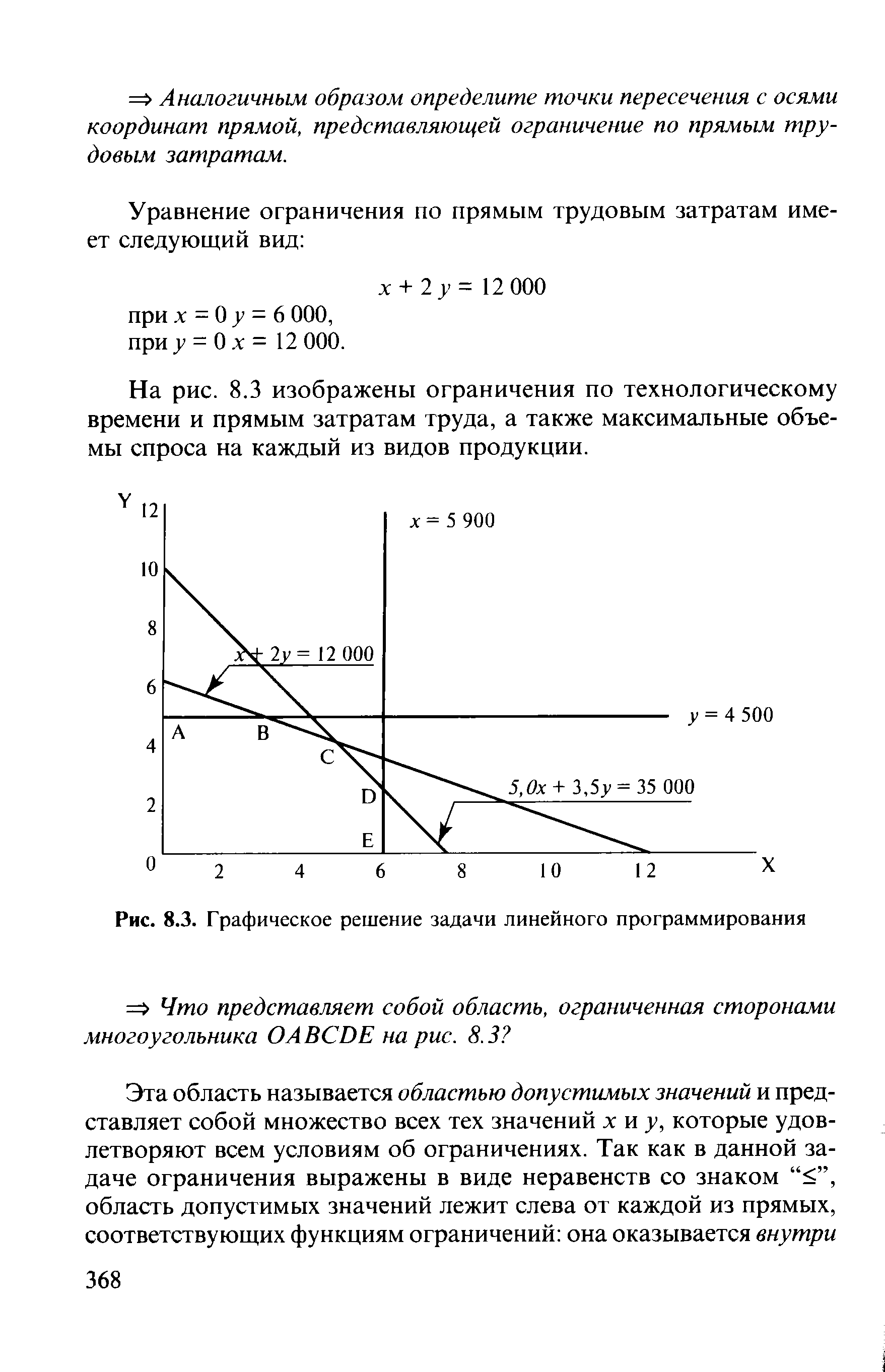 |
Здесь целевая функция — это совокупный вклад, который обеспечивает оптимальный план (60846,160 ф.ст.)- В колонках "Переменная" и "Значение" показано, что для этого необходимо изготовить и реализовать 4307,692 ед. краски и 3846,154 ед. лака. С учетом округления, это совпадает с результатом, который был получен графическим методом. Компьютерная программа предоставляет и дополнительную информацию (ее можно вывести также из графического решения, но лишь косвенным образом), которая может оказаться весьма полезной при принятии решения. [c.373]
На рис. 8.4 представлено графическое решение задачи линейного программирования. Известно, что все ограничения, изображенные на рис. 8.3, являются неравенствами со знаком "<". Какова область допустимых значений [c.380]
| Рисунок 8—1. Линейное программирование — графическое решение | 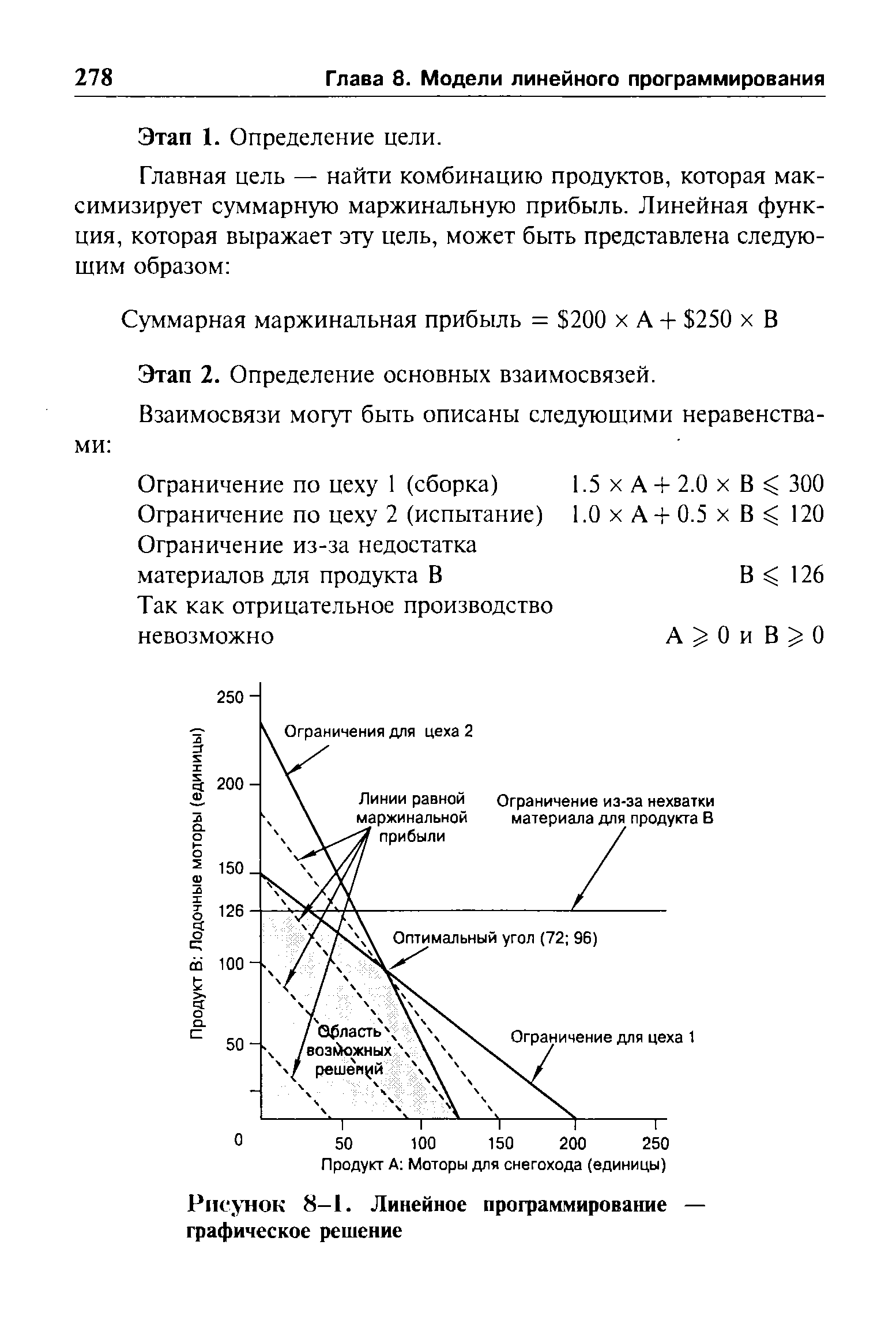 |
ЗАКАЗАННОЕ КОЛИЧЕСТВО (в единицах продукции) Рис. 13.1. Графическое решение проблемы наиболее экономичного размера заказа [c.370]
Графическое решение задачи показано на рис. 12.4. По горизонтали показывается объем реализации продукции в процентах от производственной мощности предприятия, или в натуральных единицах (если выпускается один вид продукции), или и денежной оценке (если график строится для нескольких видов продукции), по вертикали — себестоимость проданной продукции и прибыль, которые вместе составляют выручку от реализации. [c.239]
Линейное программирование — графическое решение [c.383]
| Рис. 6.2. Графическое решение задачи деления | 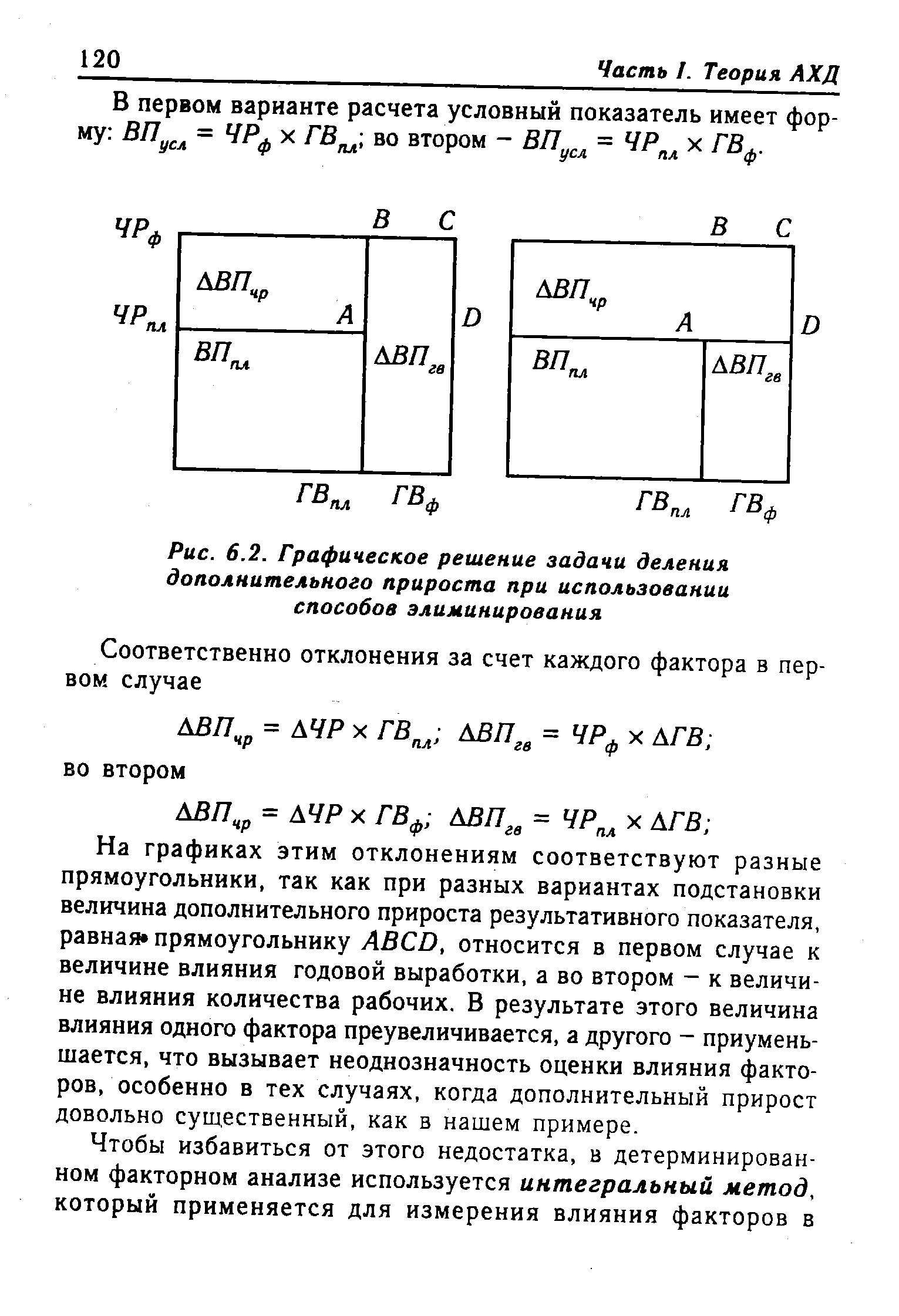 |
Графическое решение задачи (рис. 2.6) показывает, что при равномерном распределении капитальных вложений оптималь- [c.62]
Графическое решение задачи при различных значениях затрат позволяет получить границу АВ, характеризующую зоны рационального использования комплекта машин при вариантах [c.246]
Мы рассмотрим графическое решение задач линейного программирования на данных тех примеров, что приведены в предыдущем разделе. В принципе, метод состоит из двух этапов [c.266]
Давайте рассмотрим решение этой задачи в два этапа (1) Отображение области допустимых решений. Первое, что необходимо сделать при графическом решении задачи, это отобразить ограничения. Рас- [c.266]
Возможно также графическое решение данной задачи. На рис. 2.5 римской цифрой I обозначена линия зависимости прибыли от объема продаж для первого варианта производства, цифрой II — для второго варианта, цифрой III — для третьего варианта. [c.71]
Графическое решение задачи определения оптимального уровня запасов приведено на рисунке 3. [c.54]
Привлекательное графическое решение этикетки способствует продвижению товара. [c.536]
Одно возможное графическое решение [c.919]
Графическое решение данной задачи показано на рис. Р.6. [c.265]
На рис. 5.3 показано графическое решение задачи разложения прироста объема продукции на составляющие в соответствии с влиянием отдельных факторов для случая, когда один фактор растет (например, производительность труда, т.е. W > W), а другой — уменьшается (например, затраты труда, т.е. 71 < То). Площадь заштрихованного прямоугольника / соответствует приросту объема продукции за счет изменения производительности труда, а площадь прямоугольника 2 — уменьшению объема продукции за счет сокращения затрат труда. Совокупное изменение объема продукции за счет двух факторов соответствует разности площадей указанных прямоугольников. Если площадь прямоугольника / больше площади прямоугольника 2, то общий прирост объема продукции будет положительным, в противном случае — отрицательным. [c.79]
| Рис. 1 Графическое решение модели принятия решений (8) | 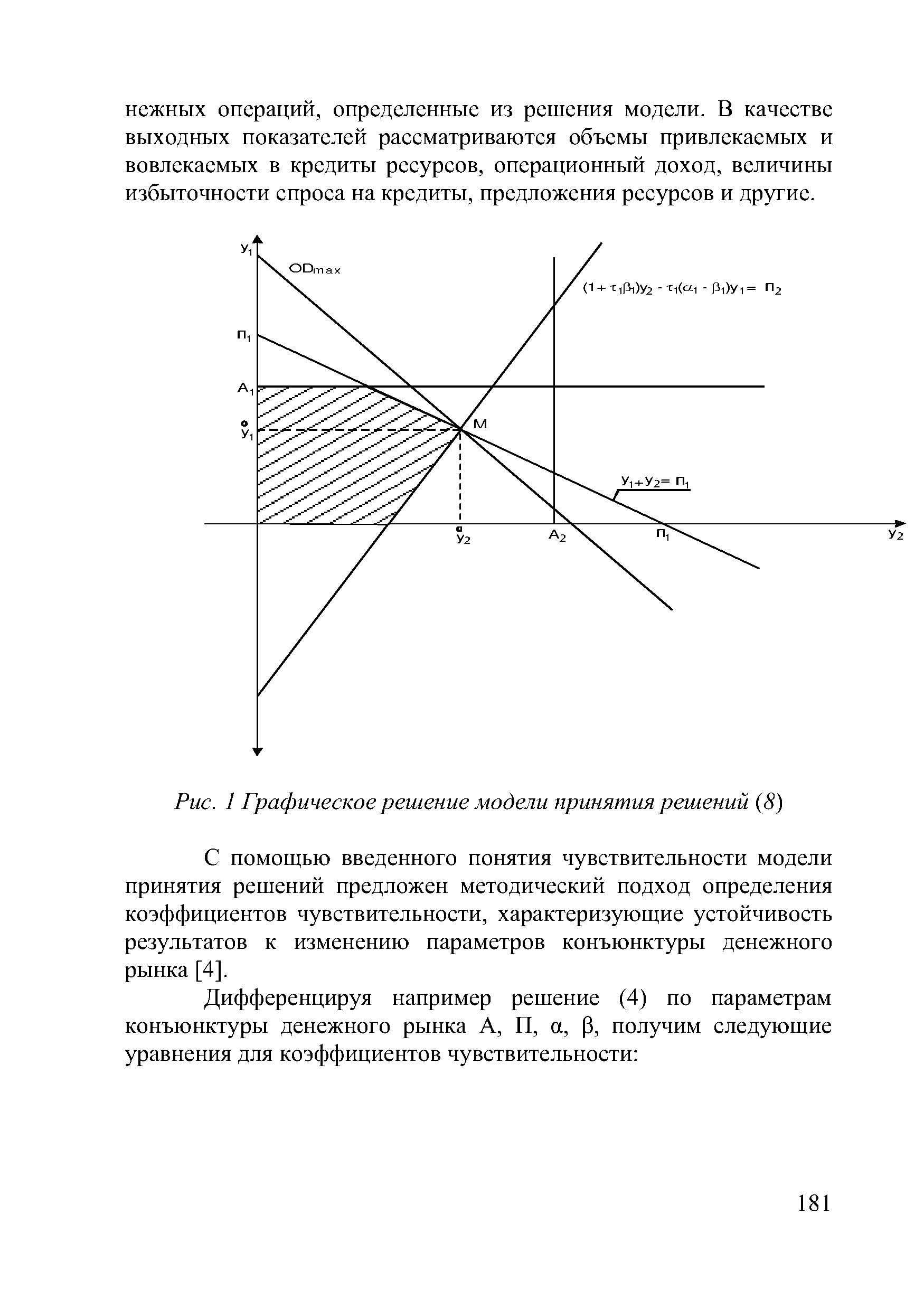 |
Графическое решение представлено на рис. 11.8. При цене Рй объем производства фирмы составит ( 0. При таком объеме предельный доход равен предельным издержкам, а минимальные средние валовые издержки равны рыночной цене, экономическая прибыль равна нулю. При таких условиях фирма удовлетворена объемом производства и размерами предприятия. [c.236]
Это позволяет получить удобный для управления набор графических решений для определения критического объема производства КБУ, соответствующего точке безубыточности, в виде эквидистантных кривых зависимости КБУ от относительной цены р при фиксированных значениях второго параметра — относи- [c.99]
На рис. 4.4 дана последовательность графического решения этой задачи (7-> 8 ->9). [c.158]
Для того чтобы сформировать интуитивное представление о том, как может меняться решение задачи линейного программирования при изменении параметров, полезно получить и проанализировать графическое решение нашего первого "игрушечного" примера об оптимальном плане мебельного цеха, а также познакомиться с понятием двойственности задач линейного программирования. [c.55]
Графическое решение задачи об оптимальном плане выпуска продукции мебельного цеха [c.56]
Графическое решение задачи об оптимальном плане мебельного цеха [c.57]
Следует заметить, что подобное графическое решение очень трудно провести для задач с тремя переменными решения. В этом случае область допустимых планов представляет собой многогранник сложной формы в 3-мерном пространстве. Что же касается задач с числом переменных более трех, то графически изобразить область допустимых планов вообще нельзя, поскольку это многогранник в многомерном пространстве. [c.59]
Таким образом, графическое решение никоим образом нельзя рассматривать как практический метод решения задач линейного программирования. Однако проведенный графический анализ дает [c.59]
Первый шаг к графическому решению состоит в том, чтобы начертить функцию инвестиции в координатах q— i. Для. этой цели мы рассчитаем значения доходности, исходя из [c.13]
Оптимальное значение х находится аналитическим йот графическим решением данного уравнения. В рассматриваемом примере минимальным затратам суммарного оперативного времени на изготовление единицы продукции отвечает глубина пооперационного разделения труда, достигаемая при расчленении производственного процесса на 8 операции. При анализе рациональности сложившихся форм кооперации труда следует ориентироваться на основные проблемы в этой области оптимизацию численного, квалификационного в профессионального состава бригад, максимальное уплотнение рабочего дня путем выбора оптимального варианта распределения работ между исполнителями. Оптимальный численный, квалификационный и профессиональный состав бригады должен соответствовать квалификационной структуре гтрат рабочего времени по обслуживанию установки. Сочетание действий исполнителей я работы машин должно обеспечивать минимальную длительность производственного цикла. Она достигается при параллельном выполнении операций, составлявших частичный производственный процесс. [c.12]
Графическое решение может быть заменено числовым или алгебраическим. Кстати, это все равно придется сделать, если объем сбыта является производным от более чем одной переменной комплекса маркетинга9. [c.592]
Д5Ягв = 200000 - 160000 = +40000 млн руб. Покажем графическое решение задачи в разных вариантах (рис. 6.2). [c.119]
Со временем графическое решение этикетки выходит из моды и требует обновления. С 1890-х гг. этикетку мыла Ivory переделывали 18 раз, включая кардинальное изменение размера и рисунка букв. Этикетка газированного напитка Orange rush существенно изменилась (новые символы, насыщенные глубокие цвета) после того, как конкуренты стали изображать на этикетках свежие фрукты, что привело к увеличению объемов продаж. [c.536]
Графическое решение рассматриваемой задачи приведено на-фиг. 22 [106]. На этом графике изображены себестоимость с, изготовления изделия из прежнего материала (сг = onst, поскольку она не зависит от цены нового материалн) и себестоимость с2 при изготовлении изделия из нового материала в функции от цены этого материала [ 2=f(s2)]. Точка пересечения прямых с2 и -L показывает, при какой цене нового материала применение его в данном назначении становится рентабельным. [c.111]
Если имеется графическая модель, где у = узад, К = Кзад, то на этом графике на горизонтальной оси р находим точку, где р = Рзад. В этой точке р = Рзад восстанавливаем перпендикуляр (вертикальную прямую) до пересечения с прямой К = Кзад. Из этой точки опускаем перпендикуляр на вертикальную ось относительной прибыли Р. Определяем значение Р. Зная Р, вычисляем абсолютное значение прибыли Р = Р Зг Порядок графического решения дан на рис. 4.4 (последовательность 1 -> 2 - 3). [c.157]
Определение порога прибыли (ТКОП) осуществляется двумя способами планирования или одним из них. Первый способ известен под названием графика критического объема производства (break-even- hart). Второй способ базируется на алгебраическом решении. Рассмотрим указанные способы. Первый способ предусматривает графическое решение. По горизонтали показывают объем продукции (в натуральном или стоимостном выражении), который регламентирован наличием производственных мощностей у предприятия. По вертикали показывают постоянные и переменные затраты, т. е. полную себестоимость регламентированного объема продукции и прибыль, в сумме составляющие выручку от продаж. На графике видно, что разность между выручкой от продаж и переменными расходами или сумма постоянных затрат и прибыли представляет собой маржинальный доход предприятия. [c.179]
Ее графическое решение представлено на рис. 1.21. Ради облегчения восприятия четыре прямые обозначены номерами (1) —(4). Прямая (1) — это прямая l,00xi + 0,25х2 = 5,00 (ограничение по веществу Н). Она проходит, как и показано на рисунке, через точки (5,0) на оси абсцисс и (0, 20) на оси ординат. Обратите внимание, что допустимые значения параметров (хь х2) лежат выше прямой (1) или на ней, в отличие от ранее рассмотренных случаев в предыдущей производственной задаче. [c.166]
Смотреть страницы где упоминается термин Графическое решение
: [c.380] [c.292] [c.260] [c.266] [c.56] [c.158]Смотреть главы в:
Количественные методы анализа хозяйственной деятельности -> Графическое решение
