Кроме балансового в плановой работе используются и другие методы экономического анализа и синтеза, прямого счета, расчета по факторам, экстраполяции и итерации, экономико-математические методы (линейного программирования, динамического программирования, матричный и др.), метод экономико-математического моделирования. [c.72]
Модели оптимизации экономики имеют целью добиться наибольшей результативности (эффективности) использования имеющегося потенциала и ресурсов. Любая экономико-математическая модель — это воспроизведение связей между экономическими явлениями и процессами. Критерии оптимального плана могут быть разными, поэтому в общей форме подразумевается оптимальное сочетание цели и средств социалистического производства за счет интенсивного использования всех имеющихся возможностей. Целевая функция и ограничения выражаются в математическом виде, и решение их методами линейного программирования позволяет найти оптимальный вариант. [c.73]
В условиях серийного производства при изготовлении на одном оборудовании нескольких видов продукции число машино-смен, нужное для изготовления каждого вида, не равно общему возможному числу смен в месяц. Поэтому возникает необходимость решить вопрос об отборе номенклатуры продукции, закрепляемой за данным оборудованием, и определить, какую продукцию, в какие дни и смены следует изготовлять. Для этого могут быть использованы методы линейного программирования, а также целочисленное программирование. [c.199]
Известны следующие методы линейное программирование, динамическое программирование, теория игр и массового обслуживания, матричный метод затраты — выпуск и др. Наибольшее распространение получили методы линейного программирования. Задачи, решаемые с помощью этих методов, носят экстремальный характер. Результатом решения является определение максимума или минимума какой-то целевой функции, в качестве которой может приниматься прибыль, выработка товарной продукции, себестоимость и др. Выбор целевой функции зависит от пели задачи. В связи с переходом на новые условия планирования для предприятия в целом более целесообразна постановка задачи на максимум прибыли (П). Математически такая задача формулируется следующим образом [c.127]
С помощью методов линейного программирования определяют оптимальную производственную программу, оптимальные варианты смешения (компаундирования) товарных нефтепродуктов, оптимальную технологическую схему, наилучший вариант использования сырья и др. В нефтепереработке наибольшее распространение получило определение методами линейного программирования оптимальной производственной программы. [c.127]
Для большей сбалансированности всех разделов плана используют также матричные модели затраты — выпуск по форме, аналогичной межотраслевому балансу. Хотя матричная модель не включает всех разделов плана, она позволяет достигнуть четкой сбалансированности его основных разделов. Оптимального варианта такая модель не дает, поэтому использовать ее. можно в сочетании с моделью линейного программирования оптимального варианта производственной программы. [c.128]
Для оптимизации производственной программы разработан ряд статических экономико-математических моделей, основанных на методах линейного программирования и с достаточной точностью описывающих возможности нефтеперерабатывающего предприятия. Критериями оптимальности служат максимум прибыли, минимум затрат, максимум выработки товарной про- [c.162]
Возможности увеличения прибыл т и рентабельности производства еще больше возрастают npi. использовании методов линейного программирования для разработки производственной программы предприятия. В этом случае имеется возможность увеличить прибыль предприятия не только в результате более рационального смешения отдельных компонентов при приготовлении товарных нефтепродуктов, но и в результате снижения себестоимости целевой продукции при выборе оптимальных вариантов работы технологических установок. [c.296]
Рациональное размещение новых предприятий и производств существенно влияет на повышение эффективности производства. Выбор оптимального варианта осуществляют с учетом экономических, социальных и экологических факторов с применением экономико-математических методов, основанных на нахождении минимума приведенных затрат на выпуск продукции вновь строящихся предприятий. Для выбора оптимального варианта размещения предприятий широко используют модели транспортной задачи, решаемой методами линейного программирования. [c.328]
МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ применяют для определения оптимального способа распределения дефицитных ресурсов при наличии конкурирующих потребностей. Согласно опросу журналом Форчун вице-президентов по производству из 500 фирм, модели линейного программирования и управления запасами пользуются в промышленности наибольшей популярностью. Линейное программирование обычно используют специалисты штабных подразделений для разрешения производственных трудностей. Некоторые типичные применения этого метода в управлении производством перечислены в табл. 8.1. [c.232]
Нижеследующий пример иллюстрирует простую ситуацию, в которой для принятия решения следует воспользоваться моделью линейного программирования. Управляющий производством должен решить, сколько галлонов краски каждого из трех ее типов следует производить, чтобы получить наивысшую прибыль. На решение налагается несколько ограничений [c.232]
Задача проиллюстрирована рис. 8.3. С помощью модели линейного программирования управляющий может определить, какое количество краски каждого типа производить при известных запасах реагентов и имеющемся резерве времени работы оборудования, а также с учетом вклада в прибыль краски каждого типа. Не имея такой модели, крайне сложно принять оптимальное решение даже в сравнительно простой ситуации. [c.232]
Имитация используется в ситуациях, слишком сложных для математических методов типа линейного программирования. Это может быть связано с чрезмерно [c.232]
Т а б л 3i ц а 8.1. Типичные варианты применения линейного программирования в управлении производством [c.233]
| Рис. 8.3. Модель линейного программирования (линейное программирование применяется для решения задач с несколькими переменными, как например, задачи об ассортименте красок в тексте). | 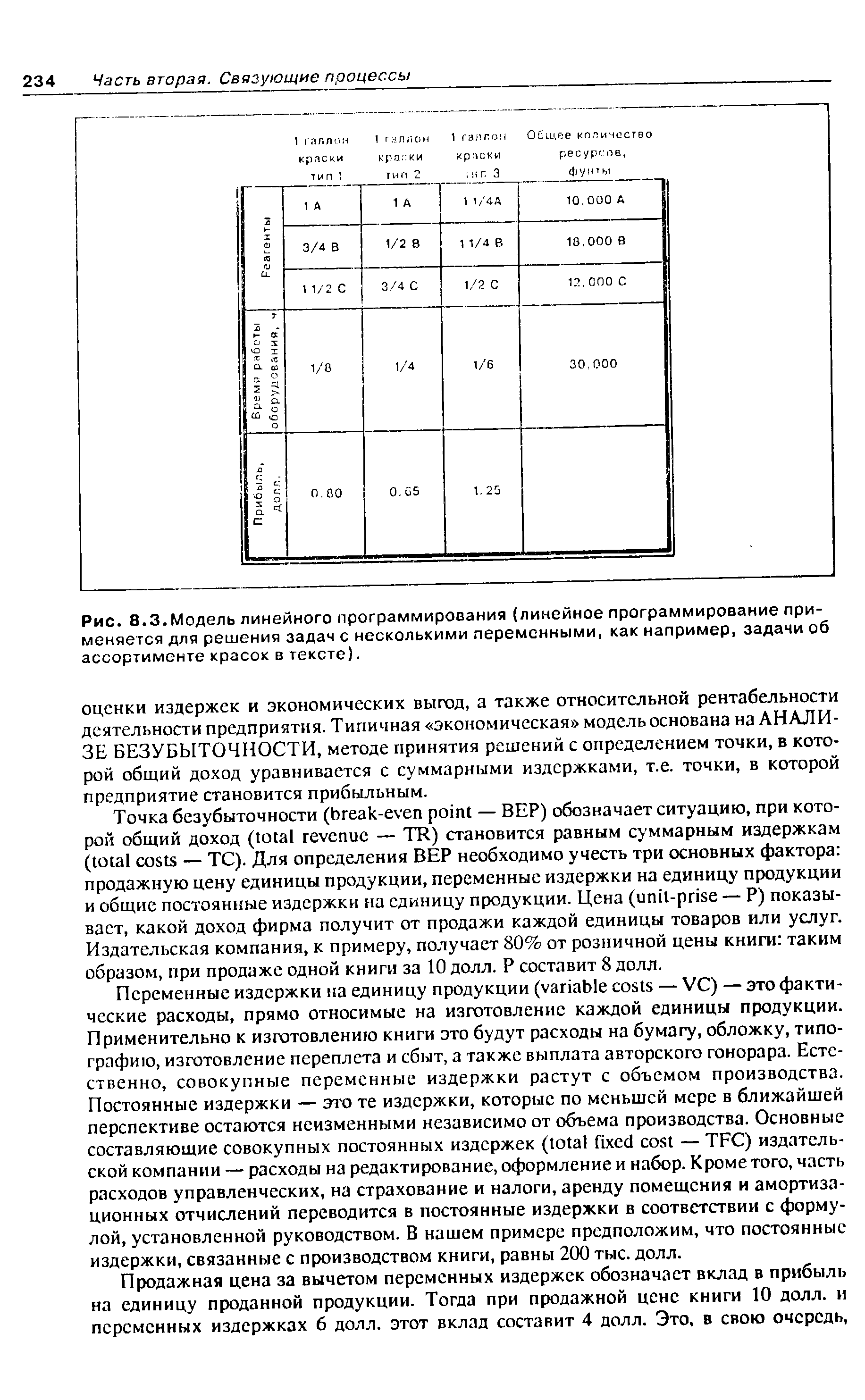 |
А. С. Астахов, восходящая в то время звезда экономики горной промышленности, в своих ранних работах (1966, 1968, 1973) применил методы линейного программирования в горной промышленности и вплотную подошел к парадоксу дисконтирования, но пропустил его открытие. [c.62]
В ряде случаев проникнуть в изучаемые хозяйственные явления и процессы известными традиционными способами невозможно, необходимы иные приемы анализа. Поэтому в настоящее время при анализе сложных производственно-хозяйствен ных явлений все более широко применяются математические методы. Наибольшее распространение получили такие из них, как линейное программирование, математическая статистика, теория вероятности, экономическая кибернетика и др. [c.19]
Линейное программирование используется при анализе напряженности плановых заданий, рациональной организации пе- [c.19]
Преимущество линейного программирования состоит в том, что оно позволяет использовать при анализе деятельности пред приятия различные сочетания математического обеспечения, что позволяет найти наиболее оптимальный вариант для раскрытия изучаемого объекта, не прибегая при этом к нескольким приемам изучения. [c.20]
Итак, для нахождения оптимальной производственной программы необходимо такое решение системы многих уравнений с многими неизвестными, при котором критерий (целевая функция) достигает оптимума. Система уравнений и неравенств (24.1) — (24.5), (24.7) обладает следующим свойством она линейна относительно неизвестных. Это означает, что неизвестные входят в уравнения, неравенства и критерий лишь в первой степени и что отсутствуют произведения неизвестных. Методом решения подобных задач, которые носят название задач линейного программирования, служит так называемый симплекс-метод. Симплекс-метод изложен в целом ряде книг. Ограничимся лишь его технико-экономической интерпретацией. [c.413]
Существует хотя бы два допустимых плана. В этом случае, как доказывается в теории линейного программирования, существует бесчисленное множество допустимых планов. Это означает, что все требования внешней среды, все плановые лимиты вышестоящих организаций могут быть выполнены, причем существует возможность рационального использования внутренних производственных ресурсов, например возможность выбора режимов эксплуатации отдельных установок. Именно в данном случае удается оптимизировать работу предприятия за счет выбора рациональных (с точки зрения всего предприятия) режимов эксплуатации отдельных установок, выбора рационального распределения входных и промежуточных материальных потоков. [c.414]
На предприятиях химической и нефтехимической промышленности, которые отличаются своими специфическими особенностями, оптимизация текущих планов (производственной программы) может быть достигнута в подавляющем большинстве случаев в рамках ЭММ линейного программирования. При этом подразумевается, что решение задачи оптимизации производственной программы предприятия осуществляется на основе информации о его производственных возможностях (набор вариантов). [c.421]
Рассматриваемая задача решается с помощью экономико-математических методов, в частности, линейного программирования. Целевая функция задачи выглядит при этом следующим образом [c.17]
Наиболее распространенным методом решения важных практических задач планирования и управления является линейное программирование. С помощью симплекс-метода решаются задачи планирования производственной программы предприятия, объединения, способствующие получению максимального эффекта при ограниченных материальных и трудовых ресурсах. Распределительный метод линейного программирования позволяет выбрать оптимальные варианты планов транспортных перевозок решать задачи по оптимизации планов загрузки оборудования и др. [c.78]
Рассмотрим постановку задачи определения оптимальной производственной программы отрасли методами линейного программирования. [c.96]
Математическая модель задачи оптимального компаундирования представляет собой частный случай общей задачи линейного программирования о смесях. При построении математической модели процесса необходимо учитывать те же условия и ограничения, которыми руководствуются при объемных расчетах компаундирования, например подчиненность компонентов правилу аддитивности, приемистость их к ГЭС, технические условия на нефтепродукты согласно ГОСТ, ресурс каждого компонента и др. [c.134]
Линейная алгебра лежит в основе методов линейного программирования. С помощью этих методов могут быть решены следующие задачи рассчитана производственная мощность предприятия, цехов, участков разработаны производственные задания цехам, участкам и др. [c.153]
Задачи линейного программирования направлены на нахождение способа эффективного использования или распределения ограниченных ресурсов для достижения поставленных целей. Условия задачи записывают в виде системы линейных уравнений или неравенств (системы ограничений), а результат в виде целевой функции, являющейся суммой произведений найденных значений переменных на присваиваемые им показатели эффективности. Искомыми неизвестными величинами могут быть, например, различные виды оборудования. Коэффициенты при неизвестных в системе ограничений являются заданными постоянными числами и выражают удельные затраты. Коэффициенты при неизвестных в целевой функции — также постоянные величины. Они могут представлять собой себестоимость, цену оборудования, материалов, степень загрузки оборудования и т. п. Свободные члены в ограничениях — это величины тех или иных ресурсов, которые нужно распределить оптимальным образом (запасы материалов, фонды времени работы оборудования). [c.153]
После того, как задача сформулирована в терминах линейного программирования, решение ее состоит в применении того или иного расчетного алгоритма. Наиболее распространенными методами решения задач линейного программирования являются симплексный (или метод последовательного улучшения плана), распределительный и индексный. Существует также ряд приближенных методов решения, разработанных для отдельных видов задач (пример решения задачи методом линейного программирования дан ниже). [c.153]
Применение методов линейного программирования при планировании эксплуатационных затрат на строительство скважин. В этом случае целевая функция задачи имеет следующий вид [c.156]
Наиболее распространены методы линейного программирования. Результат их решения (как было сказано) — определение максимума или минимума какой-то целевой функции, в качестве которой принимается прибыль, затраты на производство, выработка продукции и др. Выбор целевой функции зависит от цели задачи. В современных условиях более целесообразна постановка задачи на максимум прибыли (П). Математически такая задача формулируется следующим образом [c.18]
С помощью линейного программирования в основном определяется его производственная программа. [c.18]
Применение метода линейного программирования для выбора вариантов смешения компонентов в товарные бензины значительно ускоряет все расчеты и дает возможность получить наиболее рентабельный план производства, предусмотрев увеличение выпуска бензинов с повышенной октановой характеристикой. Это, в свою очередь, дает возможность [c.73]
С помощью метода линейного программирования решают задачи производственного планирования составление оптимальной программы выпуска продукции при заданных ресурсах- оптимальной загрузки оборудования и др. [c.146]
Транспортную задачу линейного программирования успешно применяют для планирования перевозок. Другая разновидность ее позволяет выбрать наилучшее местоположение для вновь создаваемых предприятий. [c.146]
В строительств в настоящее время чаще всего применяют простейшие модели оптимального планирования — так называемые модели линейного программирования, которые имеют глубоко разработанные и широко проверенные на практике методы решения. В целом линейное программирование объединяет теорию и методы решения определенного класса задач, в которых требуется найти совокупность переменных, удовлетворяющих линейным ограничениям, и максимизирующую (минимизирующую) линейную целевую функцию этих переменных. [c.24]
Характерным и наиболее распространенным примером задачи линейного программирования является известная транспортная 24 [c.24]
Одним из наиболее известных методов является система Аккорд (автоматизация контроля и координации оптимальных режимов деятельности). Оптимизация рабочей силы в этой системе выполняется по программе Дельта . Идея алгоритма этой программы сводится к использованию метода линейного программирования на сети. Можно отметить достаточную строгость применяемого в этом методе математического аппарата. Недостаток этого метода заключается в том, что оптимизация проводится без учета механизации работ (путем добавления или изменения одних рабочих). [c.47]
Зависимость отдельных составляющих целевой функции от числа пунктов разгрузки, включенных в какой-либо вариант внешнего транспортного обеспечения и условно рассматриваемых как непрерывные функции в области целочисленных величин числа пунктов разгрузки пгв, представлена на рис. 27. Как видно из рисунка, с увеличением числа пунктов разгрузки возрастают суммарные затраты на их организацию и уменьшаются транспортные расходы по доставке труб к месту работ. Следовательно, целевая функция как сумма указанных составляющих имеет экстремум при некотором значении числа пунктов разгрузки. Учитывая нелинейную зависимость функционала и его отдельных составляющих от числа вводимых пунктов разгрузки и искомых переменных, для решения поставленной задачи не могут быть применены классические методы математического программирования (например,. линейного). Как известно из курса высшей математики, математическое программирование — область математики, разрабатывающая теорию и методы решения многомерных экстремальных задач с ограничениями, т. е. задач на экстремум функции многих переменных с ограничениями на область изменения этих переменных. Само название программирование взято из линейного программирования, где оно обычно обозначает распределение наилучшим образом ограниченных ресурсов для достижения поставленных целей. Следовательно, термин программирование здесь можно заменить термином планирование . [c.145]
Оптимизация режима работы отдельных технологических установок еще не обеспечивает получения адекватного эффекта в целом по заводу. Ведь все технологические установки связаны единой технологической цепочкой. Поэтому оптимизация работы отдельных технологических установок лишь первый этап работы по повышению эффективности использования средств труда. Вторым этапом этой работы является составление оптимальной производственной программы завода с применением методов линейного программирования. В этом случае [c.108]
В настоящее время с использованием линейного программирования разрабатываются математические модели оптимальной производственной программы, оптимальной загрузки оборудования, оптимального смешения нефтепродуктов, производительности труда. Это оптимальное решение применяют в качестве модели. Путем сравнения фактических результатов с показателями модели определяют отклонения и их причины с целью разработки мероприятий по приближению к оптимальной модели. [c.26]
Нефтеперерабатывающая и нефтехимическая промышленность относится к числу отраслей, где математические методы стали использоваться значительно раньше, чем в других отраслях. Основу этих методов составило линейное программирование. ЦЭМИ АН СССР совместно с отраслевыми институтами разработали следующие модели [c.156]
Ограничивающими условиями служат производительности участков сети и объемы добычи газа. Задача решается на ЭВМ методами линейного программирования. В результате расчета на печать выдаются объемы транспортировки газа по участкам газотранспортной сети, уточненный объем поступления газа из газодобывающих районов, а также возможные объемы недопо-дачи газа потребителям (с указанием узлов, где возможна недо-подача). После выдачи на печать весь этот массив данных (состоящий из номеров переменных и соответствующих численных значений) запоминается в памяти ЭВМ и используется на втором этапе расчета для формирования плана транспорта газа по объединениям Министерства. При формировании плана транспорта газа используется также информация о составе газотранспортного объединения. Эта информация содержит перечень участков газопроводов, принадлежащих данному объединению. В особую группу выделены участки, по которым осуществляется поступление газа данному объединению, а также передача соседним объединениям. Для каждого участка, включенного в такую группу, указывают наименование и код объединения, поставляющего или получающего газ. [c.191]
Применение метода линейного программирования для выбо-р вариантов смешения компонентов в товарные бензины позволяет значительно ускорить расчеты и выбрать оптимальный план производства, предусмотрев увеличение выпуска бензинов с повышенной октановой характеристикой. Это в свою очередь дает возможность при неизменной себестоимости производства бензиновых компонентов увеличить шработку чистой и товарной продукции в стоимостном выражении, снизить затраты па [c.294]
Смотреть страницы где упоминается термин Линейное программирование
: [c.219] [c.687] [c.98] [c.115]Смотреть главы в:
Финансовый анализ - методы и процедуры -> Линейное программирование
Количественные методы анализа хозяйственной деятельности -> Линейное программирование
Менеджмент -> Линейное программирование
Операционный менеджмент -> Линейное программирование
Менеджмент в техносфере -> Линейное программирование
Количественные методы в финансах -> Линейное программирование
Организация и планирование кислородного производства -> Линейное программирование
Математические методы моделирования экономических систем Изд2 -> Линейное программирование
Математические исследования операций в экономике -> Линейное программирование
Экономика, организация и планирование строительства (1987) -- [ c.33 , c.337 ]
Количественные методы анализа хозяйственной деятельности (1999) -- [ c.260 , c.307 ]
Принципы корпоративных финансов (1999) -- [ c.0 ]
Организация, планирование и управление энергомашиностроительным предприятием (1977) -- [ c.232 , c.235 , c.305 ]
Экономико-математический словарь Изд.5 (2003) -- [ c.170 ]
Популярный экономико-математический словарь (1973) -- [ c.120 ]
Справочник по математике для экономистов (1987) -- [ c.185 ]
