Во многих случаях в реальной практике действует не один, а несколько лимитирующих факторов. Задача максимизации прибыли или минимизации затрат решается здесь с помощью линейного программирования. Модели линейного программирования в управленческом учете будут рассмотрены далее (см. главу 8). [c.219]
В ряду задач линейного программирования модель задачи О. и. п. м. является относительно сложной. В ней много переменных (их число равняется произведению числа станков на число обрабатываемых изделий), а в числе ограничивающих условий фигурируют неравенства, в к-рые неизвестные (х) входят с определенными коэффициентами. Такого рода ограничения усложняют решение задачи по сравнению, напр., с транспортной задачей, где все переменные в уравнениях-ограничениях имеют коэффициент, равный 1 (см. Перевозок план оптимальный). [c.113]
Модели оптимизации экономики имеют целью добиться наибольшей результативности (эффективности) использования имеющегося потенциала и ресурсов. Любая экономико-математическая модель — это воспроизведение связей между экономическими явлениями и процессами. Критерии оптимального плана могут быть разными, поэтому в общей форме подразумевается оптимальное сочетание цели и средств социалистического производства за счет интенсивного использования всех имеющихся возможностей. Целевая функция и ограничения выражаются в математическом виде, и решение их методами линейного программирования позволяет найти оптимальный вариант. [c.73]
Для большей сбалансированности всех разделов плана используют также матричные модели затраты — выпуск по форме, аналогичной межотраслевому балансу. Хотя матричная модель не включает всех разделов плана, она позволяет достигнуть четкой сбалансированности его основных разделов. Оптимального варианта такая модель не дает, поэтому использовать ее. можно в сочетании с моделью линейного программирования оптимального варианта производственной программы. [c.128]
Для оптимизации производственной программы разработан ряд статических экономико-математических моделей, основанных на методах линейного программирования и с достаточной точностью описывающих возможности нефтеперерабатывающего предприятия. Критериями оптимальности служат максимум прибыли, минимум затрат, максимум выработки товарной про- [c.162]
Рациональное размещение новых предприятий и производств существенно влияет на повышение эффективности производства. Выбор оптимального варианта осуществляют с учетом экономических, социальных и экологических факторов с применением экономико-математических методов, основанных на нахождении минимума приведенных затрат на выпуск продукции вновь строящихся предприятий. Для выбора оптимального варианта размещения предприятий широко используют модели транспортной задачи, решаемой методами линейного программирования. [c.328]
МОДЕЛЬ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ применяют для определения оптимального способа распределения дефицитных ресурсов при наличии конкурирующих потребностей. Согласно опросу журналом Форчун вице-президентов по производству из 500 фирм, модели линейного программирования и управления запасами пользуются в промышленности наибольшей популярностью. Линейное программирование обычно используют специалисты штабных подразделений для разрешения производственных трудностей. Некоторые типичные применения этого метода в управлении производством перечислены в табл. 8.1. [c.232]
Нижеследующий пример иллюстрирует простую ситуацию, в которой для принятия решения следует воспользоваться моделью линейного программирования. Управляющий производством должен решить, сколько галлонов краски каждого из трех ее типов следует производить, чтобы получить наивысшую прибыль. На решение налагается несколько ограничений [c.232]
Задача проиллюстрирована рис. 8.3. С помощью модели линейного программирования управляющий может определить, какое количество краски каждого типа производить при известных запасах реагентов и имеющемся резерве времени работы оборудования, а также с учетом вклада в прибыль краски каждого типа. Не имея такой модели, крайне сложно принять оптимальное решение даже в сравнительно простой ситуации. [c.232]
| Рис. 8.3. Модель линейного программирования (линейное программирование применяется для решения задач с несколькими переменными, как например, задачи об ассортименте красок в тексте). | 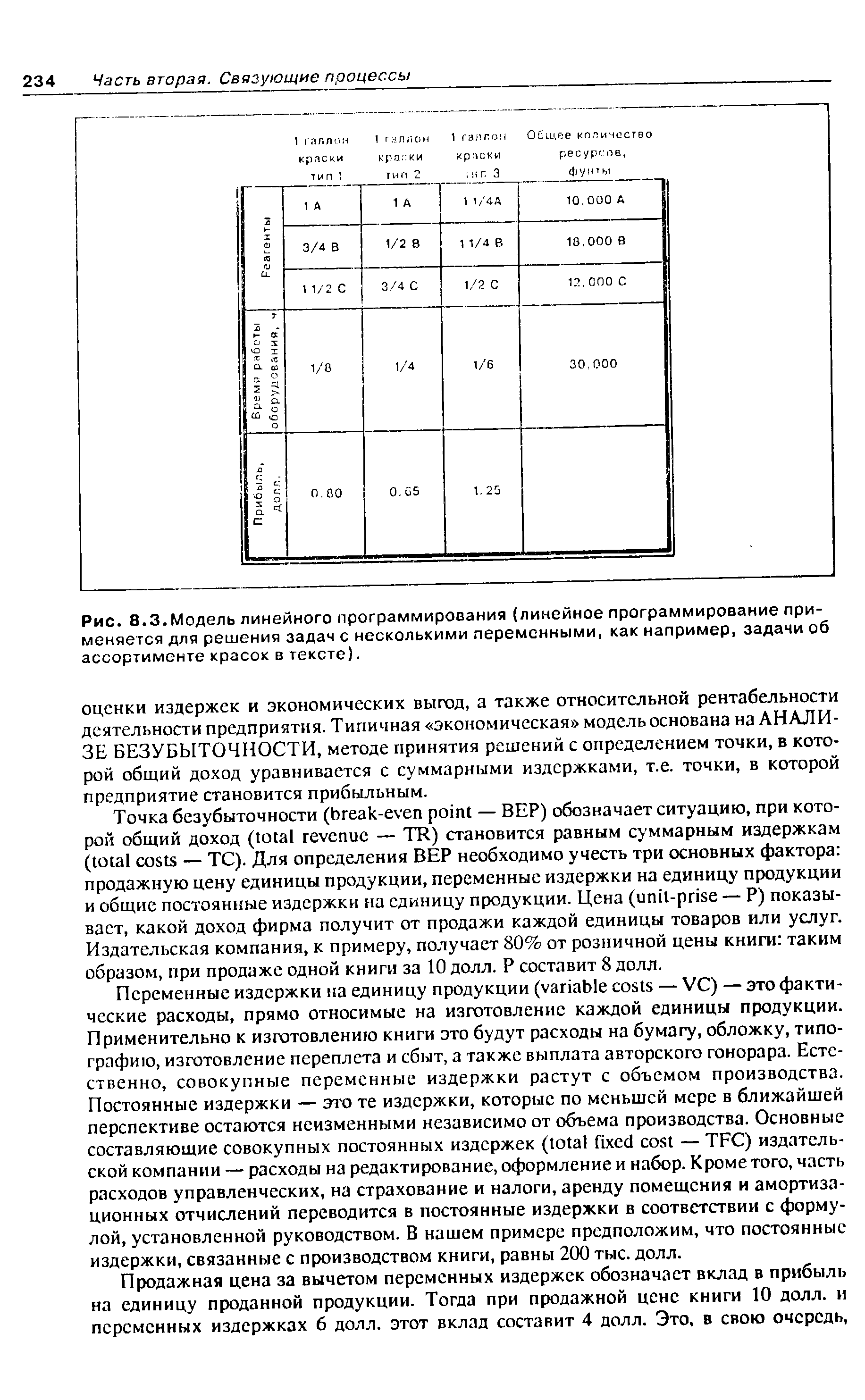 |
Математическая модель задачи оптимального компаундирования представляет собой частный случай общей задачи линейного программирования о смесях. При построении математической модели процесса необходимо учитывать те же условия и ограничения, которыми руководствуются при объемных расчетах компаундирования, например подчиненность компонентов правилу аддитивности, приемистость их к ГЭС, технические условия на нефтепродукты согласно ГОСТ, ресурс каждого компонента и др. [c.134]
В строительств в настоящее время чаще всего применяют простейшие модели оптимального планирования — так называемые модели линейного программирования, которые имеют глубоко разработанные и широко проверенные на практике методы решения. В целом линейное программирование объединяет теорию и методы решения определенного класса задач, в которых требуется найти совокупность переменных, удовлетворяющих линейным ограничениям, и максимизирующую (минимизирующую) линейную целевую функцию этих переменных. [c.24]
В настоящее время с использованием линейного программирования разрабатываются математические модели оптимальной производственной программы, оптимальной загрузки оборудования, оптимального смешения нефтепродуктов, производительности труда. Это оптимальное решение применяют в качестве модели. Путем сравнения фактических результатов с показателями модели определяют отклонения и их причины с целью разработки мероприятий по приближению к оптимальной модели. [c.26]
Нефтеперерабатывающая и нефтехимическая промышленность относится к числу отраслей, где математические методы стали использоваться значительно раньше, чем в других отраслях. Основу этих методов составило линейное программирование. ЦЭМИ АН СССР совместно с отраслевыми институтами разработали следующие модели [c.156]
К задачам прямой обработки данных принято относить такие автоматизируемые планово-экономические задачи, реализация которых не требует применения специальных математических методов решения. В отличие от задач, базирующихся на экономико-математических моделях, в решении которых используются методы матричной алгебры, линейного программирования, математической статистики и другие, задачи прямой обработки данных сводятся к обработке на ЭВМ больших массивов информации при помощи простейших алгоритмов сортировки, табулирования, агрегирования и других, а также преобразований по элементарным формулам (например, потребность в данном ресурсе на производство какой-либо продукции определяется как произведение соответствующей удельной нормы расхода на объем производства этой продукции). [c.126]
Чтобы решить экономическую задачу одним из методов линейного программирования, необходимо ее условие выразить в математической форме или составить ее математическую модель. [c.33]
Основной математической моделью, используемой для составления оптимальных планов поставок и грузовых перевозок, является транспортная задача линейного программирования. [c.284]
В основу математической модели может быть заложена производственно-транспортная модель линейного программирования. Первый этап этой задачи, предусматривающий обеспечение минимальных суммарных эксплуатационных издержек на транспорт и хранение при рациональном прикреплении потребителей в условиях заданного грузооборота, формулируется в следующем виде. [c.81]
В данной статье предложена адекватная математическая модель распределения временно свободных денежных средств предприятия, найдена декомпозиция исходной задачи, сводящая ее решение к решению двух подзадач. Первую предложено решать на основе метода ветвей и границ (это позволит рассмотреть все допустимые множества исходов, удовлетворяющие ожиданиям инвестора), а вторую подзадачу (получение оптимального портфеля инвестиций в активы на заданном множестве исходов) - методом линейного программирования. [c.120]
Решение широкого класса планово-экономических задач основывается на моделях линейного программирования. В наибольшей степени методы линейного программирования получили применения в расчетах оптимальной производственной программы НПЗ [1 — 2]. В, общем виде задача оптимизации производственной программы нефтеперерабатывающего предприятия записывается в следующем виде / [c.96]
Формирование матрицы коэффициентов модели линейного программирования. [c.167]
Реинжиниринг стратегических бизнес-процессов компании обусловлен новыми тенденциями развития общества и экономики, предъявляющими жесткие требования к задачам управления создаваемыми, действующими и развивающимися корпорациями, так как конкурентоспособное функционирование корпораций становится невозможным без реорганизации стратегических бизнес-процессов, представляющей собой совокупность стратегических мероприятий по комплексному совершенствованию системы управления, технологий деятельности, внутреннего и внешнего взаимодействия. Проведение реинжиниринга стратегических бизнес-процессов потребовало детального анализа стратегических моделей. Таким образом, центр тяжести смещается от ключевой верификации оценки качества бизнес-процесса к интегрированной функциональности статистический анализ и представление результатов в наглядном виде линейное программирование и вычисление наиболее эффективных комбинаций ресурсов функционально-стоимостной анализ динамическое моделирование, в том числе анимационными средствами. [c.77]
Поскольку описываемые здесь модели планирования экономических объектов предназначены для выбора наилучшего плана, под которым обычно понимается план, оптимальный в смысле некоторого критерия, то модели стараются сформулировать в таком виде, чтобы воспользоваться уже существующими методами решения задач оптимизации. Наиболее развитыми методами решения оптимизационных задач являются методы линейного программирования, т. е. методы оптимизации на основе моделей, состоящих из линейных равенств и неравенств, причем критерий оптимизации является линейной функцией от переменных задачи. Это — одна из причин того, что линейные модели получили наиболее широкое распространение в практических экономических расчетах. [c.150]
Конечно, хорошего развития методов линейного программирования недостаточно для широкого распространения линейных моделей экономических объектов—более существенной причиной является то, что линейные модели оказались во многих случаях довольно реалистичными. [c.150]
Легко заметить, что эта задача отличается от транспортной задачи лишь наличием величин Кц в ограничениях одного из типов (отсюда и одно из названий такой задачи — -задача). Для обобщенной транспортной задачи также разработаны алгоритмы решения, более эффективные, чем алгоритмы решения общей задачи линейного программирования. Транспортная задача проще обобщенной транспортной задачи с точки зрения алгоритма ее решения с помощью ЭВМ, а обобщенная транспортная задача проще общей задачи линейного программирования. При построении моделей их стараются сформулировать так, чтобы свести проблему к возможно более простой задаче. Конечно, такое сведение не должно осуществляться за счет искажения существенных черт изучаемой экономической системы. [c.152]
Заметим, что во втором варианте транспортной задачи с открытой моделью потребитель, спрос которого не будет удовлетворен, выбирается в соответствии с затратами на перевозку грузов. Такой подход верен не всегда часто приходится учитывать в критерии задачи потери потребителей от неполучения грузов, поэтому задача может уже не быть транспортной задачей и даже задачей линейного программирования вообще. Однако если эти потери пропорциональны величине недополученного груза, то критерий остается линейным и мы опять приходим к задаче линейного программирования. [c.156]
Поставленная здесь задача оптимального перспективного планирования свелась к задаче линейного программирования, причем довольно частного вида, очень близкого к транспортной задаче. Это большое достоинство модели такого типа, поскольку оказывается возможным решать задачу с большим числом пунктов производства и пунктов потребления. Кроме того, число параметров, входящих в модель, невелико, что облегчает сбор необходимой для расчетов информации. [c.171]
Проведенные нами изменения в модели не приводят к ее принципиальному усложнению. Задача оптимизации по-прежнему остается задачей линейного программирования, так что методы решения остаются прежними. Далее мы рассмотрим модификации модели, которые приведут к изменению типа задачи оптимизации. [c.173]
Новый этап в развитии методов экономико-математического моделирования начался в конце пятидесятых годов, когда появление вычислительной техники сделало многовариантные плановые расчеты на основе экономико-математических моделей реализуемыми по крайней мере принципиально. На развитие экономико-математических методов в это время большое влияние оказали работы Л. В. Канторовича, который в результате анализа некоторых задач планирования производства сформулировал новый важный для экономики класс математических задач, получивших название задач линейного программирования. В линейном программировании рассматривается вопрос о поиске среди всех допустимых решений, удовлетворяющих системе линейных равенств и неравенств, наилучшего (оптимального) решения, доставляющего максимум (или минимум) некоторому линейному критерию. В настоящее время линейное программирование является основным математическим методом анализа задач планирования производства. [c.16]
Легко заметить, что эта задача отличается от транспортной задачи лишь наличием величин X,j в ограничениях одного из типов (отсюда и одно из названий такой задачи — Х-задача). Транспортная задача проще обобщенной транспортной задачи, а обобщенная транспортная задача проще общей задачи линейного программирования. При построении математических моделей их стараются сформулировать так, чтобы свести проблему нахождения оптимального решения к возможно более простой задаче. [c.58]
Отметим, что методы линейного программирования исполь-дуются в настоящее время и для решения задач оптимизации в нелинейных моделях с нелинейными критериями. При этом осуществляется линеаризация соотношений модели в окрестности текущей точки и переход к новой точке с использованием результатов решения задачи линейного программирования. [c.58]
Только здесь переменные модели являются функциями времени. Если модель является многошаговой (например, типа (3.18), (3.21) — (3.23)), то в случае конечного числа шагов каждая функция времени описывается конечным числом скалярных величин, так что задачу оптимального управления удается свести к некоторой задаче оптимизации для специально сконструированной статической модели. Для ее решения можно применить упоминавшиеся ранее методы оптимизации. В частности, если динамическая модель является линейной, т. е. удовлетворяет соотношениям (3.18), (3.19), (3.23), (3.24), то можно применить методы линейного программирования. При этом задача линейного программирования благодаря своему происхождению имеет специальную форму, которой можно воспользоваться для упрощения расчетов. [c.58]
Помимо многочисленных технических вопросов, которые мы здесь рассматривать не будем ), приходится обычно решать одну принципиальную проблему — выбирать язык программирования. Для написания машинной программы у исследователя имеются две основные возможности выбрать универсальный язык программирования типа алгол, фортран, лисп и так далее либо остановиться на некотором специализированном языке. Так, для изучения математических моделей с помощью метода имитационных экспериментов разработаны специализированные языки динамо, симула и т. д. Кроме того, многие вычислительные системы, предназначенные для анализа моделей с помощью некоторых частных, но широко использующихся методов (например, методов линейного программирования), имеют свои собственные входные языки, являющиеся, по существу, специализированными языками программирования. [c.143]
Это — задача линейного программирования общего типа, т. е. рациональное распределение площадей с помощью модели (2.25) — (2.28) с критерием оптимизации (2.24) также может быть найдено с помощью систем линейного программирования. [c.172]
Анализ модели обычно производится с помощью методов и алгоритмов решения условных экстремальных задач или посредством статистич. моделирования. К числу наиболее широко применяемых в И. о. методов относится линейное программирование. Модели, приводящие к задачам линейного программирования, глубоко изучены, имеются эффективные алгоритмы и стандартные программы для ЭВМ, позволяющие решать задачи, содержащие тысячи ограничений и десятки тысяч переменных. Как правило, анализ моделей И. о. с помощью методов линейного программирования позволяет не только получить оптимальное решение, но и сделать онредел. качеств, выводы по организации операции. Эти выводы базируются на теории двойственности (объективно-обусловленные оценки) и принципах декомпозиции. Если целевая функция или ограничения модели исследуемой операции не могут быть достаточно точно описаны с помощью линейных функций, для её анализа используются др. методы математического программирования. Модели, в к-рых по смыслу операции все переменные или их часть могут принимать лишь конечное число различных значений, изучаются методами целочисленного или дискретного программирования, в частности, сюда относится большое число нла-ново-производств. операций, укладывающихся в схему т. н. задач календарного планирования и теории расписаний. Это задачи, связанные с нахождением последовательности обработки определ. числа изделий с помощью фиксированной системы машин, характеристики к-рых заданы. При этом должны быть соблюдены опродел. технологич. требования, к-рые по большей части выделяют допустимые последовательности обработки каждой детали на различных машинах. Задачи теории расписаний часто встречаются во внутризаводском планировании, особенно на мапшностроит. предприятиях. Модели, описывающие протяжённые во времени операции, цель к-рых достигается лишь с их окончанием, а осуществление может быть разделено на этапы, время начала и завершения к-рых должно быть согласовано, исследуются методами сетевого [c.74]
Основой для проведения расчетов по оптимизапи плана основного производства нефтеперерабатывающего предприятия является модель линейного программирования 11, 2]. Рассмотрим последовательность процесса формирования такой модели. [c.167]
Осуществление указанных этапов является достаточно трудоемкой задачей, причем по мере укрупнения и усложнения производства затраты времени на формирование и подготовку к решению зконсмико-математической модели прогрессивно возрастают. Кроме того, проведение каждого этапа связано с возможностью-возникновения значительного числа логических, арифметических и особенно механических ошибок, а формирование матрицы коэффициентов модели линейного программирования требует от исполнителей наличия определенных методических навыков. К другим-недостаткам4" существующей практики применения экономико-математических моделей в планировании следует отнести относительную разобщенность по месту выполнения отдельных этапов. Так, процесс отбора и формирования исходной информации о режимах и вариантах технологических процессов осуществляется при участии таких функциональных подразделений заводоуправления, как плановый и производственно-технический отделы, а все остальные этапы — в информационно-вычислительном центре. При этом применяемые способы передачи информации и ее качество нельзя признать удовлетворительными. Результатом является несогласованность, еще более усугубляющая указанные недостатки. [c.167]
Опыт, накопленный в области моделирования нефтеперерабатывающего предприятия, показывает, что проведение таких этапов, как формирование матрицы коэффициентов, кодирование ин- формации, перевод информации на машинные носители, связано с трудоемким процессом проверки и исправления ошибок. Поэтому наиболее рациональной представляется такая организация процесса моделирования, при которой без дополнительной ручной обработки первичные носители информации сразу переносились бы на машинные носители, а формирование матрицы козффициен-тоа модели линейного программирования осуществлялось бы с помощью ЭВМ в готовом для решения виде. [c.168]
Хотя матричная модель не включает всех разделов техпромфин-плана, она позволяет достигнуть четкой сбалансированности его основных разделов. Оптимального варианта такая модель не дает, поэтому использовать ее можно в сочетании с моделью линейного программирования оптимального варианта производственной программы. [c.89]
Графическим методом можно решать задачи линейного программирования с любым количеством ограничений (в отличие от рассмотренного выше метода оценки вклада в расчете на единицу ограничивающего фактора). Однако он применим только к двухпродуктовым моделям, так как каждому товару/услуге должна соответствовать одна координатная ось. [c.370]
Методы линейного программирования. Первые исследования по постановке и разработке методов решения линейных оптимизационных задач были проведены в тридцатые годы Л. В. Канторовичем. В 1939 г. им была опубликована книга Математические методы организации и планирования производства , в которой впервые был ш сдложен эффективный метод решения задач оптимизации для моделей с линейными ограничениями и линейным критерием. Однако достоинство книги состояло не только в этом — в пей было показано, что модели экономических систем широкого класса могут быть достаточно точно построены на основе использования линейных соотношении. В дальнейшем эти идеи получили широкое распространение, и в настоящее время липейиые модели и методы оптимизации в таких моделях составляют основу, на которой базируется исследование прикладных экономических задач. [c.50]
