Данный способ расчета наиболее обоснован теоретически и дает самые точные результаты в практическом применении. Но дело осложняется рядом обстоятельств. Во-первых, качество большинства видов продукции, а, следовательно, и его уровень формируются чаще не одним, а несколькими свойствами, причем значимость их в формировании полезности различна. Встает сложная проблема определения их значимости. Во-вторых, полезность продукта находится чаще в нелинейной зависимости от значения свойств (частных качественных характеристик), а это означает непостоянство их значимости. Указанные сложности преодолимы, но не всегда. [c.39]
Графическое изображение соотношения между экономией от повышения качества дизельного топлива и сопутствующими ему затратами приведено на рис. 4.1 в форме т.н. коробки качества - совмещенном графике, по ординате которого показаны одновременно дополнительные расходы по сероочистке и получаемая от этого экономия, а по абсциссе - содержание серы. Рис. 4.1 и табл. 4.1 подтверждают основные из упомянутых ранее закономерностей. Это -нелинейность зависимости экономии и затрат от значений качественных параметров, наличие предела насыщения, снижающаяся предельная полезность качества, повышающиеся предельные затраты на дополнительный прирост качества. Отсюда вывод не существует постоянных коэффициентов значимости качественных характеристик продукции. Они являются функциями оцениваемых свойств. Поэтому, строго говоря, все способы синтеза комплексного показателя качества продукции, основанные на применении фиксированных коэффициентов значимости единичных показателей по формулам (3.14), (3.15), (3.16) искажают действительность. Избежать этого можно, применяя прямой, экономически прозрачный показатель полезности продукта. В самом способе его расчета и в структуре его компонентов заключена возможность учета нелинейности и всех других особенностей реального соотношения эффекта повышения качества и затрат по его обеспечению. Полностью отвечает сложной природе качества такой расчет его уровня, при котором непосредственно соизмеряются полезность продукции и затраты на её изготовление и эксплуатацию. Такой показатель называется интегральным. [c.86]
Технико-экономические показатели вариантов формируются в процессе решения задачи на основе заданных закономерностей (например, нелинейная зависимость затрат от изменения масштабов производства). Эти закономерности определяются с помощью статистических методов, [c.165]
Выбор математической формы связи при моделировании себестоимости добычи нефти, как показывает практика, целесообразно проводить методом перебора известных уравнений регрессий с переходом от менее сложных форм к более сложным. Часто случается так, что одна часть факторов связана с себестоимостью добычи нефти линейной зависимостью, другая — нелинейной. Поэтому удобнее поиск искомой формы связи начинать с линейной зависимости, затем проверить нелинейную зависимость, а потом перейти к более сложным формам связи (приложение 1). При выборе формы связи необходимо стремиться к получению достаточно простой по решению и удобной для экономической интерпретации модели. Модель себестоимости добычи нефти должна также отвечать условиям адекватности при включении в нее возможно меньшего числа факторов. Последнее обстоятельство указывает на то, что оценка значимости факторов с последующим отсевом менее существенных из них не утрачивает своей актуальности и на этом этапе исследования. [c.18]
Хотя большинство видов издержек представляется линейной зависимостью, показанной ранее, существуют издержки, поведение которых имеет нелинейную зависимость. Один из вариантов изменения издержек, когда они возрастают на дискретную величину при конкретных объемах производства, не увеличиваясь при этом в промежутках между данными конкретными объемами, представлен на правой нижней диаграмме рис. 7.1. Иногда издержки такого типа называют поэтапно-постоянными . Примером издержек такого типа могут быть расходы на заработную плату инспекторам. [c.180]
| Рис. 44.1. Графическое представление нелинейной зависимости показателей |  |
| Рис. 10.4. Динамика затрат (нелинейная зависимость) |  |
Примеры нелинейных зависимостей достаточно обширны. Например, экономическая эффективность производства возрастает или убывает непропорционально изменению масштабов производства величина затрат на производство партии деталей возрастает в связи с увеличением размеров партии, но не пропорционально им. И в том, и в другом случае мы, по существу, сталкиваемся с проблемой переменных и условно-постоянных издержек.. [c.168]
Дальнейшее совершенствование постановки проблемы, сформулированной в [19], шло по пути более точного отражения отдельных подсистем отрасли, полного охвата их взаимозависимости и взаимовлияния, придания моделям такой математической формы, в которой они могли бы быть реализованы на ЭВМ. Так, в работе [20] уделено внимание формированию функционала задачи на основе учета нелинейной зависимости затрат от объема добычи района-поставщика, глубины и технологии переработки нефти и т. п. (в работе [19] рассматривалось также расширение исходной постановки за счет отказа от условий независимости затрат от объемов добычи и транспортировки нефти. В этом случае задача сводилась к модели квадратичным функционалом и решалась методом последовательных приближений). [c.198]
В качестве основы линеаризации можно использовать приближение нелинейных зависимостей некоторыми простыми функциями [92]. В данном случае наиболее подходящей формой аппроксимирующего полинома является ступенчатая функция (рис. 39, на котором качественно изображен график характерного нелинейного норматива и его аппроксимация). Остановимся несколько подробней на ступенчатой аппроксимации. Пусть функция Я (а) определена на отрезке [аЪ] и имеет вид, изображенный на рис. 43. [c.224]
В случае нелинейной зависимости линейный коэффициент корреляции теряет смысл, и для измерения тесноты связи применяют так называемое корреляционное отношение, известное также под названием индекс корреляции [c.323]
Определение нелинейной корреляционной зависимости. Одним из способов нахождения зависимости является метод замены переменной. Этот метод довольно часто используется при решении различных математических задач. Он заключается в том, что независимый фактор заменяется некоторой функцией этого фактора, которая переводит нелинейную зависимость в разряд линейных. [c.57]
Например, рассмотрим нелинейную зависимость вида у = х2. Это не что иное, как парабола с вершиной в начале координат. Зависимость явно нелинейная. Чтобы убедиться в этом, достаточно посмотреть на график этой зависимости (рис.2.3). [c.57]
Вид нелинейной зависимости Подстановка [c.58]
Линейная и нелинейная зависимость [c.98]
Как мы уже отметили в предыдущем разделе, график разброса может помочь в определении, имеется или нет зависимость между двумя наборами данных. Если зависимость существует, то она либо линейная, либо нелинейная. Линейная зависимость представлена прямыми линиями, а нелинейная зависимость — кривой. На последующих примерах мы покажем соотношения обоих типов. [c.102]
Эти данные представлены на рис. 3.4. И снова, похоже, график разброса показывает на существование зависимости между годом и объемом выручки. Точки, нанесенные на графике, больше соответствуют кривой, а не прямой линии, как это показано на графике. Такой тип нелинейной зависимости часто возникает при отображении данных экономического характера, где инфляционные процессы искажают исходные цифры. Возможно, если данные, представленные в нашем примере, сравнить в реальном выражении, без учета инфляции, то полученный в результате график представит линейную зависимость. Для подтверждения этого необходим дальнейший анализ фактических данных. [c.103]
Альтернативный подход к анализу нелинейной зависимости состоит в подгонке номинального выражения к имеющимся данным. Другими словами, переменные х и у могут быть соотнесены с помощью уравнения со степенями х. Общее уравнение можно записать в следующем виде [c.126]
В определенных обстоятельствах можно использовать коэффициент ранговой корреляции в качестве альтернативного показателя оценки зависимости между двумя наборами значений. Так, часто трудно получить точные показатели некоторых значений, и поэтому единственный надежный метод состоит в расстановке переменных по порядку, иначе говоря — в ранжировании значений. Коэффициент корреляции ранжированных значений называется коэффициентом ранговой корреляции, и он вычисляется по упрощенной формуле, которая приведена в этой главе. Значимая корреляция между двумя переменными подразумевает наличие линейной зависимости между ними. Методы регрессии можно использовать для определения уравнения наилучшей прямой линии, линии регрессии. Уравнение регрессии записывается в виде у = а + Ьх. Это уравнение можно использовать для оценки значения у при заданном значении х. Так, например, объем выручки от реализации можно рассчитать исходя из заданной суммы расходов на рекламу. Нелинейная зависимость между переменными должна быть преобразована в линейную, и только потом следует проводить базовый анализ регрессии. [c.128]
Линейная и нелинейная зависимость 102 Линейное программирование 260—307 Линейный график 19 Линия наилучшего соответствия 117 [c.419]
Так, в работе [9] учитывались нелинейная зависимость затрат от района-поставщика, глубины переработки, технологии и т. п. Модель представлялась в виде задачи квадратичного программирования, которая решалась методом последовательных приближений. [c.95]
Должна учитываться нелинейная зависимость экономических показателей от технологических, так как в противном случае значительная часть вариантов не рассматривается и полученные решения оптимальны на суженном множестве допустимых вариантов развития объектов. [c.97]
В силу нелинейной зависимости ряда использованных при вычислении коэффициентов целевой функции нормативов [16] функционал модели (31) оказывается также нелинейным. [c.114]
Если по какой-то причине присутствует нелинейная зависимость, то линейная функция Y = а + ЬХ не обеспечит хорошего согласия. [c.260]
Рассматривает линейную зависимость между зависимой и независимой переменными. Описывается в форме Y = а + ЬХ, в то время как нелинейная регрессия предполагает нелинейную зависимость, например, экспоненциальную и квадратическую функции. См. Регрессионный анализ. [c.462]
| Рис. 3.4. Графическое представление нелинейной зависимости показателей доходов и расходов при увеличении объемов производства | 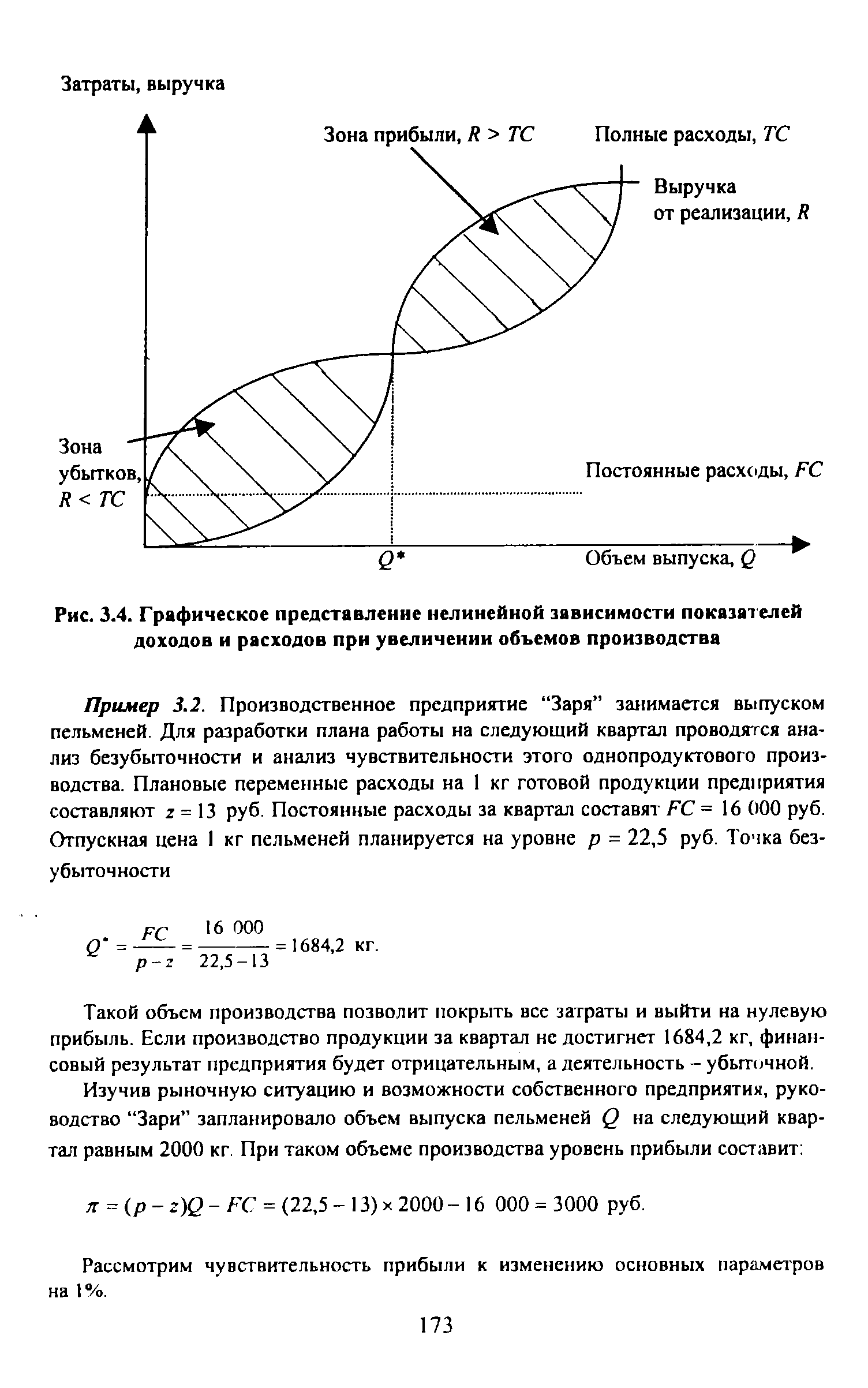 |
Нормальный спад . При высоких ценах сбывается принципиально меньше товаров, чем при низких. Это относится как к линейным, так и нелинейным зависимостям класса выпукло-вогнутых убывающих функций (в отношении результативного признака), как это показано на рис. 8.3. [c.150]
Множество переменных представляет собой объединение о>д и Ц. ифй. В него входят независимые и зависимые переменные. В данной постановке задачи в качестве независимых переменных (управляющих параметров) выбраны диаметр и рабочее давление в трубопроводе. При этом диаметр может принимать дискретные значения, обусловленные выпускаемым сортаментом труб, а рабочее давление - любое значение из области допустимых для данного диаметра. Переменные связаны между собой рядом зависимостей. К ним относятся функциональные линейные и. нелинейные зависимости между скоростью движения пульпы в трубопроводе, его производительностью и диаметром потерями напора в трубопроводе, его диаметром и протяженностью, скоростью движения и характеристиками пульпы и т.д. записываются они в виде равенств и неравенств. [c.64]
Более явно нелинейная зависимость выражена в формуле, предложенной польским исследователем А. Томашевским для определения степени соответствия любого из свойств из- [c.71]
Объект нашего исследования — качество — объект чрезвычайно сложный. Комплексная оценка — не произвольное соединение оценок отдельных свойств. Вероятно, вполне правомерно рассматривать качество как систему. Если принять, что система — множество взаимосвязанных элементов, выступающих как единое целое, то, очевидно, качество продукции— типичный пример системы. А если это так, то можно ли считать, например, что среднеарифметическая (или другие средние) адекватно отражают реальные связи между свойствами Представляется, что нет. Средняя арифметическая (как и другие средние) предполагает отсутствие корреляции между отдельными свойствами или такую малую корреляцию, что ею можно пренебречь. Однако на самом деле многие свойства (если не большинство) взаимосвязаны. Разумеется, из этого не следует вывод о нежелательности применения средних величин. Ненужно представлять, что модели, основанные на использовании средних, как и модели, основанные на линейной и нелинейной зависимости между показателем и оценкой (о которых мы говорили в предыдущем параграфе), являются достаточно грубыми и не снимают необходимости в разработке более точных и достоверных моделей. [c.89]
Таким образом, основной недостаток при использовании в решении экстремальных экономических задач в непрерывной постановке заключается в отсутствии в большинстве случаев методов их решения. Кроме того, во многих случаях неизвестными являются даже и сами виды экономических зависимостей, делающие задачи нелинейными (зависимость затрат на перевозку единицы продукции от объема перевозок, зависимость затрат труда от объема производства, себестоимости единицы продукции от объема производства и т. п.). [c.122]
Теперь обратимся к случаю нелинейной зависимости функции полезности F от качественного параметра Kf. ПриК ,= 1 F0=l+0,5 l°-5=l,5. [c.50]
Теснота связи между переменными величинами может иметь различные значения, если рассматривать ее с позиции характера зависимости (линейная, нелинейная). Если установлена слабая связь между переменными в линейной зависимости, то это совсем не означает, что такая связь должна быть в нелинейной зависимости. Показателем, хаРактеРизУющим значимость факторов при различной форме связи, яв/1яется корреляционное отношение. Оценка факторов по корреляционному отношению уже на этом этапе анализа позволяет предварительно уст0новить вид многофакторной связи, что служит хорошей предпосылкой ПРИ выборе конкретной модели исследуемого показателя. [c.17]
Однако большинство затрат не находится в линейной зависимости от производственной мощности. Переменные затраты с линейной зависимостью легко анализировать, прогнозировать при планировании и контроле затрат. Нелинейные затраты трудно планировать, но их также необходимо учитывать при принятии управленческих решений. Метод линейной апроксимации позволяет превратить переменные затраты с нелинейными зависимостями в линейные. Этот метод использует понятие релевантных уровней. [c.55]
Подчеркнем, что не следует абсолютизировать выводы, к которым можно прийти, анализируя график. Во-первых, приведенное графическое представление взаимосвязи выручки и расходов от объема выпуска продукции основано на весьма условном предположении об их прямо пропорциональной зависимости. Во-вторых, не следует полагать, что область доходов безгранично велика — при определенном насыщении рынка зависимость между показателями меняется. Фактически это выражается в том, что излишне произведенная продукция не находит сбыта по ранее установленной цене. Сформулированные условности в теоретическом смысле элиминируются, если перейти от линейных зависимостей к нели-нейным, однако на практике установление аналитического представления нелинейной зависимости затруднено. [c.420]
Для1 нахождения лучшей подстановки можно использовать визуальный метод, когда на глаз определяется вид нелинейной зависимости, связывающей результирующий параметр и независимый фактор, а можно выбор наилучшей замены осуществлять, используя коэффициент корреляции. Та подстановка, у которой коэффициент корреляции является максимальным, и является наилучшей. [c.58]
Нелинейная зависимость. Проанализировав формулу (35), Э. Роосе [172] пришел к выводу о необходимости введения в нее дополнительного параметра — показателя брака Р /бр> за который принимается нижнее допустимое значение показателя. [c.71]
Однако это не значит, что формулами, описывающими. линейную и нелинейную зависимости, нельзя пользоваться. В настоящее время в большинстве отечественных методик для оценки свойств используются линейные зависимости, а во многих зарубежных — нелинейные. Но нужно иметь в виду, что несмотря на большое количество методик, необходимость в разработке более точных и достоверных моделей остается актуальной задачей. В этом отношении стоит обратить внимание на следующее обстоятельство ни в одной из известных в литературе отечественных и зарубежных методик оценки качества при вычислении относительных показателей Kif тех свойств, оценка которых должна производиться в зависимости от воздействия этих свойств на органы чувств человека, так называемых органолептических свойств, не учитывается основное положение экспериментальной психологии — психофизиологический закон Вебера — Фехнера, в соответствии с которым связь между абсолютным [c.73]
Смотреть страницы где упоминается термин Нелинейная зависимость
: [c.212] [c.68] [c.98] [c.98] [c.123] [c.420] [c.43]Смотреть главы в:
Количественные методы анализа хозяйственной деятельности -> Нелинейная зависимость
