Как видно из табл.3.7. наибольшая теснота характерна для параболической второго порядка формы связи, корреляционные отношения у которой превышают критические (составляющие при уровне значимости, равном 0,05, для линейной и гиперболической форм связей от 0,392 до 0,588, для параболической второго порядка - 0,424 - 0,606) / 5 /. [c.99]
В корреляционно-регрессионном анализе мерой тесноты и надежности служат корреляционные отношения, абсолютные значения которых лежат в границах от нуля до единицы. Причем чем ближе эти значения к единице, тем надежнее и теснее исследуемая взаимосвязь. [c.105]
Проведенные расчеты показали, что для анализируемой установки АВТ-6 корреляционные отношения составили [c.105]
Корреляционные отношения изменения себестоимости единицы целевой продукции и производительности технологических установок (для различных форм связи) [c.108]
Зависимость (19) интерпретируется в линейном или нелинейном виде. Ее оптимизируют по остаточной дисперсии, критерию Фишера, коэффициентам корреляции или корреляционному отношению и по сходимости прогнозных значений с фактическими. [c.42]
После выполнения указанных выше действий необходимо приступить к многофакторному анализу себестоимости добычи нефти с применением корреляционных методов. Основная задача анализа на этом этапе заключается в нахождении связи между исследуемым показателем и отобранными факторами, а также между отдельными факторами и в оценке тесноты установленной связи. Эта задача решается с помощью парных и частных коэффициентов корреляции и корреляционного отношения. Методы [c.16]
Расчетные значения эксплуатационных затрат на извлечение жидкости хорошо согласуются с эмпирическими (ё = 5,7 %), множественное корреляционное отношение высокое (т = 0,98) и существенное (t-— 154,4 по сравнению с табличным 2,58). [c.35]
Что касается измерения тесноты связи при криволинейной форме зависимости, то здесь используется не линейный коэффициент корреляции, а корреляционное отношение, формула которого имеет следующий вид [c.69]
Из экономике-математических методов в анализе наиболее распространен корреляционно-регрессионный анализ. Он используется для определения тесноты зависимости между показателями, которые не связаны между собой функционально. Теснота связи между показателями измеряется коэффициентом корреляции для прямолинейной зависимости и корреляционным отношением для криволинейной зависимости. [c.81]
Статистический анализ показывает, что уравнение значимо Рф = 5,054 при /"табл = 3,01, корреляционное отношение равно 0,9959, ее"стандартная ошибка равна 0,0015. Среднее квадратическое отклонение расчетной себестоимости от фактической равно 0,018. Средняя ошибка аппроксимации 1,1%. [c.90]
Корреляционное отношение и его ошибки......... [c.95]
Корреляционное отношение п его ошибки......... [c.98]
Метод корреляционного и регрессионного анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости. Теснота связи между изучаемыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости исчисляется коэффициент корреляции. [c.158]
Расчет исходных данных для определения корреляционного отношения при криволинейных зависимостях [c.137]
Подставив полученные значения в формулу (7.8), определим величину корреляционного отношения [c.137]
В случае нелинейной зависимости линейный коэффициент корреляции теряет смысл, и для измерения тесноты связи применяют так называемое корреляционное отношение, известное также под названием индекс корреляции [c.323]
Параметры корреляционного уравнения, а также корреляционное отношение и коэффициент корреляции определяются обычно из выборки, следовательно, полученные показатели не являются точными оценками. [c.324]
Такой же способ применяется для оценки значимости корреляционного отношения. [c.324]
По аналитической группировке можно измерить связь с помощью еще одного показателя эмпирического корреляционного отношения. Этот показатель обозначается греческой буквой г (эта). Он основан на правиле разложения дисперсии, согласно которому общая дисперсия s2y равна сумме внутригрупповой и межгрупповой дисперсий. [c.128]
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Соответственно оно рассчитывается как отношение факторной дисперсии к общей дисперсии результативного признака [c.129]
Можно рассчитать и показатель множественной тесноты связи -совокупное эмпирическое корреляционное отношение. [c.131]
Чтобы понять, насколько целесообразно в том или ином случае применение районированного отбора, можно воспользоваться корреляционным отношением т]. Согласно правилу сложения дисперсий средняя из внутригрупповых дисперсий может быть представлена как [c.179]
Корреляционное отношение используется и при корректировке величины [c.179]
Для измерения тесноты связи применяется несколько показателей. При парной связи теснота связи измеряется прежде всего корреляционным отношением, которое обозначается греческой буквой г). Квадрат корреляционного отношения - это отношение межгрупповой дисперсии результативного признака, которая выражает влияние различий группировочного факторного признака на среднюю величину результативного признака, к общей дисперсии результативного признака, выражающей влияние на него всех причин и условий. Квадрат корреляционного отношения называется коэффициентом детерминации [c.232]
Формула (8.1) применяется при расчете показателя тесноты связи по аналитической группировке (см. гл. 6). При вычислении корреляционного отношения по уравнению связи (уравнению парной или множественной регрессии) применяется формула (8.2) [c.233]
Если уравнение выбрано неверно или сделана ошибка при расчете его параметров, то сумма квадратов в числителе может оказаться большей, чем в знаменателе, и отношение утратит тот смысл, который оно должно иметь, а именно какова доля общей вариации результативного признака, объясняемая на основе выбранного уравнения связи его с факторным признаком (признаками). Чтобы избежать ошибочного результата, лучше вычислять корреляционное отношение по другой формуле (8.3), не столь наглядно выявляющей сущность показателя, но зато полностью гарантирующей от возможного искажения [c.233]
В числителе формулы (8.3) стоит сумма квадратов отклонений фактических значений признака у от его индивидуальных расчетных значений, т. ё. доля вариации этого признака, не объясняемая за счет входящих в уравнение связи признаков-факторов. Эта сумма не может стать равной нулю, если связь не является функциональной. При неверной формуле уравнения связи или ошибке в расчетах возрастают расхождения фактических и расчетных значений, и корреляционное отношение снижается, как логически и должно быть. [c.234]
Теснота парной линейной корреляционной связи, как и любой другой показатель, может быть измерена корреляционным отношением ц. Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи - коэффициент корреляции г . Этот показатель представляет собой стандартизованный коэффициент регрессии, т. е. коэффициент, выраженный не в абсолютных единицах измерения признаков, а в долях среднего квадратического отклонения результативного признака [c.241]
Это выражение соответствует выражению т)2 (см. формулу (8.2)). Тождество коэффициента детерминации и квадрата корреляционного отношения служит основанием для интерпретации величины г2л, как доли общей дисперсии результативного признака у, которая объясняется вариацией признака-фактора х (и связью между вариацией обоих признаков). Собственно говоря, основным показателем тесноты связи и следовало бы считать коэффициент детерминации [c.242]
Эта сумма квадратов - общая вариация объема прибыли - равна 222,4. Теперь можем построить меры тесноты связи теоретическое корреляционное отношение [c.255]
Оба квадрата корреляционных отношений соответствуют по содержанию ранее рассмотренному коэффициенту детерминации (8.1) и (8.2) и интерпретируются как показатели доли вариации результативного признака, объясняемой за счет вариации группировочно-го, факторного признака (и, конечно, связанных с ним прочих факторов). В данном примере связь является тесной. Различие в том, что в эмпирическом корреляционном отношении связь признаков не абстрагирована от случайных влияний прочих факторов на вариацию у, не связанных с вариацией х. [c.255]
Решая эту систему, получаем значения параметров a, b и с. Показателем тесноты параболической корреляции является корреляционное отношение, вычисляемое как корень квадратный из выражения (8.2). [c.264]
Для измерения тесноты параболической корреляционной связи находим вариацию результативного признака у, объясняемую вариацией фактора j как сумму квадратов отклонений расчетных величин у от средней величины у, взвешенных на число предприятий. Общая сумма квадратов отклонений всех 136 значений у, от средней величины составляет 4624,7. Таким образом согласно формуле (8.1), корреляционное отношение [c.266]
Корреляционное отношение для данной связи, рассчитанное по формуле (8.1) [c.268]
Теснота связи между явлениями измеряется корреляционным отношением. Количественная оценка тесноты связи в зависимости от корреляционного отношения приведена в табл. 2.6. [c.49]
| Таблица 2.6. Качественная оценка тесноты связи при различных значениях корреляционного отношения | 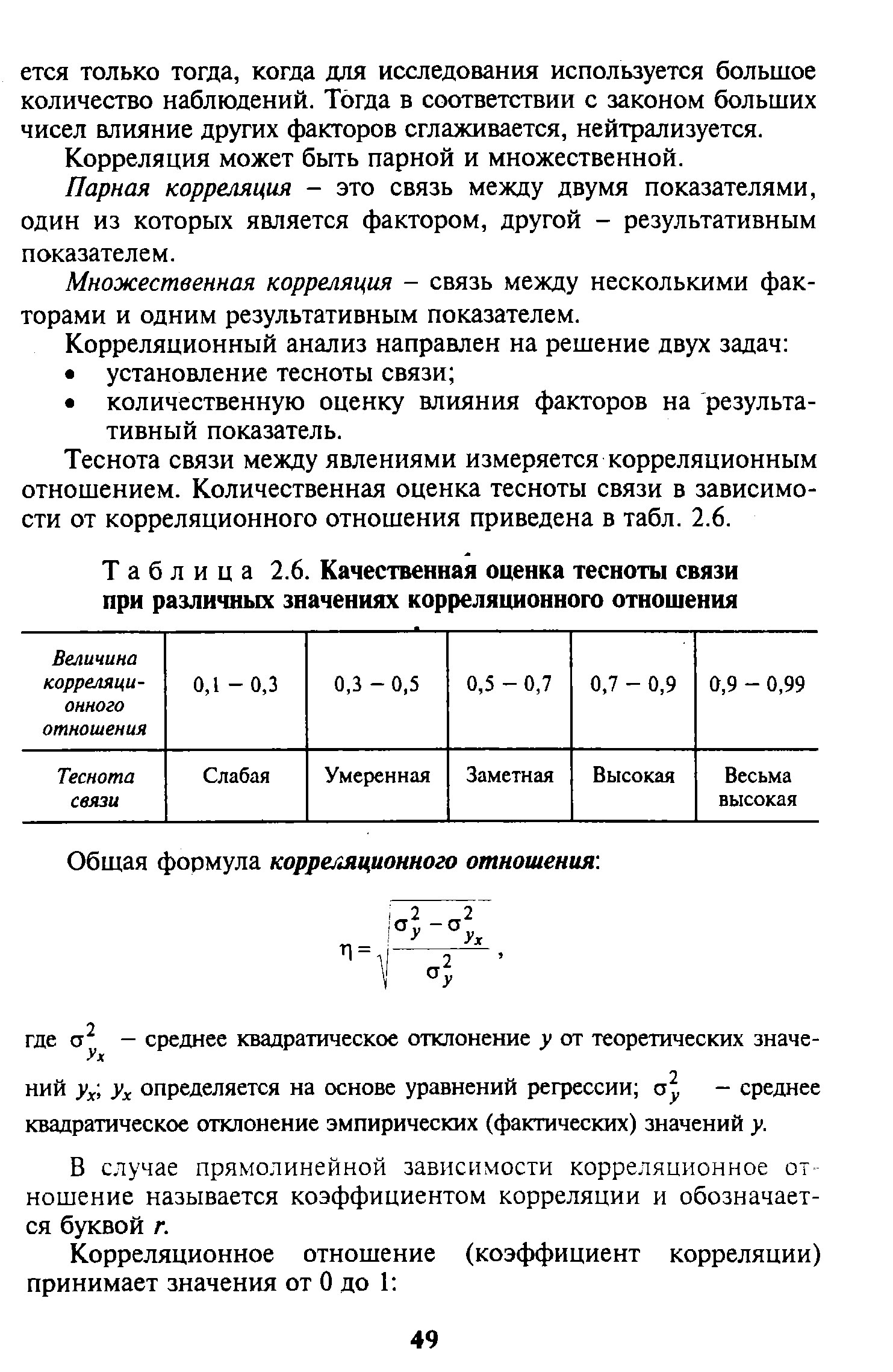 |
Общая формула корреляционного отношения [c.49]
Корреляционное отношение (коэффициент корреляции) принимает значения от 0 до 1 [c.49]
Если связь криволинейная, то прежде всего определяются теоретические значения ух. С этой целью решается уравнение регрессии, описывающее связь между изучаемыми показателями. Затем рассчитывается корреляционное отношение. [c.50]
Корреляционные отношения изменения энергетических расходов и суточной производительности установки АВТ-6 АО УНПЗ (для различных форм связи) [c.99]
Теснота связи между переменными величинами может иметь различные значения, если рассматривать ее с позиции характера зависимости (линейная, нелинейная). Если установлена слабая связь между переменными в линейной зависимости, то это совсем не означает, что такая связь должна быть в нелинейной зависимости. Показателем, хаРактеРизУющим значимость факторов при различной форме связи, яв/1яется корреляционное отношение. Оценка факторов по корреляционному отношению уже на этом этапе анализа позволяет предварительно уст0новить вид многофакторной связи, что служит хорошей предпосылкой ПРИ выборе конкретной модели исследуемого показателя. [c.17]
Значения частных коэффициентов корреляции и других критериев оценки существенности факторов представлены в табл. 5, в которой приняты следующие обозначения г. — частный коэффициент корреляции t. — критерий, характеризующей надежность п. — корреляционное отношение t. — критерий, характеризующий надежность -К. — коэффициент, характеризующий криволинейность связи (линейная, нелинейная). [c.28]
Статистический анализ уравнения показал следующее фактическое значение F-критерия равно 57,77 при табличном значении 3,33-(для 5%-ного уровня значимости), корреляционное отношение равно 0,99747. Проверка по -критерию показала, что корреляционное отношение значимо (tk — 42,484 при табл = 2,228). Коэффициент множественной детерминации, равный 0,9949, показывает, что вариация себестоимости, объясняемая вариацией изучаемых факторов, составляет 99,49%. [c.89]
Тогда F = 28,5. Критическое значение F-критерия из табл. 3 приложения F(a = 005 (//., = 2 2 =, 7) = 3,59. Таким образом Рфакт > крш,, следовательно, HQ отклоняется. Действительно, скорость оборота средств является очень важным фактором формирования прибыли, на это указывало и значение эмпирического корреляционного отношения г) = 0,881. [c.214]
Смотреть страницы где упоминается термин Корреляционное отношение
: [c.129] [c.179] [c.243] [c.255]Прикладная статистика Исследование зависимостей (1985) -- [ c.73 , c.98 , c.133 ]
Математические методы моделирования экономических систем Изд2 (2006) -- [ c.147 ]
