Корреляционный анализ используется для выявления наличия и оценки тесноты связи между качественными и количественными факторами. [c.42]
Оценка тесноты связи по коэффициенту корреляции проводится по следующей схеме [c.323]
При моделировании и оценке тесноты связи приходится учитывать тот факт, что анализ ведется на основе динамических рядов. Об относительно высокой автокорреляции временных рядов валютного курса сказано выше. [c.670]
Обычно считают связь сильной, если г > 0,7 средней тесноты, при 0,5 <, г < 0,7 слабой при г < 0,5. Не следует, особенно работая с ЭВМ, гнаться за большим числом знаков коэффициента корреляции. Во-первых, исходная информация редко имеет более трех значащих точных цифр, во-вторых, оценка тесноты связи не требует более двух значащих цифр. [c.242]
Теснота связи между явлениями измеряется корреляционным отношением. Количественная оценка тесноты связи в зависимости от корреляционного отношения приведена в табл. 2.6. [c.49]
| Таблица 2.6. Качественная оценка тесноты связи при различных значениях корреляционного отношения | 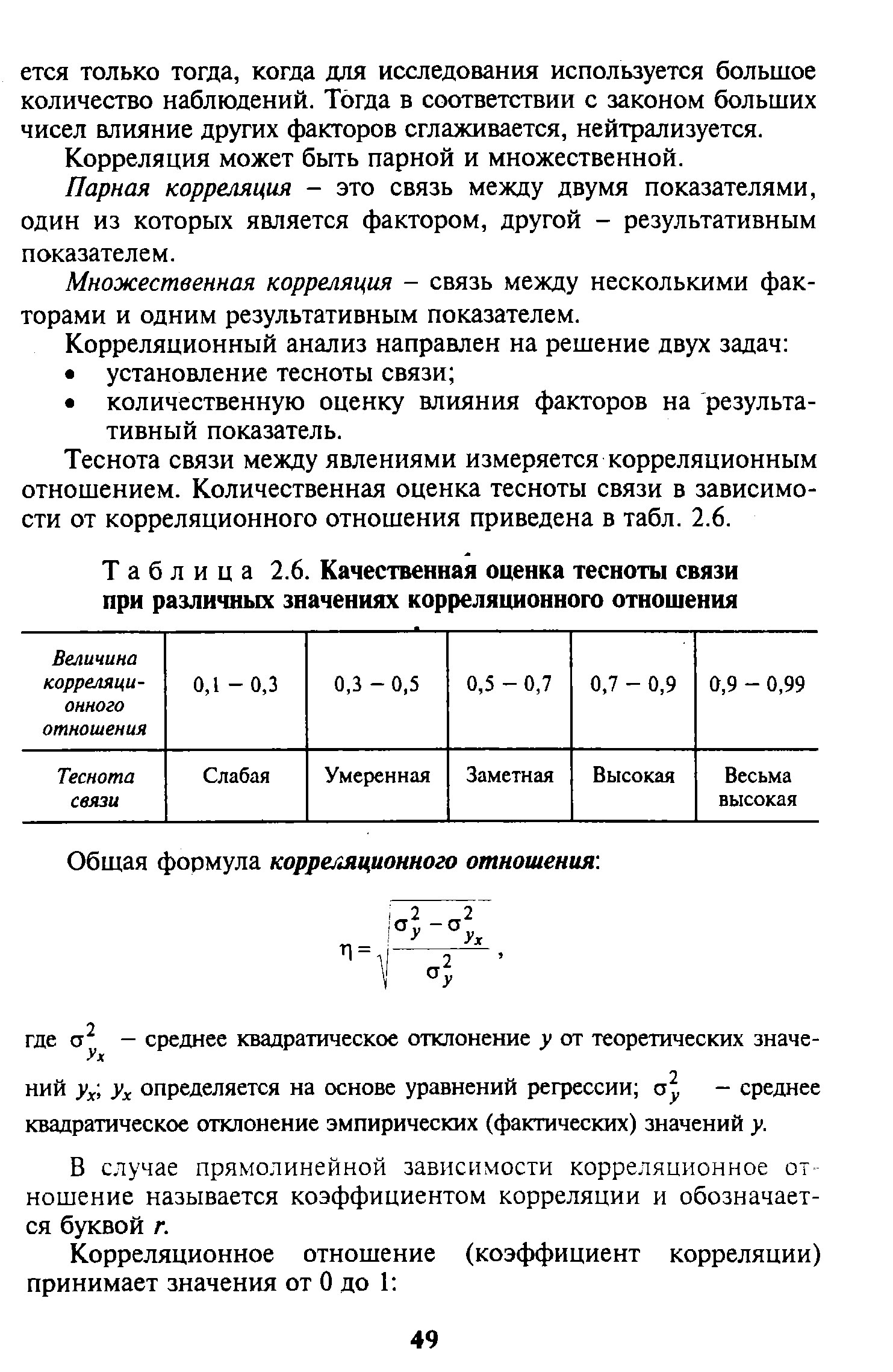 |
По степени тесноты связи различают следующие количественные критерии оценки тесноты связи. [c.110]
Количественные критерии оценки тесноты связи [c.110]
Измерение тесноты и направления связи является важной задачей изучения и количественного измерения взаимосвязи социально-экономических явлений. Оценка тесноты связи между признаками предполагает определение меры зависимости вариации результативного признака от одного (при изучении парных зависимостей) или нескольких (множественных) факторных признаков. [c.122]
Выше, в 3.3, для оценки тесноты связи между переменными был введен выборочный коэффициент линейной корреляции. Если переменные коррелируют друг с другом, то на значении коэффициента корреляции частично сказывается влияние других переменных. В связи с этим часто возникает необходимость исследовать частную корреляцию между переменными при исключении (элиминировании) влияния одной или нескольких переменных. [c.128]
Процесс регрессионного анализа экономических явлений состоит из следующих этапов 1) предварительная обработка статистических данных и выбор факторов-аргументов 2) оценка тесноты связи между признаками и выявление форм связи 3) разработка многофакторной модели изучаемого явления и ее анализ 4) использование результатов анализа для совершенствования планирования и управления данным явлением. [c.173]
Оценку тесноты связи между признаками производим при помощи парных коэффициентов корреляции, определяемых по формуле (6). [c.177]
Для количественной оценки тесноты связи между отобранными показателями определяем коэффициенты парной корреляции (табл. 15). [c.177]
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи рху = 0,3944 (по сравнению с [c.16]
Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи [c.73]
R 2х х = 0,9407 определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и потому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 90%) детерминированность результата в модели факторами х и хг. [c.76]
Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадет с индексом корреляции Ryx = ryv где z — преобразованная величина [c.81]
Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции. Так, для степенной функции yx = a-xb после перехода к логарифмически линейному уравнению lny=lna + b-lnx может быть найден линейный коэффициент корреляции не для фактических значений переменных хпу,а для их логарифмов, т. е. rln)inx. Соответственно квадрат его значения будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для у, а для его логарифмов [c.83]
Тогда независимо от того, что фактор х задан линейно, а факторы х2, хг, х4 — в логарифмах, оценка тесноты связи может быть произведена с помощью линейного коэффициента множественной корреляции. Так, если рассматриваемая модель в стандартизованном виде оказалась следующей [c.117]
При установлении тесноты связи между 7 и Jf решается задача установления строгости соблюдения функциональной зависимости между изменениями 7 и X. Для оценки тесноты связи между случайными переменными величинами используются показатели [c.76]
| Таблица 4 Качественная оценка тесноты связи | 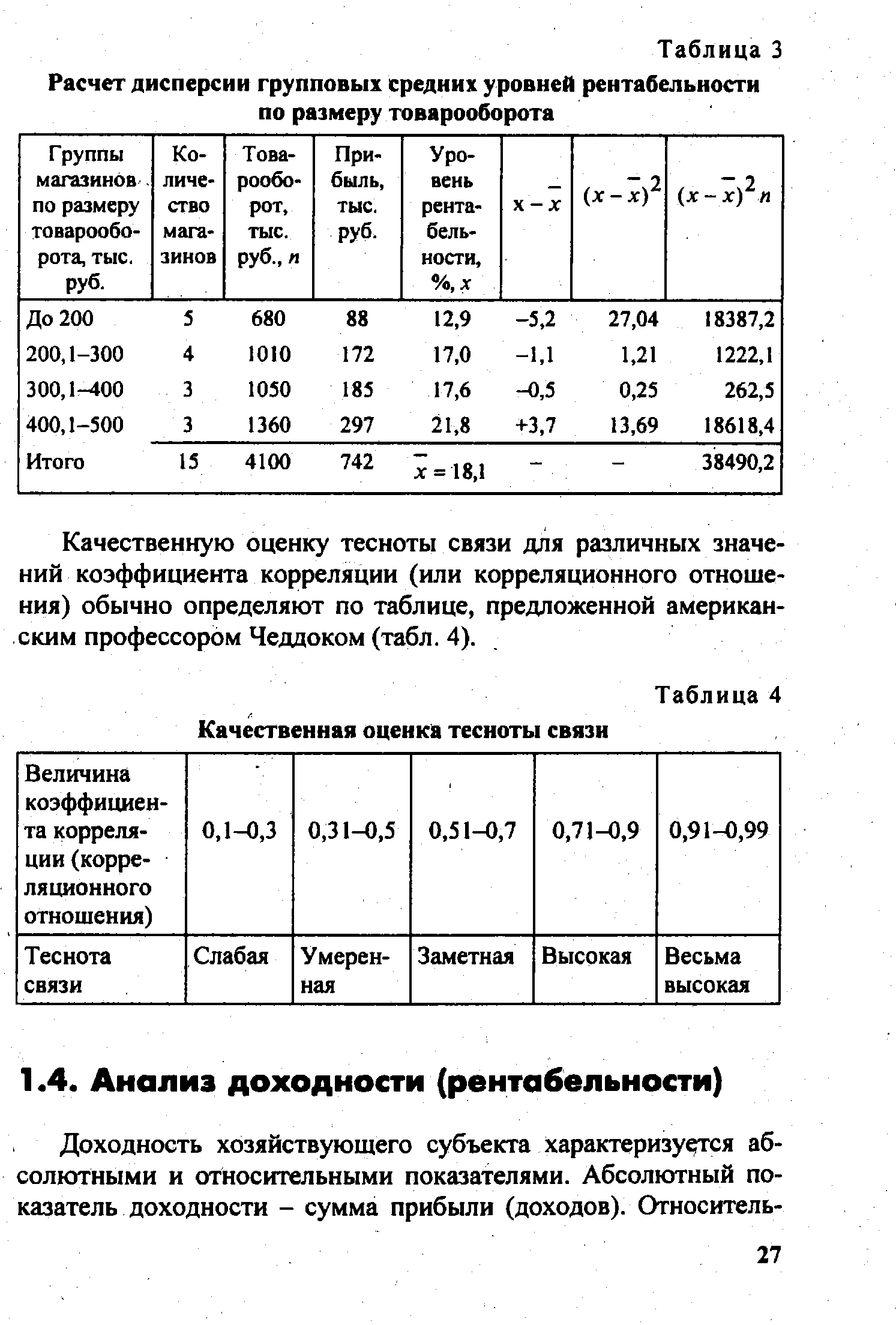 |
| Таблица 2.5 Показатель оценки тесноты связи спроса с факторами по коэффициенту корреляции | 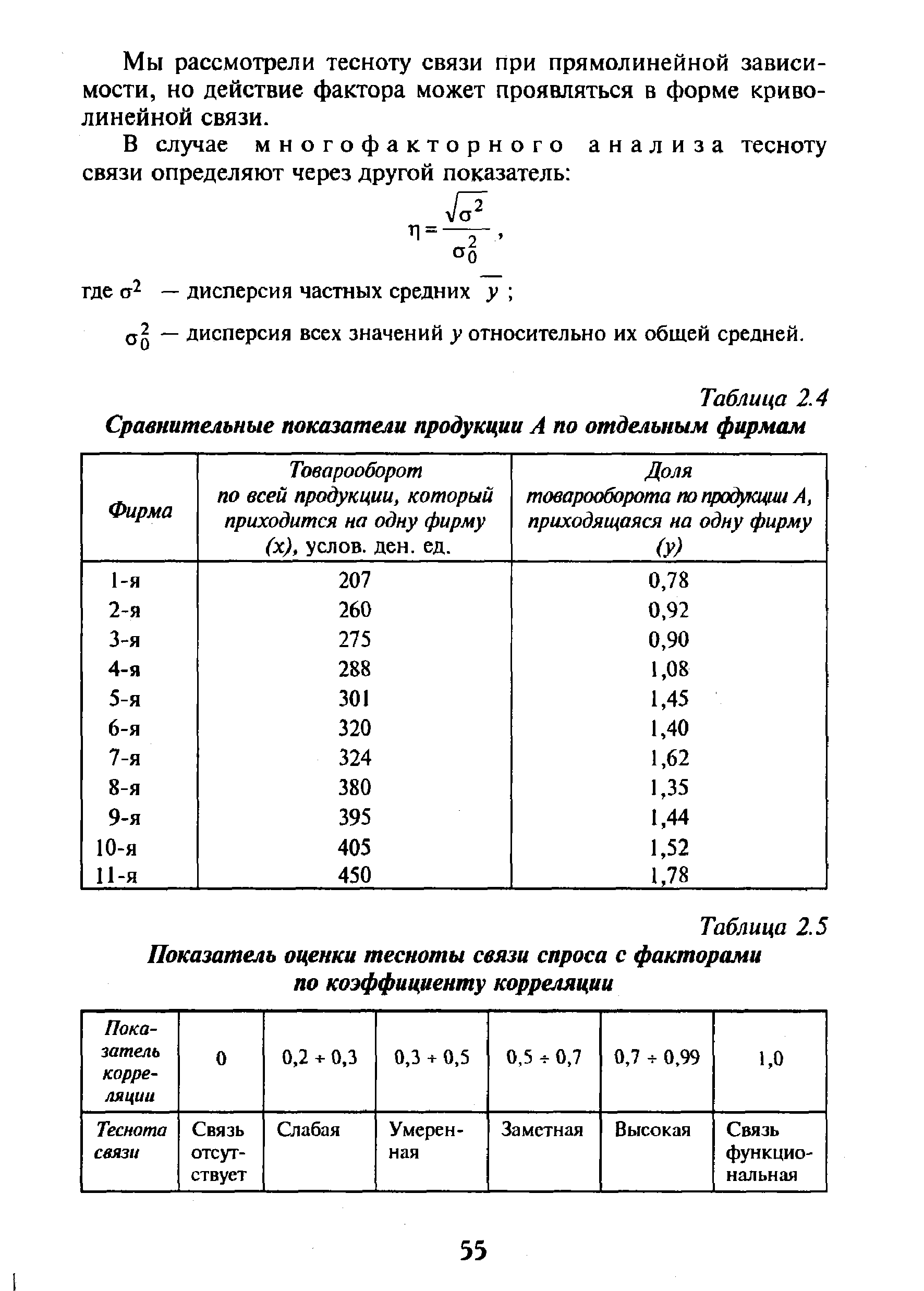 |
Для оценки тесноты связи факторов используется [c.355]
Для оценки тесноты связи между мерой труда и поощрением важное значение имеет анализ соотношения темпов роста производительности труда и средней заработной платы. Это соотношение рекомендуется рассчитывать как отношение темпов прироста средней заработной платы и товарной продукции на одного работника промышленно-производственного персонала. [c.73]
Для проверки гипотезы о наличии связи между себестоимостью железнодорожных перевозок у в каждой группе хозяйств и каждым предварительно выбранным фактором х и оценки тесноты связи между ними определялись парные коэффициенты корреляции гух, если связь линейная и корреляционное отношение Г УХ, если связь нелинейна (гиперболическая). [c.116]
Среди выборочных корреляционных методов (например, при оценке тесноты связи ранжированных данных экспертов) широко используется ранговая корреляция. Она применяется только тогда, когда есть возможность определить последовательность рангов (порядковых номеров), а не измерить только пары величин двух переменных. [c.250]
Корреляционное отношение используется для оценки тесноты связи между двумя явлениями, в частности для определения тесноты связи исходного ряда у( с теоретическим рядом у . Корреляционное отношение определяют по данным, сгруппированным по объясняющей переменной по следующей формуле [c.148]
Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы — параметрические — и принято называть корреляционными. [c.131]
По существу, и корреляционная таблица, и корреляционное поле, и эмпирическая линия регрессии предварительно уже характеризуют взаимосвязь, когда выбраны факторный и результативный признаки и требуется сформулировать предположения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов. [c.132]
Практически для количественной оценки тесноты связи широко используют линейный коэффициент корреляции. Иногда его называют просто коэффициентом корреляции. Если заданы значения переменных X и У, то он вычисляется по формуле [c.132]
Рассмотрим вопрос о регрессии. В ряде случаев именно от его решения — оценки уравнений регрессии — зависят оценки тесноты связи, а они, в свою очередь, дополняют результаты регрессионного анализа. Прежде всего следует определить перечень независимых переменных X, включаемых в уравнение. Это должно делаться на основе теоретических положений. Список X может быть достаточно широк и ограничен только исходной информацией. На практике теоретические положения о сути взаимосвязи подкрепляются парными коэффициентами корреляции между зависимой и независимыми переменными. Отбор наиболее значимых из них можно провести с помощью ЭВМ, выбирая в соответствии с коэффициентами корреляции и другими критериями факторы, наиболее тесно связанные с У. Параллельно решается вопрос о форме уравнения. Современные средства вычислительной техники позволяют за относительно короткое время рассчитать достаточно много вариантов уравнений. В ЭВМ вводятся значения зависимой переменной У и матрица независимых переменных X, принимается форма уравнения, например линейная. Ставится задача включить в уравнение k наиболее значимых X. В результате получим уравнение регрессии с k наиболее значимыми факторами. Аналогично можно выбрать наилучшую форму связи. Этот традиционный прием, называемый пошаговой регрессией, если он не противоречит качественным посылкам, достигает приемлемых результатов. Первоначально обычно берется линейная модель множественной регрессии [c.134]
Оценки тесноты связи (корреляции) могут играть двоякую роль. Это — самостоятельные характеристики, дающие представление и о взаимодействии изучаемых факторов, и об аппроксимации фактических данных аналитической функцией. Поэтому расчет показателей множественной корреляции предполагает оценку уравнений регрессии. [c.137]
Такие оценки носят общий характер и не претендуют на статистическую строгость, поскольку не дают гарантий на вероятностную достоверность. Поэтому в статистике принято использовать более надежные критерии для оценки тесноты связи, основываясь на рассчитанных значениях коэффициента парной корреляции (КПК). [c.17]
Коэффициент корреляции гху используется для оценки тесноты связи между показателями X и 7 [c.70]
Оценка тесноты связи между переменными по коэффициенту парной корреляции не решает всех вопросов. В частности,этот показатель не учитывает частной ("чистой") корреляции между изучаемь М явлением и характеризующими его факторами. Известно, что кФкУи аяся хорошая теснота связи между двумя показателями может возникнуть под влиянием третьего показателя, который имеет высокую теС"отУ связи с общими исследуемыми показателями. Чтобы исключить нежелательное влияние этих показателей и более достоверно установить зНачимость каждого фактора с учетом одновременного действия других, в0°Дят частный коэффициент корреляции разных степеней. Проверка надежности этого коэффициента по одному из известных критериев [21, 4Ь 46, 48] позволяет более точно оценить значимость каждого фактора, выбранного для модели. Необходимо оценить существенность факторов в зависимости от характера связи между ними, а также между отдельными факторами и исследуемым показателем. [c.17]
Ранговый коэффициент корреляции р может быть использован и для оценки тесноты связи между обычными количественными переменными. Достоинство р здесь заключается в том, что нахождение этого коэффициента не требует нормального распределения переменных, линейной связи между ними. Однако необходимо учитывать, что при переходе от первоначальных значений переменных к их рангам происходит определенная потеря информации. Чем теснее связь, чем меньше корреляционная зависимость между переменными отличается от линейной, тем ближе коэффициент корреляции Спирмена р к коэффициенту парной корреляции г. [c.80]
Качественную оценку тесноты связи для различных значений коэффициента корреляции (или корреляционного отношения) обычно определяют по таблице, предложенной американским профессором Чеддоком (табл. 4). [c.27]
Выбрав форму уравнения регрессии, начинаем отбор факторов для ее построения. Отбор факторов осуществляется в 2 этапа I) качественный экономический анализ всех учитываемых факгоров 2) непосредственное включение факторных признаков в уравнение регрессии на основе количественной оценки тесноты связи данных факторов с результативным показателем. Эти два этапа органически связаны между собой и с другими этапами моделирования в целом. [c.77]
Коэффициент контингенции всегда меньше коэффициента ассоциации. Сравнение этих коэффициентов, исчисленных по одним и тем же данным, свидетельствует о том, что коэффициент контингенции дает более осторожную оценку тесноты связи. Заметим также, что Кк = К. [c.144]
Зная коэффициент корреляции, можно дать качественно-количественную оценку тесноты связи. Используются, например, специальные табличные соотношения (так называемая шкала Чеддока). [c.16]
Фи-коэффициент применяют только к таблице 2 х 2, а коэффициент сопряженности признаков С oeffi ient) используют для оценки тесноты связи в таблицах любого размера. [c.577]
