Многочлены более высокой степени, дающие меньшую остаточную дисперсию и наиболее близко проходящие от экспериментальных значений удельных расходов, дают при экстраполяции значительный выброс прогнозируемой величины. Это еще раз подтверждает то, что экономические явления, как правило, хорошо описываются полиномами низких степеней. [c.23]
Зависимость (19) интерпретируется в линейном или нелинейном виде. Ее оптимизируют по остаточной дисперсии, критерию Фишера, коэффициентам корреляции или корреляционному отношению и по сходимости прогнозных значений с фактическими. [c.42]
Оператор 85. Подпрограмма вычисления остаточной дисперсии уравнения регрессии, построенного в операторе 84. Алгоритм подпрограммы представлен на рис. 9. [c.75]
Операторы 112—119. Формирование матриц парных коэф- фициентов корреляции для построения уравнения регрессии (оператор 116, см. рис. 8) и вычисления остаточной дисперсии ( оператор 117, см. рис. 9) раздельно для данных по каждому типу буровых установок. [c.75]
| Рис. 9. Алгоритм вычисления остаточной дисперсии многофакторной регрессионной модели / | 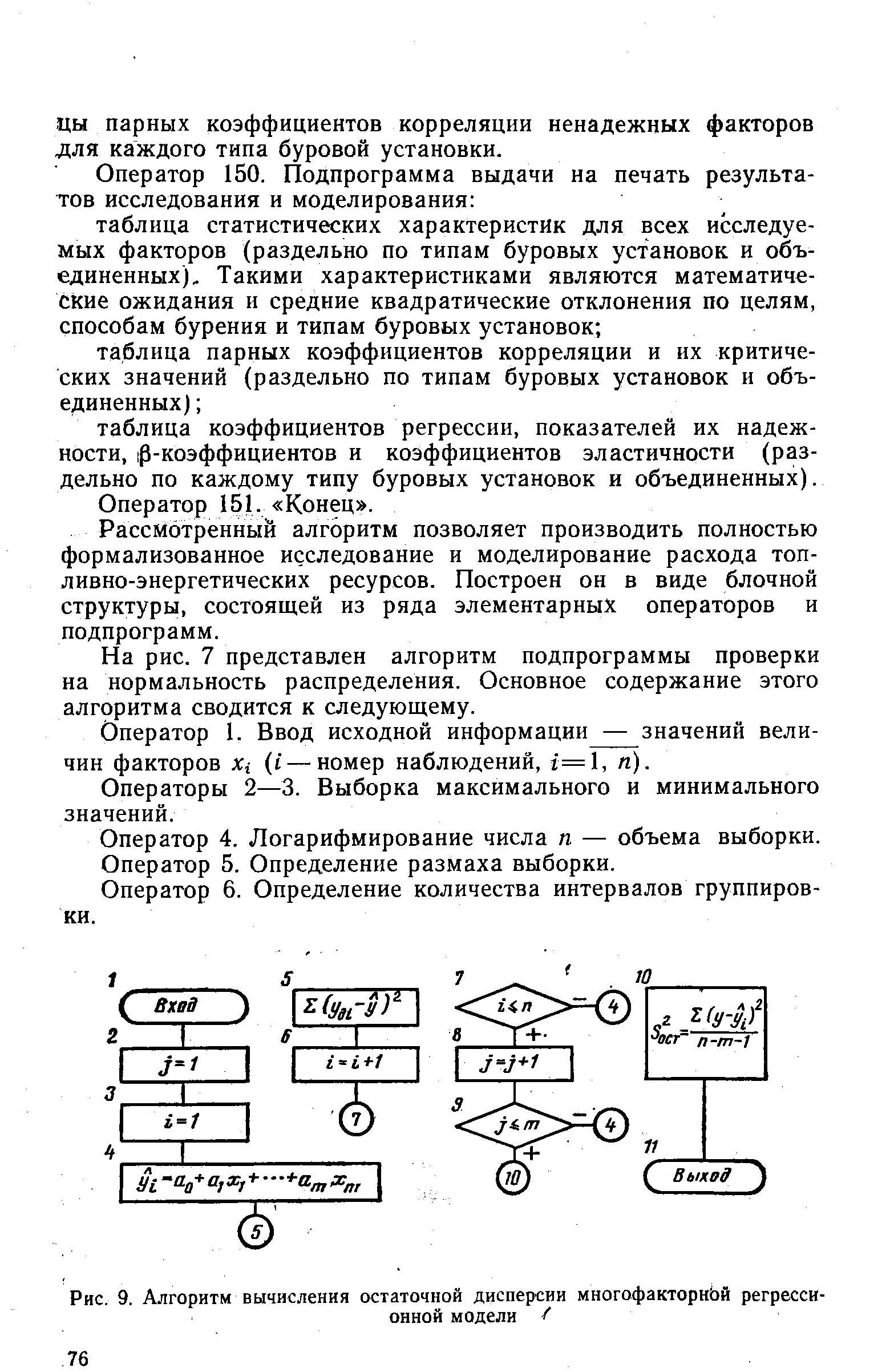 |
Оператор 10. Расчет величины остаточной дисперсии многофакторной регрессионной модели. [c.78]
Продолжительность периода исследования при пользовании этим методом обусловлена главным образом целями и задачами конкретного экономического анализа. При построении экономико-статистических моделей для анализа себестоимости добычи нефти по статьям и отдельным элементам затрат период анализа фактического состояния должен позволять исключить изменение влияния факторов во времени. В данном случае необходимо учитывать то обстоятельство, что в статических моделях остаточная дисперсия тем выше, чем продолжительнее анализируемый период. [c.15]
Последняя модель себестоимости добычи нефти, как показывает оценка ее по известным критериям, удовлетворяет условиям адекватности. Коэффициент множественной корреляции R составляет 0,98, что свидетельствует о том, что колеблемость исследуемого показателя более чем на 96 % определяется факторами, включенными в эту модель. При оценке по f-критерию (t R = 30,5) можно утверждать, что с вероятностью 0,99 факторы, включенные в модель, имеют существенную связь с исследуемым показателем (t a n = 2,58). Средняя ошибка аппроксимации составляет всего лишь 2,9 %, а F-критерий, характеризующий уровень остаточной дисперсии, превышает критическое (табличное) значение в четыре раза. К этому следует добавить, что полученная модель себестоимости добычи нефти представляет собой достаточно простую форму связи, легко решается и поддается экономической интерпретации. [c.30]
Формула временного тренда отыскивается посредством перебора ряда форм связи (по критерию остаточной дисперсии). Наиболее часто употребляемые формы связи приведены в работах [18, 22, 33, 47 и др.]. (Формы связи, использованные при выполнении данной работы, приведены в приложении ) [c.54]
Остаточная дисперсия вычисляется по формуле [c.287]
Построение соответствующих моделей факторов и сравнение остаточных дисперсий позволили отобрать наиболее рациональные виды зависимостей 1. [c.102]
Оу — дисперсия по линии регрессии °ост остаточная дисперсия. [c.76]
Чем плотнее фактические значения yt располагаются относительно линии регрессии, тем меньше остаточная дисперсия (больше факторная дисперсия) и, следовательно, больше величина гу. [c.328]
Таким образом, коэффициент множественной корреляции, как и величина остаточной дисперсии, характеризует качество подбора уравнения регрессии. [c.328]
Числитель подкоренного выражения есть остаточная дисперсия результативного признака. [c.248]
Модели разрабатывались в отдельности по каждому критерию эффективности К], >2,. .., Y-J. Каждая из полученных моделей оценивалась по степени ее адекватности (определенности) фактическим данным путем расчета коэффициента регрессии (множественной) R (достаточность выборочной совокупности и ее однородность по выбранным признакам позволили получить очень высокие значения / от 0,82 до 0,99) дисперсионных отношений FI и FI и остаточной дисперсии е (во всех случаях значения F, FI и е отвечали табуляции с вероятностью полученных результатов Р — 0,95). [c.223]
Q остаточная дисперсия результативного признака от воздействия всех факторов, кроме выделенного, — aj [c.468]
Равенство (4.20) означает, что несмещенная оценка s2 параметра ст2 или выборочная остаточная дисперсия s2 определяется по формуле [c.97]
По отклонениям от тренда была исчислена остаточная дисперсия, а затем среднеквадратическое отклонение эмпирических данных от тренда. Для того чтобы стандартизовать эту величину, было исчислено ее процентное отношение к среднему уровню ряда (коэффициент аппроксимации). Он составил почти 26%. Это означает, что рынок развивался неустойчиво, в своем развитии цены колебались в значительной степени. [c.160]
Точность модели оценивается величиной относительной остаточной дисперсии (чем меньше, тем точнее модель). Взаимосвязь прогнозируемого параметра g с совокупностью учитываемых факторов оценивается коэффициентом множественной корреляции между расчетным и фактическим значениями, по значению которого и решается вопрос на предмет практического использования модели (0,7 — минимальное значение). [c.124]
Используя эти модели, можно количественно описать исследуемый процесс в статическом состоянии от фактора времени. Интерпретация каждой функции в отдельности с точки зрения адекватности ее анализируемому процессу облегчается при помощи статистических оценок. В качестве последних принимается остаточная дисперсия и доля случайной вариации в общей вариации, называемая F-критерием. Абсолютная величина этих оценок для выбранной функции должна быть минимальной в сравнении с этими же оценками для других функций. Такой подход обусловлен необходимостью выявить наименьшее влияние случайных величин на изучаемую тенденцию. Чем меньше случайные колебания, а следовательно и о ст, тем адекватнее функция. [c.41]
Далее строится новая модель без исключенного фактора, рассчитывается для этой модели остаточная дисперсия, которая [c.193]
Остаточная дисперсия модели V шага оказалась выше, чем модели IV шага. Следовательно, влияние исключенного на последнем шаге фактора хг (техническая фондовооруженность) на выработку продукции является значимым. [c.195]
В качестве оптимального по программе п POL I" выбирается многочлен с наименьшей остаточной дисперсией. На печать выдаются следующие данные начальная степень полинома, конечная степень полинома, число заданных наблюдений, исходные данные с указанием реального масштаба времени, остаточная дисперсия для заданных степеней полиномов, коэффициенты оптимального полинома, значения величины х с указанием соответствующих ей значений величины , приближение по оптимальному полиному в каждой из заданных точек, абсолютная ошибка приближения, относительная ошибка приближения, экстраполяция прогнозируемой величины в необходимые моменты времени. Многочисленные расчеты, проведенные на ЭВМ ЕС-1022 для большого числа материалов, нормируемых в бурении и добыче, показали, что наиболее удачными в смысле достоверности прогнозирова- ния, являются полиномы 1-й, 2-й и реже 3-й степеней. [c.23]
Изменение себестоимости добычи нефти и попутного газа во времени носит, в целом, криволинейный характер, хотя и неявно выраженный. Функции выбирают путем построения степенного и показательного уравнений регрессии —"с последующим сравнением сумм квадратов отклонений расчетных значений себестоимости добычи нефти и попутного газа от фактических (табл. 18). Из табл. 18 видно, что наименьшую остаточную дисперсию по НГДУ Укрнефти имеет кинетическая производственная функция. [c.69]
Воздействие неучтенных случайных факторов и ошибок наблюдений в модели (3.22) определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии а2. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия1. [c.62]
В множественной корреляции, когда на результативный признак влияет несколько факторных признаков, показатель тесноты связи, индекс корреляции (Rvvl v2 vn) строится по аналогичной формуле. Только в остаточной дисперсии отражено влияние всех факторов [c.202]
Подставляя значения логарифма факторного признака, заполняем гр. 8 таблицы (равенство ее итога с итогом гр. 3 свидетельствует о точности расчета). После этого производится последовательный расчет гр. 9 (разность гр.З и гр. 8 возводится в квадрат). Итог гр. 9 делится на число групп в таблице, в результате получена остаточная дисперсия о2ост = 1,55488. Общая дисперсия результативного признака определяется по формуле (средняя квадрата результативного признака минус квадрат его средней) [c.206]
Рассчитанные данные позволяют определить правильность выбора функции для построения модели. Рассчитывается среднеквад-ратическое отклонение эмпирических данных от теоретической линии как корень квадратный из остаточной дисперсии. В нашем примере оно составляет 1,247. Исчислив его процентное отношение к среднему значению результативного признака, получим коэффициент аппроксимации [c.206]
Критерием для выбора наиболее адекватного вида функции служит абсолютная минимальная величина остаточной дисперсии
Блок 17 — перебор функций и выбор тех из них, которым соответствует наименьшее абсолютное значение остаточной дисперсии о"ост. Дополнительным требованием к TO T является отношение остаточной дисперсии к квадрату средней арифметической, т. е. ao T/F3<0,02. Из заданного набора выбирается не более шести видов функции. [c.173]
Группа вспомогательных модулей дает возможность рассчитать обобщающие статистические характеристики. К последним можно отнести средние значения (у, х) общую и остаточную дисперсию-(о2, OO T) коэффициент вариации (У) коэффициенты парной (гух) и множественной корреляции (R). Последовательность вычислений этих величин проводится по известным в статистике формулам и при их исчислении затруднений не возникает. Поэтому рассматривать в данной статье эти алгоритмы модулей не представляется необходимым. Для краткости ниже приводится шифр модулей и формул, расчет которых он обеспечивает. [c.38]
Из таблицы видно, что на I шаге наименьшее значение -критерия соответствовало коэффициенту при xw (уровень заводской предметной специализации). В связи с этим была построена новая модель без фактора xw. Остаточная дисперсия модели II шага (5остг = 1221,1) меньше остаточной дисперсии модели первого шага (5ост, = 1228,5), в результате чего влияние фактора х1№ на выработку товарной продукции признается незначимым. Отсюда знак соответствующего коэффициента регрессии axlt) неустойчив. Этим можно объяснить тот, казалось бы, противоречащий эконо-194 [c.194]
Наименьший -критерий в модели II шага соответствует коэффициенту фактора х15 (удельный вес числа рабочих вспомогательных цехов). Остаточная дисперсия модели III шага, построенной без фактора х1Ъ, оказалась ниже остаточной дисперсии модели II шага, что говорит о незначимости влияния х15 на выработку продукции. [c.195]
