Число предприятий (цехов, участков) п по которым обобщаются данные, должно быть достаточно представительным. Его определяют по формуле выборочной совокупности [c.164]
В качестве информационной основы группировки служит или генеральная совокупность однотипных объектов, или же выборочная совокупность. В первом случае используются преимущественно материалы общегосударственных или региональных переписей во втором — типологическая выборка. [c.51]
Поскольку конъюнктура конкретного товарного рынка характеризуется как общеэкономическими, так и специфическими, только ей присущими факторами, то центральной проблемой создания методики анализа и прогнозирования спроса является разработка нетоварных моделей, в ходе которой предстоит учитывать множество переменных величин, а также факторов, не поддающихся количественному измерению. Наиболее эффективным в выявлении этих факторов является метод проведения обследования или анкетирования на базе выборочной совокупности. [c.326]
Например, пусть существует совокупность счетов, 5% которых оформлены с ошибками. Если взять случайную выборку в составе 50 счетов, то в ней может быть обнаружено разное число счетов с ошибками. Их может не быть вовсе, но может быть 6, 7 и более. Вероятность каждого возможного числа отклонений в выборке образует выборочное распределение. Выборочное распределение для описанной выборочной совокупности показано в табл. 5.3. Из приведенных в таблице данных видно, что при выборке в 50 единиц из совокупности с нормой отклонений в 5% вероятность получения выборки с отклонениями составит 1 — 0,0769 = 0,9231, или 92,31%. Вероятность появления в выборке не больше двух отклонений составит 54,05%. [c.51]
Та совокупность, из которой производится отбор, называется генеральной совокупностью отобранные данные составляют выборочную совокупность. Эти данные представляют интерес постольку, поскольку дают основание для суждений о параметрах и свойствах генеральной совокупности. [c.158]
Объем генеральной совокупности обозначают N, объем выборочной совокупности - k. [c.159]
Выборочная совокупность формируется по принципу массовых вероятностных процессов без каких бы то ни было исключений от принятой схемы отбора необходимо обеспечить относительную однородность выборочной совокупности или ее разделение на однородные группы единиц. При формировании выборочной совокупности должно быть дано четкое определение единицы отбора. Желателен приблизительно одинаковый размер единиц отбора, причем результаты будут тем точнее, чем меньше единица отбора. [c.160]
Как указывалось в п. 7.2, при проведении выборочного наблюдения используются различные способы формирования выборочной совокупности случайный отбор - повторный или бесповторный, механический, серийный, типический. Вид выборки влияет на величину ошибки выборки. При бесповторном отборе формула средней ошибки выборки дополняется множителем [c.171]
За рубежом практикуется проведение крупными фирмами панельных обследований потребителей. Панель - это постоянно действующая выборочная совокупность семей, добровольно и регулярно за плату предоставляющих маркетинговую информацию по разработанной фирмой программе. [c.226]
Панель - постоянно действующая выборочная совокупность семей, добровольно и регулярно за плату предоставляющая маркетинговую информацию по разработанной фирмой программе (п. 7.2). [c.238]
В процессе экономического анализа деятельности предприятия кроме интегральных показателей для менеджеров и экономистов важно определить взаимосвязи между отдельными параметрами производства. Поэтому экономический анализ подразделяется на комплексный, когда в выборочную совокупность параметров (показателей) входит множество факторов (например, в экономическую категорию себестоимость входят все виды затрат, связанных с производством и реализацией продукции), и факторный, когда анализируются изменения под влиянием отдельного фактора (например, себестоимость можно подразделить на затраты по отдельным факторам (затраты на материалы, расходы по заработной плате, расходы на содержание основных фондов, расходы по управлению) и проанализировать изменение процесса под влиянием каждого из этих факторов (рис. 1.3) [8] [c.20]
Модели разрабатывались в отдельности по каждому критерию эффективности К], >2,. .., Y-J. Каждая из полученных моделей оценивалась по степени ее адекватности (определенности) фактическим данным путем расчета коэффициента регрессии (множественной) R (достаточность выборочной совокупности и ее однородность по выбранным признакам позволили получить очень высокие значения / от 0,82 до 0,99) дисперсионных отношений FI и FI и остаточной дисперсии е (во всех случаях значения F, FI и е отвечали табуляции с вероятностью полученных результатов Р — 0,95). [c.223]
Анализ завершим сравнением фактически достигнутых и оптимальных значений степени использования ПМ предприятий по выборочной совокупности (табл. 4.34). [c.231]
Во всех случаях результаты выборочной совокупности должны быть распространены на совокупность генеральную. [c.186]
Определение совокупности. Так называемая генеральная совокупность включает в себя всех индивидуумов, которые, вероятно, могли бы быть охвачены в ходе проведения исследования. Очертить конкретную (выборочную) совокупность не всегда просто, как это кажется на первый взгляд. Возьмем, к примеру, анализ условий труда и вознаграждения работников. Какая совокупность рассматривается в данном случае Вполне возможно, [c.11]
Численность выборочной совокупности зависит от природы (характера) исследуемого социально-экономического явления. В выборочной совокупности должны быть представлены все типы единиц, имеющиеся в исследуемой совокупности. В противном случае выборочная совокупность не будет точно воспроизводить пропорции и зависимости, характерные для совокупности во всем ее объеме. [c.21]
Необходимо наличие достаточно большого объема исследуемой выборочной совокупности. [c.114]
В статистической практике общепринятыми являются следующие обозначения характеристик генеральной и выборочной совокупностей (таблица 12.1). [c.130]
| Таблица 12.1 Характеристики генеральной и выборочной совокупностей | 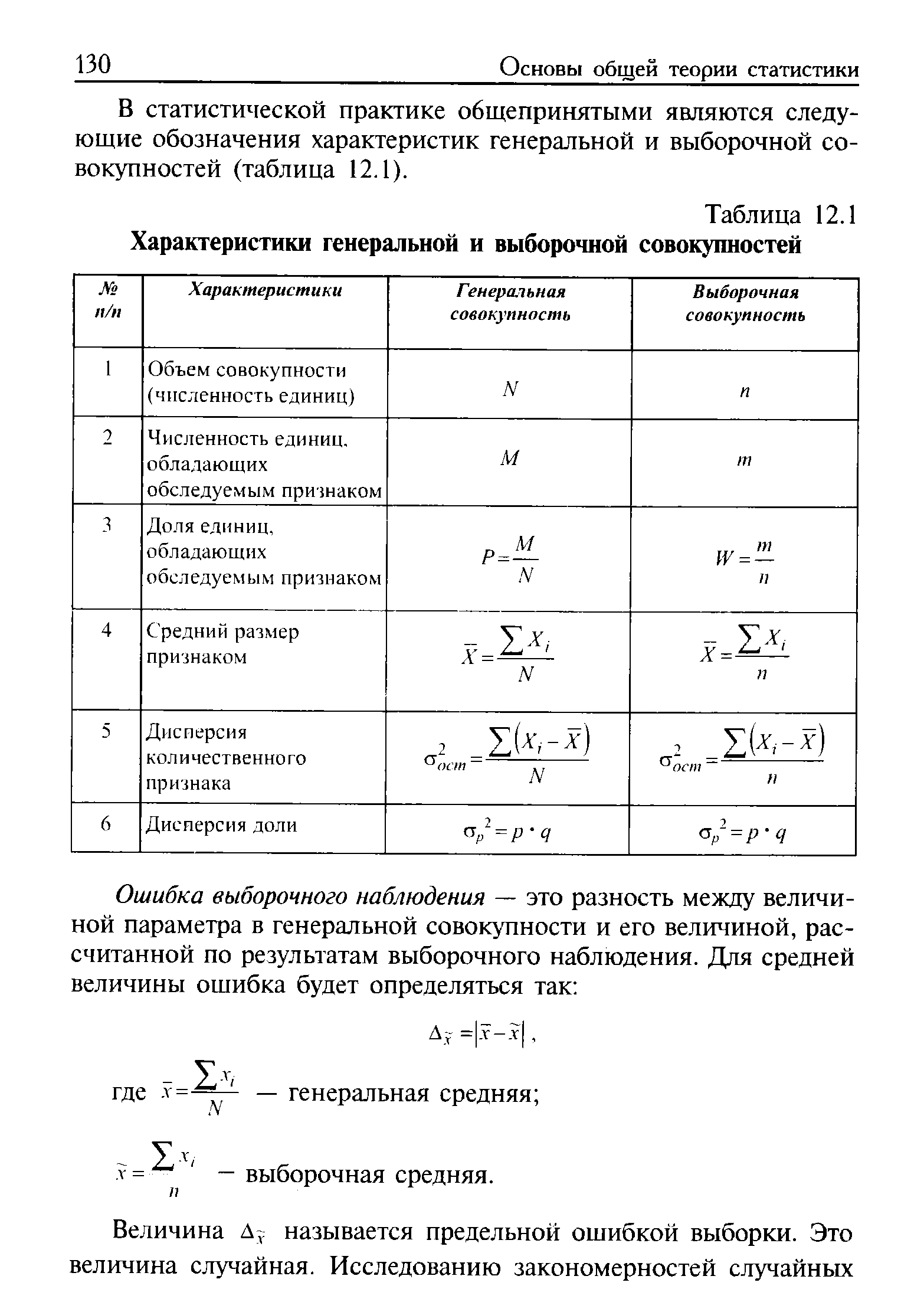 |
Соотношение между дисперсиями генеральной и выборочной совокупностей выражается формулой [c.132]
Следовательно, средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью. На величину вероятности указывает множитель /. [c.132]
Теорема Бернулли утверждает, что при достаточно большом объеме выборки вероятность расхождения между долей признака в выборочной совокупности (w) и долей признака в генеральной совокупности (р) будет стремиться к нулю. [c.133]
Из теоремы Бернулли следует, что величина расхождения между долей признака в выборочной совокупности (частостью) и долей этого признака в генеральной совокупности зависит, так же как и в расхождениях средних, от средней ошибки выборки. [c.133]
Однако доля признака в выборочной совокупности нам не известна, и мы вынуждены заменить ее через долю того же признака в генеральной совокупности, т.е. принять w = p, а дисперсию альтернативного признака принять за w(l — w). Тогда средняя ошибка выборки выразится формулой [c.134]
Выборочное наблюдение может быть осуществлено разными способами в зависимости от вида и метода отбора единиц совокупности. По виду различают индивидуальный, групповой и комбинированный отборы. При индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности, при групповом отборе — группы единиц, а комбинированный отбор предполагает сочетание группового и индивидуального отборов. [c.134]
Необходимое количество НГДУ выборочной совокупности п можно определить по формуле [32] [c.66]
Следовательно, выборочная совокупность в 76 НГДУ вполне достаточна для анализа. [c.66]
Корреляционный и регрессионный анализ был проведен по всей выборочной совокупности НГДУ, а также отдельно по НГДУ с растущей, стабильной и падающей добычей. Основные результаты реализации программы приведены в табл. 37. [c.83]
Уровень колеблемости показателей по НГДУ определяют с помощью среднеквадратичного отклонения, дисперсии и коэффициента вариации. Так, степень колеблемости уровня производительности труда по выборочной совокупности НГДУ по отношению к среднему показателю можно оценить с помощью среднеквадратичного отклонения в абсолютных единицах а и коэффициента вариации V в процентах по формулам [c.86]
Несмотря на кажущуюся надежность уравнения регрессии для всей выборочной совокупности НГДУ, использовать его для практических целей нельзя, так как проверка на нормальность распределения у показала, что р=1,043 значительно больше табличного значения, что свидетельствует о ненормальном распределении у. Поэтому необходимо рассмотреть вопрос о правомерности использования данной совокупности НГДУ для корреляционного и регрессионного анализа. Для этого проведено попарное сравнение дисперсий о2 отдельных групп НГДУ. [c.88]
Полученные для выборочной совокупности НГДУ уравнения регрессии (20) — (22) могут точно не совпадать с истинной зависимостью, характерной для генеральной совокупности НГДУ. Поэтому необходимо найти доверительный интервал Д, в котором с определенной вероятностью будет находиться расчетная величина производительности труда. Для среднего значения производительности труда у величину доверительного интервала при заданной доверительной вероятности, являющейся минимальной, рассчитывают по формуле [c.89]
Зная величину Эу для каждого фактора, можно оценить возможный рост (падение) производительности труда за счет изменения отдельных факторов. Так, если нам известно, что изменение дебита скважин на 1 % приводит к изменению производительности труда на k %, то, зная величину изменения указанного фактора в планируемом периоде, можно рассчитать ожидаемый уровень производительности труда. Так как уравнения регрессии (20) — (22) выражают зависимость производительности труда от основных факторов не по каждому НГДУ, а в среднем по выборочной совокупности их, то прогнозируемые значения производительности труда целесообразно рассчитывать по формулам (20) — (22) лишь в отраслевом масштабе для отдельных групп НГДУ с растущей, стабильной или падающей добычей. [c.145]
Для анализа выявляются факторы, влияющие на физический и моральный износ строительных машин. При производстве СМР эти факторы установлены с учетом выборочной совокупности по фуппам башенных кранов это фузоподъемность, организационно-технологические схемы монтажа, режим работы, возрастной состав, территориальный признак. Для примера проанализируем использование кранового оборудования при монтаже многоэтажных промышленных зданий. [c.238]
