X — среднеарифметическая величина экспертной оценки. Руководителем рабочей группы должна быть заранее установлена доверительная вероятность получения среднеарифметической выборочной экспертной оценки с относительной погрешностью не более С. Она обозначается буквой а. Обычно С принимается на уровне 0,1 V определяется по результатам пробного опроса экспертов, а доверительная вероятность невыхода С за установленные пределы а = 0,95 -ь 0.99. [c.59]
Изготовитель, не имеющий другой информации об истинном значении состава, кроме единичного результата испытаний, может считать, что продукт соответствует стандарту или техническим условиям с 95%-ной доверительной вероятностью, если результат /X/ соответствует [c.13]
Потребитель, не имеющий информации об истинном значении состава или свойства, кроме единичного результата испытании, должен считать, что продукт с 95 0-ной доверительной вероятностью не соответствует стандарту или техническим условиям, т.е. бракуется, если этот единичный результат /X/ удовлетворяет условию [c.14]
В качестве характеристики погрешности аттестованного значения СО принята полуширина интервала Ад, в котором с заданной доверительной вероятностью находится истинное значение величины, воспроизводимой СО в течение срока его действия. Характеристика погрешности исходных материалов выражается в виде полуширины интервала Дм, значение которого определяется по известным характеристикам погрешности определения содержания компонентов, подлежащих аттестации в материале СО и в исходных материалах. [c.22]
Характеристика погрешности градуировки (для 95%-ной доверительной вероятности), соответствующая измеряемому [c.48]
В зависимости от доверительной вероятности (68,3—99,7%) границы доверительных интервалов принимаются [c.135]
Задача формулируется следующим образом. Требуется найти оценку тг математического ожидания z величины Y (прогнозируемого уровня себестоимости) и построить доверительный интервал, соответствующий доверительной вероятности 0,99. [c.106]
Система телемеханики обеспечивает защитный отказ от исполнения ложной команды ТУ при выходе из строя любого элемента аппаратуры. Среднее время наработки на отказ каждого КП системы телемеханики должно быть не менее 8000 ч, аппаратуры ПУ — 2500 ч с доверительной вероятностью 0,8. [c.217]
Jn-l V40 -1 Если расчетное значение t выше табличного, то можно сделать заключение о том, что величина коэффициента корреляции является значимой. Табличные значения t находят по таблице значений критериев Стьюдента. При этом учитываются количество степеней свободы (V = п — 1)и уровень доверительной вероятности (в экономических расчетах обычно 0,05 или 0,01). В нашем примере количество степеней свободы равно п - 1 = = 40 - 1 = 39. При уровне доверительной вероятности Р = 0,05 t = 2,02. Поскольку /-фактическое (табл. 7.8) во всех случаях выше f-табличного, связь между результативным и факторными показателями является надежной, а величина коэффициентов корреляции — значимой. [c.148]
Доверительный интервал, доверительная вероятность и риск. Если случайная величина имеет нормальное распределение, то вероятность того, что ее значение появится в интервале (zo) около среднего значения зависит только от величины z, равной отношению отклонения Д от среднего значения и среднеквадратического отклонения z = Л/о. Интервал +Д называют доверительным интервалом, а соответствующую ему вероятность Р(г) — доверительной вероятностью, она равна при нормальном распределении функции Лапласа. Риск выхода за этот интервал R(z) = [1 — [c.59]
Коэффициент / зависит от размера выборки и доверительной вероятности, его значения приведены в табл. 6.2. При больших выборках распределение Стьюдента не отличается от нормального и [c.61]
| Таблица 6.2 Коэффициенты fy доверительной вероятности Стьюдента | 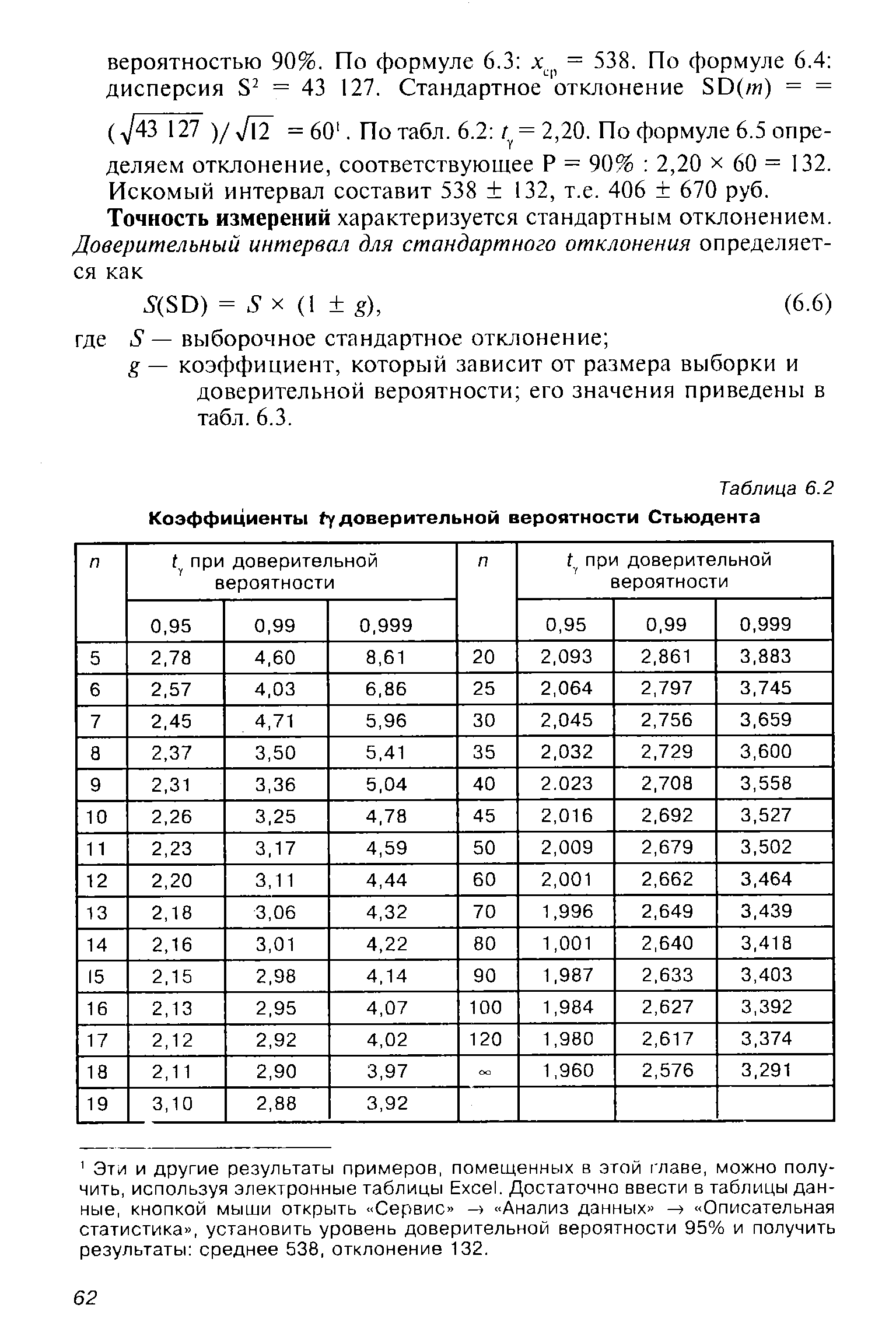 |
При одной норме величины ошибки риски зависят только от доверительной вероятности и определяются так [c.66]
Если допустить погрешность 10%, то размер выборки можно значительно сократить, до 3025 человек. Если 10% из них, т.е. 302— 303 человека, выберут рассматриваемую модель, то с доверительной вероятностью 90% общая минимальная доля покупателей модели составит (10 - 10 х 10/100) = 9%, максимальная — (10 + 10 х х 10/100) = 11%. [c.67]
Чтобы вычислить ошибку выборки при принятой доверительной вероятности, нужно рассчитать величину средней ошибки SK. Формула для ее определения (7.4) включает дисперсию признака в генеральной совокупности а2, которая, как правило, неизвестна. Может быть определена только выборочная дисперсия s2. Доказано, что соотношение между а и s определяется следующим равенством [c.169]
Рассмотрим пример. Для определения скорости расчетов с кредиторами предприятий одного треста была проведена случайная выборка 50 платежных документов, по которым средний срок перечисления денег оказался равен 28,2 дня со стандартным отклонением 5,4 дня. Определим средний срок прохождения всех платежей в течение данного года с доверительной вероятностью F(t) = 0,95. Тогда t = 1,96 скорректированная дисперсия [c.169]
Предельная ошибка выборочной доли с принятой доверительной вероятностью имеет вид [c.171]
Эта величина меньше предельной ошибки выборки, гарантированной с принятой доверительной вероятностью, 0,36 < 0,55. Следовательно, выборка репрезентативна по этому признаку. [c.177]
Соответствующая доверительная вероятность 0,899 (см. приложение, табл. 1). Вероятность того, что средний срок горения лампы меньше 1410 ч, равна [c.186]
Выборочные средние и относительные величины распространяются на генеральную совокупность обязательно с учетом предела их возможной ошибки. Приводится выборочный показатель со справкой о пределах ошибки с указанием доверительной вероятности х А., , р Д . Или же указывают границы значений генеральной характеристики с определенной вероятностью F(t) [c.187]
Как уже отмечалось, в случае малой выборки только для нормально распределенной генеральной совокупности могут быть рассчитаны и доверительные вероятности, и доверительные пределы генеральной средней. [c.191]
Если принять доверительную вероятность равной 0,954 и допустимую ошибку 0,005, т.е. 0,5%, то = — -------= 40 000 наблюдений. [c.220]
Если при проверке отобранных документов ошибок не обнаружено, то с принятой доверительной вероятностью мы можем распространить результаты выборки на всю генеральную совокупность и считать, что итог по генеральной совокупности не завышен более чем на величину предельно допустимой ошибки. Если же обнаружена по крайней мере одна ошибка, то первоначальная гипотеза относительно отсутствия ошибок, которая закладывалась при планировании выборки, оказывается несостоятельной. В этом случае должны быть пересмотрены либо значение коэффициента надежности, либо величина предельно допустимой ошибки (точность), либо и то, и другое. Если ошибки выявлены в операциях, значение которых превышает величину шага отбора, то можно быть уверенным в отношении аб- [c.223]
Как известно, в экономических исследованиях обычно принимают доверительную вероятность не ниже 90%. [c.225]
Для вычисления доверительных границ прогноза линии регрессии нужно умножить ее среднюю ошибку на /-критерий Стьюдента. При 14 степенях свободы и доверительной вероятности 0,95 (а = 0,05) значение /-критерия равно 2,14. Получаем доверительные границы 55,85 2,629 -2,14, или от 50,22 до 61,48 ц от 1 коровы. Интервал [c.252]
Величина доверительного интервала существенно зависит от объема выборки п (уменьшается с ростом и) и от значения доверительной вероятности у (увеличивается с приближением у к единице). [c.45]
Доверительный интервал для функции регрессии. Построим доверительный интервал для функции регрессии, т.е. для условного математического ожидания M Y), который с заданной надежностью (доверительной вероятностью) у = 1— а накрывает неизвестное значение Mx(Y). [c.64]
Полученные для выборочной совокупности НГДУ уравнения регрессии (20) — (22) могут точно не совпадать с истинной зависимостью, характерной для генеральной совокупности НГДУ. Поэтому необходимо найти доверительный интервал Д, в котором с определенной вероятностью будет находиться расчетная величина производительности труда. Для среднего значения производительности труда у величину доверительного интервала при заданной доверительной вероятности, являющейся минимальной, рассчитывают по формуле [c.89]
Эти и другие результаты примеров, помещенных в этой главе, можно получить, используя электронные таблицы Ex el. Достаточно ввести в таблицы данные, кнопкой мыши открыть Сервис -> Анализ данных -> Описательная статистика , установить уровень доверительной вероятности 95% и получить результаты среднее 538, отклонение 132. [c.62]
Теория малых выборок разработана английским статистиком В. Госсетом (писавшим под псевдонимом Стьюдент) в начале XX в. В 1908 г. им построено специальное распределение, которое позволяет и при малых выборках соотносить / и доверительную вероятность F(t). При п > 100 таблицы распределения Стьюдента дают те же результаты, что и таблицы интеграла вероятностей Лапласа, при 30 < п < 100 различия незначительны. Поэтому практически к малым выборкам относят выборки объемом менее 30 единиц (безусловно, большой считается выборка с объемом более 100 единиц). [c.190]
Выдвигается гипотеза о том, что норму выработки пересматривать не нужно, т.е. Н0 ц = 400 кг. Проверим эту гипотезу на 5%-ном уровне значимости. Критическое значение /-критерия определяется по таблице распределения Стьюдента при доверительной вероятности 0,95 (1 - 0,05) и числе степеней свободы d.f. = п - 1 = 8. Критическое значение составит (кршп= 2,3. Фактические значения /-критерия вычисляются по формуле (7.36) [c.209]
Если фактическая частота несоответствий в оформлении документов меньше максимально допустимой, то вычисляют коэффициент надежности как произведение объема выборки на величину фактической частоты несоответствий, посяе чего по таблице распределения Пуассона определяют вероятность, соответствующую рассчитанной величине коэффициента надежности, чтобы убедиться, что доверительная вероятность результатов выборки достаточно высока. [c.221]
Например, если аудитор исходит из 1%-ного риска (при односторонней критической области — опасения, что суммарная ошибка будет не больше принятой величины), т. е. при 98%-ной доверительной вероятности наличия суммарной ошибки 50 000 руб. при объеме генеральной совокупности, равном 60 млн/ руб., то объем выборки [c.222]
