Относительная погрешность топливораздаточных колонок [c.138]
Необходимая численность экспертов устанавливается в зависимости от допустимого уровня относительной погрешности (С) и коэффициента вариации выборки (V) [c.58]
X — среднеарифметическая величина экспертной оценки. Руководителем рабочей группы должна быть заранее установлена доверительная вероятность получения среднеарифметической выборочной экспертной оценки с относительной погрешностью не более С. Она обозначается буквой а. Обычно С принимается на уровне 0,1 V определяется по результатам пробного опроса экспертов, а доверительная вероятность невыхода С за установленные пределы а = 0,95 -ь 0.99. [c.59]
Коэффициент регрессии ff/= 22,4O4 этого уравнения найден с высокой точностью, превышающей табличное значение функции Стьюдента для уровня значимости 0, 9 9. Относительная погрешность приближения по этому уравнению колеблется от 0,5 до 5%. [c.50]
Если размеры залежи значительны, то можно оперировать вместо целых частей [а] самими числами а, так как относительная погрешность при этом будет невелика. Тогда приведенным выше соотношениям можно придать более компактный вид. [c.216]
У — относительная погрешность номинала Матрица планировании [c.147]
Пример. Предварительное исследование показало, что 10% покупателей предпочитают одну из нескольких моделей товара, т.е. вероятность их выбора, которая оценивается частостью, составляет 0,10. Определим размер выборки покупателей, которых надо опросить, чтобы оценить вероятность этого выбора с относительной погрешностью не более 5%. [c.67]
При значительных размерах залежи относительная погрешность при переходе от целых частей к самим числам невелика. Поэтому вышеприведенным отношениям можно придать более компактный вид [c.106]
Не нарушая общности, зададимся условно-фиксированными относительными погрешностями 6(- (6,- > 0) флуктуации количеств х (i = 1, т). Реализованное значение х при заданных относительных погрешностях 6 (. выражается дробью [c.137]
Если на осях координат нанесены логарифмические шкалы и, следовательно, построена логарифмическая сетка, то чаще всего можно достичь выпрямления различных кривых. Строя логарифмическую шкалу, получают одну и ту же относительную погрешность отсчетов по всей длине этой шкалы, построенная номограмма будет практически более удобной и точной при [c.166]
Исполнение Класс точности Относительная погрешность обработки [c.128]
Относительная погрешность в определении минимального значения Тц, с выявлялась по формуле [c.185]
Параметр "Относительная погрешность" служит для задания точности, [c.14]
Относительная погрешность" не позволяет найти оптимальное решение. [c.16]
Характеристикой класса является относительная погрешность, [c.164]
В отличие от задач прямого моделирования обратные задачи относятся к классу некорректных (в математическом смысле), в частности, неустойчивых относительно погрешности входных данных. Однако современное моделирование обладает средствами для их решения, что существенно расширяет возможности применения математического моделирования в экологии. [c.6]
При использовании динамических моделей экономики изучаются свойства различных Т. экономического развития. Среди них — устойчивость относительно погрешностей в начальных данных и относительно внешних воздействий вероятностный характер (в прогнозе и даже в плане может идти речь не о точно определенной единственно целесообразной Т., а о некотором множестве возможных Т. будущего развития примером могут служить известные из истории "вилки" показателей пятилетних планов). Следует различать оптимальность и эффективность Т. оптимальной называется Т., обеспечивающая на протяжении изучаемого периода лучшие результаты относительно заданного общего критерия качества системы, а эффективной — Т., которая оптимальна по некоторому подходящему частному критерию, так что эффективная Т. может не быть оптимальной, а оптимальная — всегда эффективна. [c.365]
При наличии погрешностей в измерениях оценки относительных погрешностей учитываются при проведении расчетов для отдельных горизонтов и дают возможность оценивать зависимость результатов от точности измерений. [c.141]
Исследование на точность метода проводилось для алгоритмов сдваивания с N = 8 при разрезании их на р = 4, 8 подграфов. Было проведено по 70 опытов для каждого случая. На рис. 1. 45 изображена функция распределения / относительной погрешности для этих двух случаев. [c.148]
| Рис. 1.45. Функция распределения / относительной погрешности 5 алгоритма А1 при разрезании графа сдваивания с п = 15 на 1) р = 4 2) р = 8 подграфов | 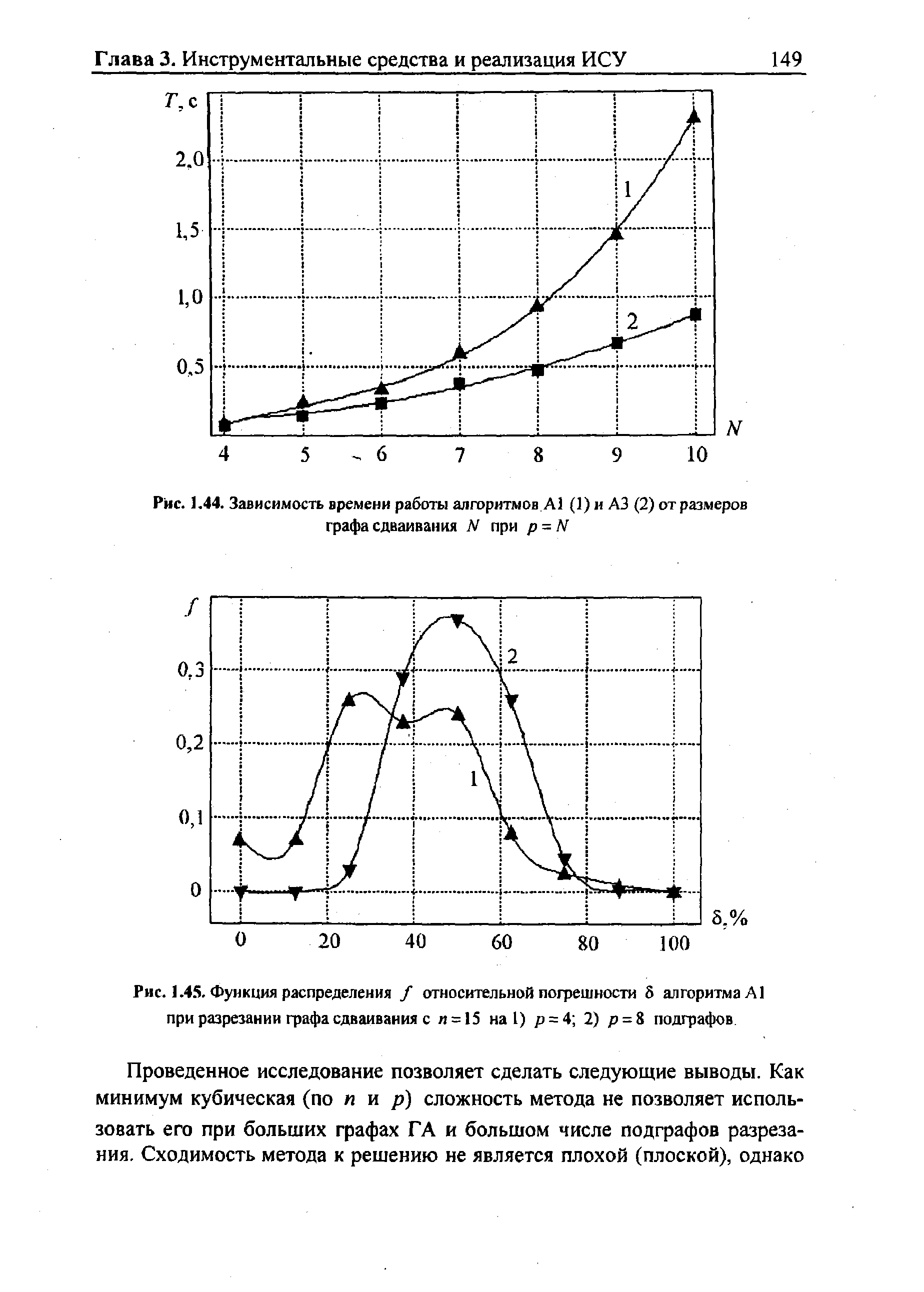 |
Кроме того, существуют почти вечные ресурсы. График рис. 2 показывает, что для г = 25% в год при сроке службы 15 лет цена практически не отличается от предельной. Так как 0.820 0.01, срок в 20 лет можно считать практически бесконечным , если нас устраивает относительная погрешность в 0.01 (с учетом неопределенности будущего нас устроил бы и более грубый результат). Нетрудно подсчитать, что при г = 10% в год практическая бесконечность наступит через 48 лет. Такие сроки службы не являются чрезмерно большими для зданий и многих сооружений, так что и они могут быть включены в число почти вечных ресурсов. [c.176]
Код Разность в классе точности или относительной погрешности измерения Рассогласование В1 уровне абсолютной погрешности [c.21]
В целом одна итерация по затратам времени соответствует, примерно, пятикратному интегрированию прямой системы. Заметим, что эта система (как и сопряженные) интегрировалась не с шагом сетки t = TjN, а с меньшим, обеспечивающим высокую точность вычисления значений xi (t). В [41] нет данных, которые позволили бы составить хоть какое-то представление о трудоемкости решения задачи методом локальных вариаций. Однако сравнение точности полученных решений можно произвести. В [41] найдено решение с / 0 = 169,42, ошибка 2,87 составляет 1,7% от jF0=166. В наших расчетах ошибка не превосходит О, 07, т. е. 0,04 %. В действительности относительная погрешность расчетов больше. Дело в том, что величина F0 состоит из двух частей [c.280]
Используя результаты [39, п. 37 257], запишем теперь следующие оценки сверху для относительных погрешностей решений центрированной системы (8.60") и нормальной системы (8.60" ) [c.274]
Легко видеть, что значение k 1 и оно возрастает, когда si убывает при фиксированном значении x . Для относительной погрешности оценок (8.67) и (8.6Г) верны следующие неравенства [c.278]
В некоторых ситуациях, например, когда объем данных велик, и они размещены во внешней памяти, желательно избежать двукратного считывания данных при вычислении элементов ковариационной матрицы. Для этого можно использовать оценки типа скользящего среднего, которые позволяют вычислять ковариационную матрицу с той же относительной погрешностью, что и двухэтапная оценка. Приведем один из возможных вариантов алгоритмов вычисления элементов а [259] [c.279]
Синхронность работы указателей 4,6 разового устройства и суммарного отпуска задающего устройства Относительная погрешность при но- 4,9 минальной производительности Относительная погрешность при 4,10 [c.138]
В настоящее время класс точности измерительной техники по основным технологическим автоматически регулируемым процессам достаточно высок и обеспечивает в большинстве случаев надежность определения входных, внутрисистемных и выходных параметров технологии в производственных условиях. При этом достигается большая согласованность в уровне относительной погрешности на входах и выходах систем автоматического регулирования, чем при функционировании локальных КИПиА. Уровень такой погрешности в основном соответствует размерности задач по контролю снижения потребления ресурсов в производстве и эффективности внедрения новой техники. При разработке систем автоматического регулирования и автоматизации производства большое значение имеет автоматизация контроля операций по приемке и отпуску важнейших видов ресурсов на припроизводственных и общезаводских сырьевых складах, а также при определении количества и параметров электрической энергии и природного газа. [c.20]
Опыт совершенствования контроля производства в Гродненском производственном объединении Азот , Воскресенском Минудобрения , Северодонецком Азот , Апатит , Полимир и др. показывает, что окупаемость затрат на улучшение контроля производства целесообразно рассчитывать по его видам (физический, химический, металлографический и др.) и стадиям (входной, внутрипроизводственный и выходной). Наиболее точно эффективность мероприятий по улучшению контроля производства определяют прямым счетом по показателям сокращения погрешности измерения. В расчетах целесообразно использовать показатель снижения относительной погрешности измерения. Для определения срока окупаемости по методу прямого счета сначала рассчитывают потенциальную экономическую эффективность мероприятий по уменьшению относительной погрешности измерений (Эп) [c.23]
Срок окупаемости мероприятий по улучшению контроля можно рассчитать сопоставлением разовых затрат на них со стоимостью дополнительного количества сырья и материалов, получаемого от поставщиков вследствие уменьшения недозагруз-ки, и дополнительной прибылью, которая получена (или может быть получена) в результате выпуска продукции из этих ресурсов. Умножением размера снижения относительной погрешности контроля на объем потребления "материала определяют стоимость дополнительно получаемого предприятием количества ресурсов за весь период действия мероприятия. Для определения экономического эффекта от мероприятий по совершенствованию метрологического обеспечения за отчетный период из расчетной экономии вычитают разовые затраты. Размер последних принимают, исходя из предполагаемого срока службы новых типов контрольно-измерительной и лабораторной техники. [c.152]
Но уравнение для х1 в силу Аг—0 очень просто, и из условий х1 (Т)=0 и и1 (t) 0 следует, что первое слагаемое (144) будет найдено точно, какой бы ни была функция и1 (t) (а в данной задаче имеется семейство решений, дающих одно и то же минимальное значение F0, так что и1 (t) определяется с большой степенью неопределенности). Таким образом, вся ошибка численного решения связана с ошибкой во втором слагаемом, и относительная погрешность в нем составляет 12,5% для метода локальных вариаций и 0,3% в наших расчетах. В [41 ], [86] исходная траектория характеризуется как точка локального минимума вариационной задачи. Это, как показали наши расчеты, неверно. Легко проверить (предоставим это читателю), что исходная траектория является стационарной точкой метода локальных вариаций принятая в этом методе техника варьирования траектории действительно не приводит к изменению значения функционала. Но это есть следствие дефекта метода, а не особенность данной траектории. Ведь если бы мы имели дело с локальным минимумом задачи, то и наш метод не позволил бы эту траекторию проварьировать как и всякий реализуемый метод, он является методом поиска лишь локального минимума. Поэтому замену функционала (2) на функционал [c.280]
