Пример 4. Графики на координатах с логарифмической шкалой. Логарифмическая шкала на осях координат строится по принципу построения логарифмической линейки. [c.175]
На фьючерсных рынках буквально все графики, которые можно приобрести через коммерческие информационные службы, используют арифметическую ценовую шкалу. Однако для некоторых видов анализа, особенно если речь идет об анализе долгосрочных тенденций, удобно пользоваться шкалой логарифмической (см. рис. 3.6 и 3.7). На рисунке 3.6 изображены арифметическая и логарифмическая шкалы, так что разница между ними сразу бросается в глаза. Если мы возьмем арифметическую шкалу, то расстояния между делениями у нее неизменны. На арифметической ценовой шкале движение с отметки 5 до отметки 10 по расстоянию будет равно движению с отметки 50 до отметки 55. Расстояние будет одно и то же, хотя в первом случае это означало, что цена возрастала вдвое, а во втором -лишь на 10%. Если же мы пользуемся логарифмической шкалой или, как ее еще называют, процентной шкалой, то тут одинаковое расстояние на шкале соответствует одинаковым в процентном отношении изменениям. Например, от отметки 10 до отметки 20 (возрастание цены на 100%) расстояние такое же, как от 20 до 40 или от 40 до 80. Следует обратить внимание на то, что все деления [c.57]
В системе прямоугольных координат с логарифмическими шкалами функции снижения трудоемкости [см. формулу (10.1)] представляют прямые линии, тангенс угла наклона которых соответствует показателю степени Ь, так как [c.96]
Иногда при больших изменениях показателя прибегают к логарифмической шкале. Предположим, значения показателя изменяются от I до 100 (в 100 раз) это может вызвать затруднения при построении графика. Если перейти к логарифмам, то их значения для минимальных-максимальных значений показателя будут различаться не так сильно log 1 = 0, log 100 = 2. [c.66]
Доллары, логарифмическая шкала [c.38]
Прибыли на 1 инвестированный доллар (логарифмическая шкала) [c.911]
График. Строится стандартный график по оси X откладывается величина финансового вклада в покрытие затрат, по оси Y — объем продаж. В зависимости от характера данных можно воспользоваться логарифмическими шкалами. [c.47]
Если на осях координат нанесены логарифмические шкалы и, следовательно, построена логарифмическая сетка, то чаще всего можно достичь выпрямления различных кривых. Строя логарифмическую шкалу, получают одну и ту же относительную погрешность отсчетов по всей длине этой шкалы, построенная номограмма будет практически более удобной и точной при [c.166]
Переход от заданного уравнения к уравнению логарифмической шкалы осуществляется путем разделения переменных, сущность которого заключается в том, что уравнение [c.167]
При построении семейства по х имеем р = —0,414, со = 0,4.. Следовательно, при модуле логарифмической шкалы сетки К, модуль шкалы параметра х равен [c.169]
Знак минус означает, что возрастание численных, значений пометок логарифмической шкалы семейства по х идет сверху вниз. [c.169]
Прежде чем начать строить номограмму, нужно выяснить, какой из вариантов дает наиболее точные отсчеты и будет наиболее удобен для использования. Вычислять координаты точек для построения каждой линии семейства параллельных прямых необязательно. Достаточно построить одну наклонную прямую, вычислить модуль логарифмической шкалы семейства параллельных линий параметра и на нормали к построенной наклонной прямой построить шкалу этого модуля. Пользуясь шаблоном логарифмических шкал разных модулей, наносим штрихи этой шкалы, учитывая приведенное выше правило определения направления повышения пометок. Затем через штрихи проводим прямые, параллельные наклонной прямой, и на них подписываем значения параметров. [c.173]
Для величины потенциальных ресурсов можно указать математическое ожидание и доверительный интервал, который на логарифмической шкале задает интервал 6 а нормального закона распределения. Указанным приемом рассчитывались параметры логнормального закона распределения потенциальных ресурсов НГО I— IV (табл. 22). [c.204]
Добавив на логарифмическую шкалу несколько лет движения цены, вы можете устранить тренды и выделить только Сезонную Тенденцию каждого товара или акции. Данную Сезонную Тенденцию можно применять вместе с анализом Волны Эллиота, что поможет с распределением во времени различных составляющих Расчётов по Волне. [c.67]
Многие инвесторы удивляются использованию логарифмической шкалы для "крестиков-ноликов". Простым ответом будет то, что важен момент активного изменения цены на рынке. Трейдеры в биржевой яме, в Чикаго, не нуждаются в логарифмической шкале потому, что цены, которые они отслеживают, меняются незначительно в течение дня. Чтобы представить себе как бумага будет вести себя в течение следующих 6-18-ти месяцев, инвестор должен тщательно и рутинно просмотреть историю котировок за последние три года. Для акций часто характерно удвоение, утроение и т.п. цены за этот период. Логарифмическая шкала необходима, чтобы обеспечивать отображение данных на математически аккуратном масштабе. Представим себе момент, когда индекс Доу-Джонса, в один жестокий день медвежьего рынка потерял 500 пунктов, в 1974 году. Тогда эти 500 пунктов являлись падением индекса на 50%. Теперь, когда индекс больше 10000, падение на 500 пунктов, уже не равно 30%. [c.83]
Существует два недостатка использования логарифмической шкалы. Первый - значения шкалы в крайних точках не являются удобными круглыми числами. А второй заключается в исключительном неудобстве рисования таких шкал вручную. Да, мы вынуждены согласиться со старыми авторитетами, что нарисованный вручную график значит для трейдера гораздо больше, чем увиденный на экране. Однако, компьютер значительно облегчает слежение за сотнями бумаг, а ценность использования исторических данных перевешивает все возможные недостатки. [c.83]
АРИФМЕТИЧЕСКАЯ И ЛОГАРИФМИЧЕСКАЯ ШКАЛЫ [c.43]
Pu . 3. 6 Сопоставление арифметической и логарифмической шкал. Обратите внимание на то, что левая шкала имеет равные деления по всей протяженности, тогда как правая (логарифмическая) отражает процентные изменения. [c.43]
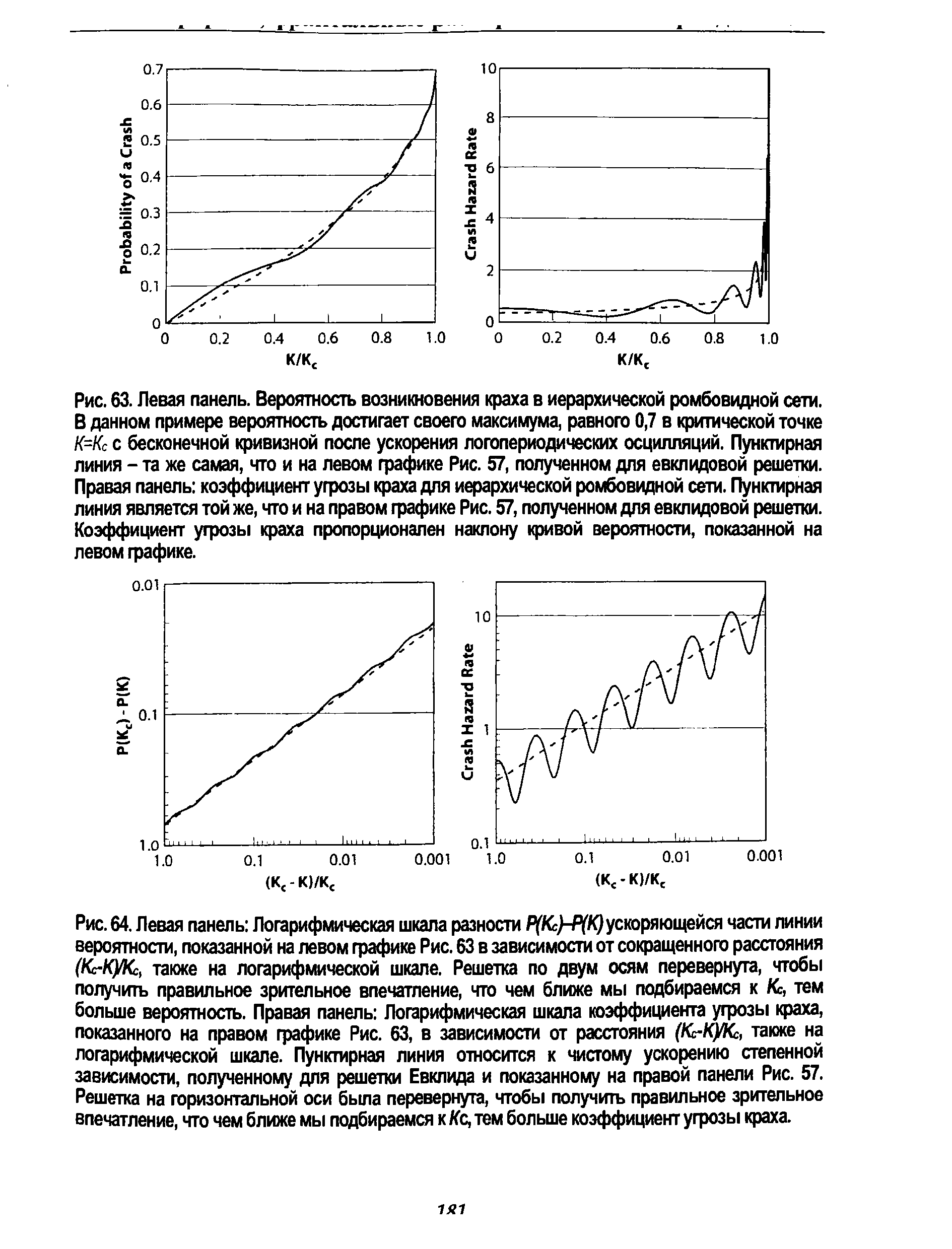
| Рис. 3.7 На этом рисунке представлены два графика по меди - месячный и недельный. Они составлены с использованием логарифмической шкалы. Обратите внимание, как деления становятся тем шире, чем ниже цены, и, напротив, становятся тем уже, чем цены выше. Вычерчивание линий тренда и канала может очень выиграть от использования логарифмической шкалы, особенно если речь идет о долгосрочных графиках. | 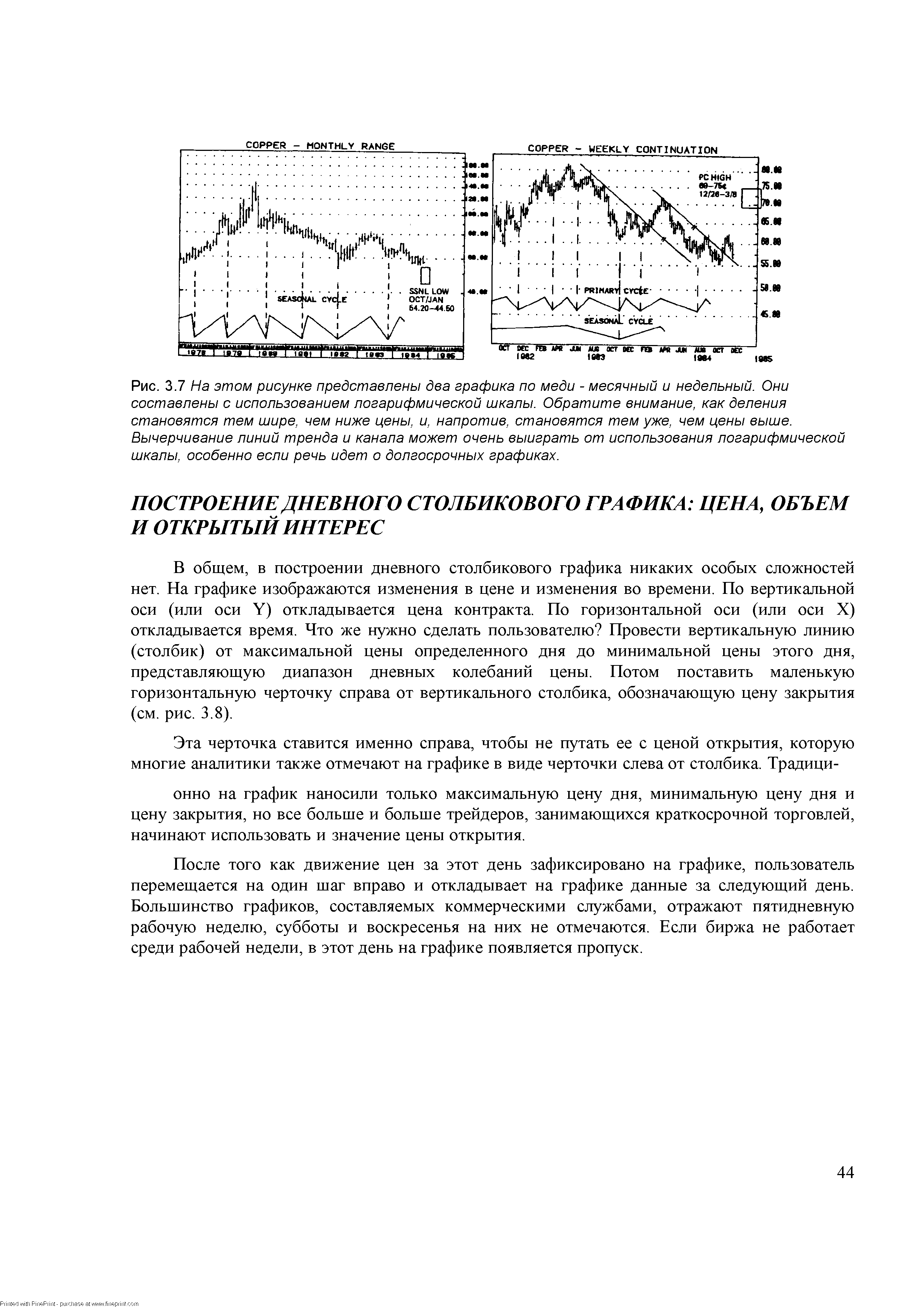 |
По оси изменения цен может использоваться как арифметическая, так и логарифмическая шкала. Употребление той или иной шкалы зависит от цели нашего анализа. Для цен мы будем брать лишь арифметическую шкалу как более простую и понятную. В техническом анализе логарифмическая шкала практически не применяется. Она интересна тем, что показывает не только направление изменения цен, но и скорость этого изменения. [c.86]
Чем дальше, тем сильнее в такой ситуации люди будут стремиться получить такую счетную единицу, изменение ценности которой было бы более тесно увязано с общей тенденцией, и даже, быть может, вынуждены будут использовать в качестве счетной единицы что-то такое, что нельзя использовать в качестве средства обмена. (Кривая, представляющая дисперсию изменений цен в виде доли всех продаж, произведенных за определенный период по возросшим или снизившимся по сравнению с предыдущим периодом ценам, будучи построена по логарифмической шкале, должна, конечно, иметь одну и ту же форму, независимо от того, используем мы в качестве измерителя цен деньги или какой-нибудь товар. Если мы используем в качестве стандарта товар, цена которого упала больше, чем цена любого другого, все изменения цен будут выглядеть как повышения, однако рост относительной цены одного товара по сравнению с другим будет оставаться одним и тем же, скажем, 50 процентов, какую бы систему мер, мы ни выбрали. Мы, вероятно, получим кривую в виде нормальной (гауссовой) кривой распределения ошибок. Случайные отклонения от нее в ту или другую сторону, насколько мы способны предсказать, будут взаимно погашаться, и количество их будет уменьшаться с ростом величины отклонения. (Большинство ценовых изменений будет вызываться смещением спроса с соответствующим падением некоторых цен и повышением других относительно мелкие смещения такого рода будут, вероятно, более частыми, чем крупные.) Общий уровень цен, выраженный в деньгах со стабильной в данном смысле ценностью и представленный данной кривой, не должен в этом случае меняться, а объемы сделок, совершаемых по ценам, возросшим или упавшим на некоторый процент, должны уравновешивать друг друга. Это минимизирует ошибки - не обязательно отдельных индивидуумов, но всего общества в целом. И хотя никакое индексное число, обычно исчисляемое для этих целей, не поможет полностью подтвердить то, что мы предположили, достаточно точное приближение к измерению такого эффекта вполне достижимо.) [c.61]
Пункт 3 табл. 3.1 указывает на то, какая шкала — арифметическая или логарифмическая (процентная) используется для построения того или иного типа графика (рис. 3.2). Арифметическая шкала наиболее проста и естественна и используется в большинстве случаев. Логарифмическая же шкала наглядно отражает не абсолютное изменение цены, а относительное и может быть полезна при составлении среднесрочного и долгосрочного графиков. [c.34]
Если нормативная зависимость имеет характер степенной функции вида у = Ъх а, где а Ф % графическое построение выполняется в координатах с логарифмическими шкалами, так как в этом случае нормативная зависимость аппроксимируется прямой линией. [c.213]
Если в интервальной шкале масштаб зафиксирован, то измерение происходит в шкале разностей. Шкала разностей допускает операции равенство-неравенство , больше-меньше , равенство-неравенство интервалов и операцию вычитания, на основе которой устанавливается величина интервала в фиксированном масштабе. К шкале разностей относятся логарифмические шкалы, а также процентные и аналогичные им шкалы измерений, задающие безразмерные величины. Например, указание года рождения — это представление возраста в шкале разностей. [c.28]
Цены обычно изменяются по мере прохождения продуктом стадий своего жизненного цикла (рис. 12.7). Из рис. 12.7 вытекает, что по мере увеличения объема продаж (выпуска продукта) и использования опыта обучения снижается себестоимость (в логарифмической шкале это изменение имеет прямолинейный характер). В период первоначального появления продукта на рынке, когда еще может продолжаться его маркетинговая разработка, а продукт еще плохо известен потребителю, возможно несение убытков. Далее, на этапе развитого спроса, цены могут расти, оставаться без изменения или даже, как изображено на рис. 12.7, слегка падать. В любом случае — это самый прибыльный этап. Далее, вследствие насыщения рынка, появления новых продуктов и усиления конкурентной борьбы, на этапах насыщения и спада возможно достаточно резкое снижение цены, но не ниже в общем случае некоего минимального уровня рентабельности по прибыли (линии цены и себестоимости идут параллельно). Как только условие сохранения минимального уровня рентабельности не выполняется, а для поддержания спроса необходимо более резкое снижение цены, относительно судьбы продукта на рынке принимаются другие, не ценовые, решения. [c.344]
Строится стандартный график по оси X откладывается величина финансового вклада в покрытие затрат, по оси Y — объем продаж. В зависимости от разброса данных можно использовать логарифмические шкалы, но, как правило, хватает обычного графика, где по осям напрямую откладываются значения параметров. [c.46]
Общий смысл модели B G состоит в том, что на оси абсцисс показаны оценки некоторых конкурентных позиций фирмы в данном бизнесе в виде отношения объема продаж фирмы в данной области бизнеса к объему продаж крупнейшего в данной области конкурента фирмы. В оригинальной версии B G шкала абсцисс является логарифмической. [c.173]
Ось абсцисс, как уже отмечалось, является логарифмической (если в логарифмических координатах отобразить зависимость между издержками на производство единицы продукции и объемом производства, установленную экспериментальным путем B G, то полученная функция будет иметь вид прямой линии). Поэтому обычно коэффициент, характеризующий относительную долю рынка, занимаемую бизнес-областью, изменяется от 0,1 до 10. Отображение конкурентной позиции (которая понимается здесь как отношение объема продаж фирмы в соответствующей бизнес-области к общему объему продаж у ее конкурентов) на логарифмической шкале является принципиальной деталью модели B G. Дело в том, что основная идея этой модели предполагает наличие такой функциональной зависимости между объемом производства и себестоимостью единицы продукции, которая на логарифмической шкале выглядит как прямая линия. [c.175]
Проф. А. Р. Ржаницын рекомендует [47] для несимметричных законов исправлять кривую Гаусса путем преобразования основной шкалы в логарифмическую [c.77]
Построение скользящей средней на диаграмме "крестики-нолики" более сложный процесс, чем на обычном столбцовом графике. Поэтому скользящие средние редко использовались с этим типом диаграмм. При появлении программного обеспечения технического анализа в 1980-х и, по мере его бурного развития в 1990-х, использование "крестиков-ноликов" было затруднено, в силу отличных требований к исходным данным. Компания UST Se urities orp. компьютеризовала их использование, ввела в обиход логарифмические шкалы, индивидуальные размеры ячеек и скользящие средние. [c.74]
Рассмотрим, например как располагаются на построенной карте банки разных размеров (см. Рисунок 10)а. Размеры банков берутся в логарифмической шкале причем клетки, отличающиеся на одну цветовую градацию, содержат банки с пятикратным отношением активов. Напомним, что величин активов банков была изначально выведена из набора параметров, т.к. она использовалась для нормировки остальных статей. Несмотря на это, банки разных размеров располагаются не хаотично, а регулярным образом, что свидетельствует о значимости размера банка при выборе им своей финансовой стратегии. Визуально на карте можно выделить следующие большие группы банков большие банки (низ карты), малые банки (группа слева и группа справа) и средние банки. Раскраска, отражающая относительный размер Уставного фонда показывает, что между двумя группами малых банков имеются существенные различия Банкмв нижнем правом углу карты практически не растут (Рисунок 11). [c.195]
Теория волн обеспечивает аналитика прогностическим инструментарием, наилучшим образом приспособленным к логарифмической шкале. Более того, ее фрактальная структура учитывает динамику развития экономических явлений. Фракталы - одно из понятий относительно новой, активно развивающейся Теории Хаоса (S ien e of haos), проблематика которой включает в себя явление турбулентности и сложную геометрию развития в природе. Гибкость и структурное единообразие Теории волн ассоциируется с фрактальной геометрией. Фигуры Эллиота повторяются снова и снова, каждый раз с небольшими вариациями затем они объединяются в фигуры больших масштабов, схожих с меньшими по форме, внешнему виду. Например, если исследовать Рисунок 1а под микроскопом, в длинном центральном сегменте [c.318]
| Рис. 11. Месячные котировки DJIA обратно экстраполированы от сентября 2000 года до января 1790 года. На вертикальной оси используется логарифмическая шкала, так что умножение на константу, например 10, соответствует добавлению на графике фиксированной константы. Математически, это означает переход от умножения к сложению и обеспечивает графическое сравнение графиков цен, когда они изменялись в разных пределах, различающихся в тысячи раз (в нашем случае от значения 3 в 1790 году до значений, больших 10000 в 2000). Толстая (и, соответственно, тонкая) непрерывные линии соответствуют экспоненциальному росту первоначальных инвестиций в 1 в 1790 г. (тонкая - в 1880 г.) с годовой нормой дохода около 2.9% (тонкая - 6.8%), которые превратились бы в 1000 (соответственно, 10000) в 2020 г. | 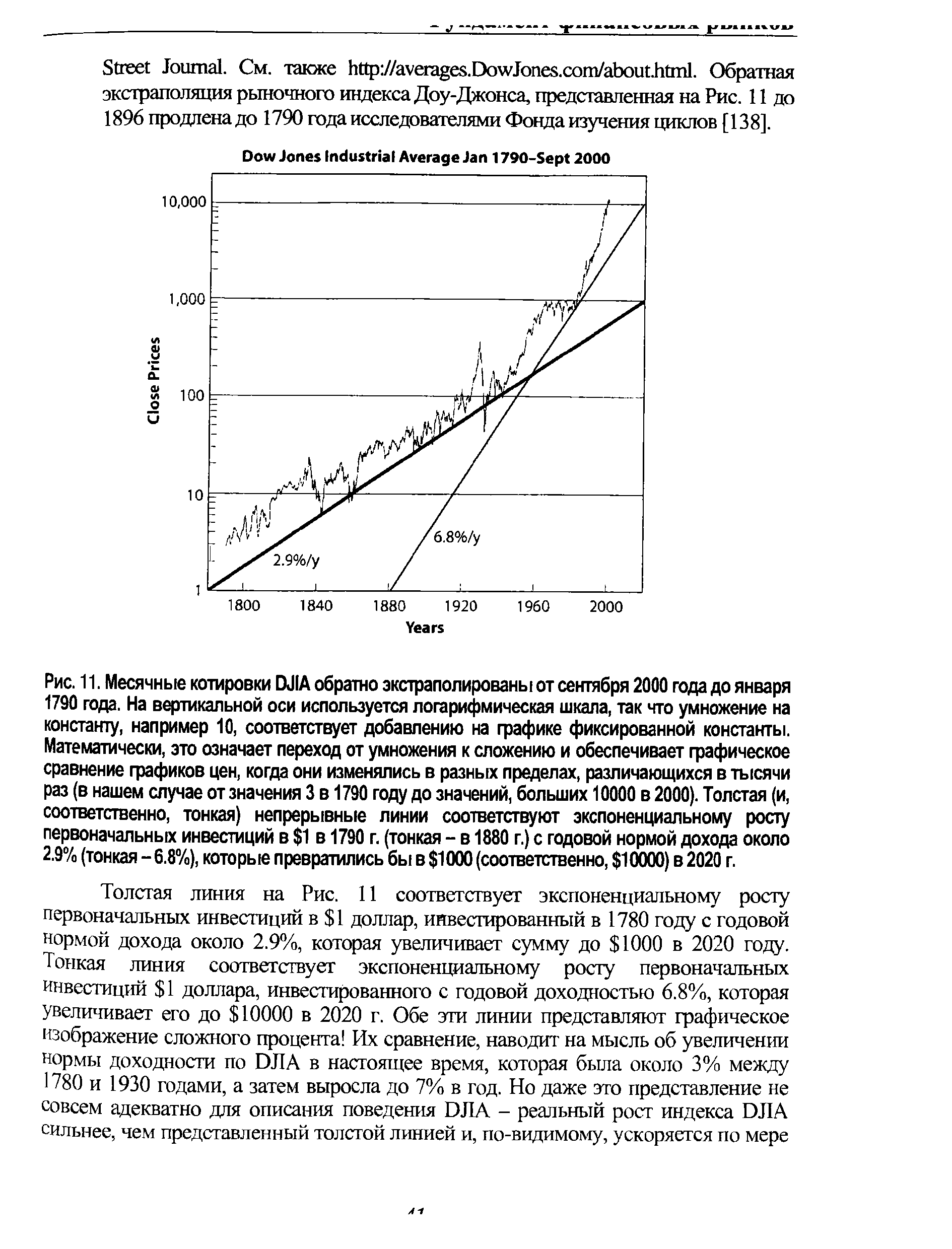 |
[c.187]
Предположим, что анализ некоторых данных показывает наличие логопериодических структур. Что мы можем из этого извлечь Прежде всего, как мы увидели, период логопериодичности на логарифмической шкале прямо связан с существованием предпочтительного коэффициента масштабирования. Таким образом, логопериодичность должна быть немедленно замечена и истолкована как существование множества предпочтительных характеристических масштабов, вместе формирующих геометрический ряд. .Jf, X1 1,. ..J, J ,., .,. А",... Логопериодические структуры в данных, таким образом, указывают, что система и/или подлежащие физические механизмы обладают характеристическими масштабами, каждый из которых характеризуется соответствующим размером. Это крайне интересно, поскольку существенно ограничивает лежащий в основе этого механизм. Действительно, поведения с простой степенной зависимостью обнаруживаются повсеместно, как видно из бурного роста концепций фракталов, критичности и самоорганизующейся критичности [26]. Например, степенное распределение энергии землетрясений, известное как закон Гетенберга-Рихтера, может быть получено при помощи многих различных механизмов и описано множеством моделей и, таким образом, крайне ограничено в выявлении лежащей в его основе физики (один факт, много конкурирующих объяснений). Его полезность как модельных представлений даже подвергается сомнению, что противоречит общей уверенности, свойственной многим ученым, в важности этой степенной зависимости. Напротив, присутствие логопериодических свойств учит нас тому, что существуют важные физические структуры, скрытые в полностью инвариантном описании. [c.209]
Ось ординат шкала цены иногда логарифмическая ческая, редко логариф- Арифметическая Арифметическая [c.33]