Уравнение Лапласа - Гаусса предполагает непрерывное изменение / и неограниченное возрастание п. Поэтому площадь нормальной кривой, заключенную между ординатами /, и t2, определяют, интегрируя функцию (7.7). [c.168]
Ее фафик — колоколообразная кривая Гаусса, имеющая максимум в точке F= mF, представленная на рис. 10.5. [c.214]
| Рис. 10.5. Кривая нормального распределения Гаусса для значений функций долевого участия собственных средств | 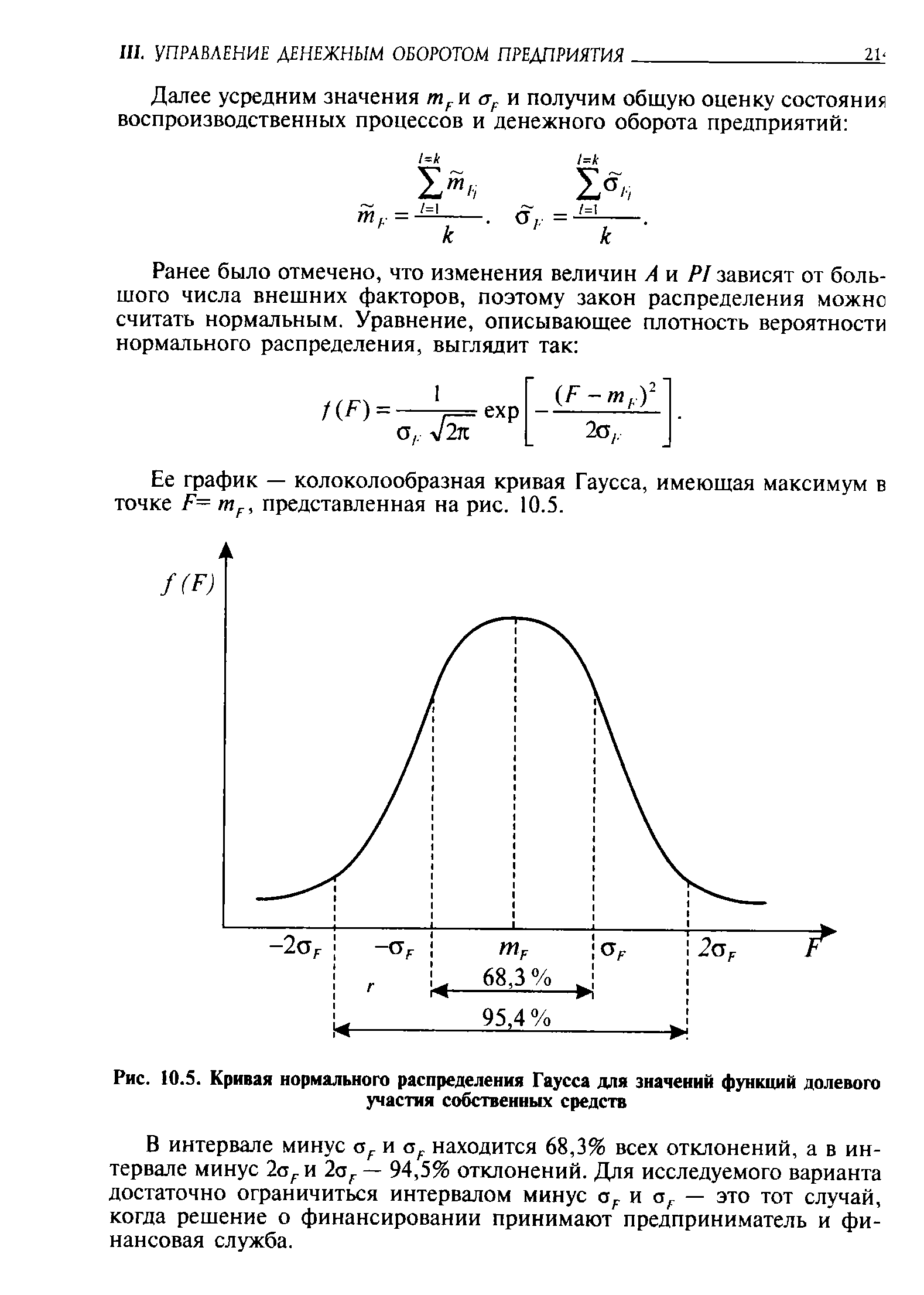 |
Наиболее распространены статистические методы предупредительного контроля, основывающиеся на законе нормального распределения, характеризующегося известной кривой Гаусса. [c.155]
Наиболее распространенной теоретической кривой, описывающей симметричное распределение, является кривая Гаусса, называемая также нормальной кривой (фиг. 27). Ее уравнение [c.77]
По существу, кривая Гаусса соответствует только симметричным распределениям. Однако она может быть получена и как предельная кривая, к которой стремятся прочие кривые распределения по мере беспредельного возрастания числа независимых обстоятельств, от которых зависят наблюдаемые явления. [c.77]
Вместо исправления кривой Гаусса можно непосредственно применять несимметричные кривые распределения (Пуассона, Пирсона и др.). [c.78]
Поэтому, чтобы подобрать нормальную кривую Гаусса, необходимо [c.79]
Распределение имеет вид симметричной колоколообразной кривой, распространяющейся по всей числовой оси. Распределение Гаусса зависит от двух параметров (//, сг). [c.34]
Единственная переменная величина в методе фиксированных пропорций называется дельта. Эта переменная просто обеспечивает математическую формулировку метода, а также определяет, насколько агрессивно или консервативно следует вести управление. Чем меньше значение переменной, тем более агрессивным должно быть управление ресурсами. Чем больше величина переменной, тем более консервативно управление. Кривая Гаусса в Фиксированно-Пропорциональном методе не используется. [c.89]
В качестве меры крутости графи ков распределения случайных величин используют коэффициент эксцесса Ek, характеризующий крутость графика по сравнению с кривой Гаусса. Для оценки Ek [c.48]
По мере удаления от точки fl плотность распределения уменьшается. Максимальная ордината кривой распределения обратно пропорциональна О. Площадь под кривой Гаусса равна 1 или 100% всех значений случайной величины в генеральной совокупности. [c.160]
Идея информационного метода определения закона распределения заключается в следующем. Так как оценка энтропии распределена по закону Гаусса, то гипотеза о совпадении эмпирического и предполагаемого теоретического распределения принимается, если вычисленное по результатам экспериментальных данных значение Я (х) будет находиться в пределах доверительного интервала кривой нормального распределения с параметрами М[Н] и >[Я]. Нормированная по среднеквадратическому отклоне- [c.28]
Внимательное изучение данных на Рисунке 9.1 показывает профили продолжительности жизни этих двух индексов демонстрируют распределение по правильной кривой Гаусса распределения S P 500 или любого другого главного индекса коррелируют с подобной последовательностью, то есть движения рынка действительно имеют тенденцию ограничиваться статистически предсказуемой продолжительностью жизни. [c.157]
Инвесторы всегда хотят владеть самыми выгодными при данной цене акциями. Ожидаемый доход от портфеля таких акций равен математическому ожиданию, или среднему от ожидаемого дохода отдельных пакетов акций, входящих в портфель. Но пакеты, обещающие наибольшие прибыли, часто приносят разочарование, тогда как другие превосходят самые оптимистичные прогнозы. Марковиц предположил, что распределение вероятностей значения доходности портфеля вокруг ее математического ожидания описывается симметричной нормальной кривой Гаусса. [c.365]
График функции нормального распределения описывается, так называемой, нормальной кривой (кривой Гаусса — рис. 3.1.) [c.47]
График функции f(t) плотности распределения нормального закона называется нормальной кривой или кривой Гаусса. [c.115]
Наиболее известным и, наверное, наиболее распространенным в практической деятельности является нормальное распределение, иногда называемое распределением Гаусса. Данный вид распределения часто встречается в природе. Например, закону нормального распределения подчиняется случайная выборка людей по росту, весу и даже интеллектуальному развитию. Выглядит нормальное распределение как симметричная колоколообразная кривая. Среднеарифметическая ряда, подчиняющегося закону нормального распределения, равна моде и медиане этого ряда. [c.185]
Это позволяет описывать кривой Гаусса и несколько несимметричные опытные кривые, предполагая, что они по мере увеличения числа наблюдений выравниваются. Если отклонения от симметрии значительны, то возможно исправление кривой Гаусса введением так называемой пертурбационной функции, в виде многочлена не выше четвертой степени. Эту же кривую можно представить в виде ряда по производным нормального закона Гаусса (ряд Грамма — Шарлье типа А). [c.77]
Проф. А. Р. Ржаницын рекомендует [47] для несимметричных законов исправлять кривую Гаусса путем преобразования основной шкалы в логарифмическую [c.77]
В нормальной кривой асимметрия и эксцесс равны нулю, а куртозис равен трем. Эти данные могут служить дополнительными признаками соответствия эмпирического материала нормальному закону Гаусса. [c.79]
Концепция случайных блужданий проста, но богата своими приложениями не только в финансах, но и в физике, и в описании естественных процессов. Бесспорно, это одна из наиболее важных фундаментальных концепций, как в современной физике, так и в современных финансах, как являющаяся основанием теории элементарных частиц, представляющих собой строительные блоки Вселенной, так и описывающая сложные процессы вокруг нас. В простейшей вы бросаете монету, в результате чего двигаетесь вверх, если выпал "орел" или вниз -если выпала "решка". Где вы окажетесь после множественного повторения таких подбрасываний Ответ на поставленный вопрос многозначен в среднем вы остаетесь в той же самой позиции, так как среднее от одного шага вверх и одного шага вниз эквивалентно отсутствию какого-либо движения. Однако, ясно, что существуют флуктуации вокруг этого нулевого среднего значения, которые увеличиваются с увеличением числа подбрасываний. На Рис. 19 представлена траектория синтетически случайной рыночной цены, смоделированная компьютером, для определения конечного ценового сдвига в результате многократного изменения "цен". В данном случае, шаг или приращение имеет случайный "знак", а амплитуды приращений последовательных распределены согласно так называемому закону распределения Гаусса, графически изображаемого в виде хорошо известной колоколообразной кривой. [c.51]
Интерес Г. Беккера к религии, возможно, обусловлен тем, что на банкнотах долларов США есть надпись "In God We Trust" ("Мы верим в Бога"). Несмотря на этот лозунг, количество финансовых афер в США больше, чем во многих других странах [Известия. 2001. 16 июня. С. 5]. На банкнотах немецкой марки (DM) нет любимого лозунга солдат третьего рейха "Gott mit uns" ("С нами Бог"). Такую надпись можно увидеть в" кирхах Германии, а на бумажных деньгах этой страны помещены портреты ГеТе, Лейбница, Гаусса и других деятелей немецкой культуры. Купюру в 10 DM украшает портрет великого математикачКарла Фридриха Гаусса на фоне кривой нормального закона распределения вероятностей. Хочется надеяться, что огда-нибудь на российских десятирублевках появятся портреты Пушкина на фоне лукоморья с зеленым дубом, золотой цепью и ученым котом. [c.258]
Генерировалась последовательность псевдослучайных чисел с распределением Гаусса. Использовался универсальный алгоритм, основанный на учете формы кривой плотности распределения [12]. В качестве датчика равномерно распределенных чисел использовался генератор URAND [100]. [c.55]
Другая математическая проблема заключалась в том, что портфели и сами рынки ценных бумаг описывались только двумя числами — ожидаемой доходностью и дисперсией. Зависимость именно от этих двух чисел оправданна, только если доходность ценных бумаг описывается кривой Гаусса. Отклонения от нормальной кривой недопустимы, и множество значений с каждой стороны от среднего должно быть распределено строго симметрично. [c.462]
Поток с ограниченным последействием поток Пальма поток Эрланга k-то порядка закон распределения Эрланга k-то порядка с параметром Я нормированный поток Эрланга k-то порядка центральная предельная теорема для одинаково распределенных слагаемых случайных величин сходимость по вероятности мера последействия нормальное распределение нормальная кривая кривая Гаусса Гаусс К.Ф. Чебышёв П.Л. [c.121]
